「分块」学习笔记

「分块」

算法思想

当我们对于一个很大数组 ((1e5)) 进行区间修改和区间查询时，我们会想到线段树的 (nlog_n) 的优秀效率。

分块——优雅的暴力！！！

我们将区间分成每个大小为 (S) 的小块，这样我们的复杂度就会从 (n) 降到 (frac n S) 的效率。

基本思路

初始化

我们先将数组分成长度为 (S) 小块，用原下标除以 (S) 向上取整，就是他分块后的小块标号。

void Init() { //分块初始化
	S = sqrt(n);
	for (register int i = 1; i <= n; i ++) {
		bel[i] = (i - 1) / S + 1; //向上取整
		size[bel[i]] ++; //统计每个块的大小，为什么不直接L[i] - R[i]，因为可能最后一个块的大小不是S
		sum[bel[i]] += a[i]; //统计每个块的权值总和
		if (!L[bel[i]]) L[bel[i]] = i; //每个块的左端点
		R[bel[i]] = i; //每个块的右端点
	}
}

区间修改

若我们要将 (l) 到 (r) 的区间内都加上权值 (w)。

若这个区间在一个小块里面

直接 (S) 的效率一个一个修改即可。

若这个区间横跨了多个小块

如下图

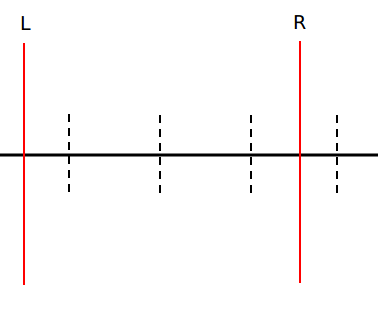
我们先用 (S) 效率将左右两端无法组成一个块的单点都加上。

然后对于中间的块，一个一个块都打上标记，跟线段树上的标记差不多，最后区间查询时加上即可。

void Modify(int l, int r, int w) { //区间修改
	if (bel[l] == bel[r]) { //如果这个区间在同一个块里
		sum[bel[l]] += (r - l + 1) * w; //块的值加上
		for (register int i = l; i <= r; i ++) { //每个单点的值也加上
			a[i] += w;
		}
	}else {
		Modify (l, R[bel[l]], w); //最左边无法组成一个块的
		Modify (L[bel[r]], r, w); //最右边无法组成一个块的
		for (register int i = bel[l] + 1; i < bel[r]; i ++) { //把中间的块加上，并打上花火 &!@*^$&*^*&^@
			tag[i] += w;
			sum[i] += size[i] * w;
		}
	}
}

区间查询

跟区间修改的思想类似

若这个区间在一个小块里面

将这个块里标记值加上，在加上单点的值即可。

若这个区间横跨了多个小块

将无法组成左右无法组成一个小块的部分用上面的思路加和。

剩下的一块一块直接加上 (sum[i]) 即可。

inline int Query(int l, int r) { //区间查询
	int ans = 0;
	if (bel[l] == bel[r]) {
		ans += (r - l + 1) * tag[bel[l]]; //把之前整块修改的值加上
		for (register int i = l; i <= r; i ++) { // 把之前单点修改后的值加上
			ans += a[i];
		}
	}else {
		ans += Query(l, R[bel[l]]); //最左边无法组成块的值加上
		ans += Query(L[bel[r]], r); //最右边无法组成块的值加上
		for (register int i = bel[l] + 1; i < bel[r]; i ++) {
			ans += sum[i]; //这样我们的sum数组就可以直接查了
		}
	}
	return ans;
}

时间效率

自我感觉比线段树好写，而且在某些题上会比线段树跑得快。

例如这个板子题

分块

线段树

练习题

打一波广告

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;

inline int read(){
	int x = 0, w = 1;
	char ch;
	for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * w;
}

int n, m, S;
int a[maxn];
int bel[maxn], size[maxn], sum[maxn], L[maxn], R[maxn];
int tag[maxn];

void Init() { //分块初始化
	S = sqrt(n);
	for (register int i = 1; i <= n; i ++) {
		bel[i] = (i - 1) / S + 1; //向上取整
		size[bel[i]] ++; //统计每个块的大小，为什么不直接L[i] - R[i]，因为可能最后一个块的大小不是S
		sum[bel[i]] += a[i]; //统计每个块的权值总和
		if (!L[bel[i]]) L[bel[i]] = i; //每个块的左端点
		R[bel[i]] = i; //每个块的右端点
	}
}

void Modify(int l, int r, int w) { //区间修改
	if (bel[l] == bel[r]) { //如果这个区间在同一个块里
		sum[bel[l]] += (r - l + 1) * w; //块的值加上
		for (register int i = l; i <= r; i ++) { //每个单点的值也加上
			a[i] += w;
		}
	}else {
		Modify (l, R[bel[l]], w); //最左边无法组成一个块的
		Modify (L[bel[r]], r, w); //最右边无法组成一个块的
		for (register int i = bel[l] + 1; i < bel[r]; i ++) { //把中间的块加上，并打上花火 &!@*^$&*^*&^@
			tag[i] += w;
			sum[i] += size[i] * w;
		}
	}
}

inline int Query(int l, int r) { //区间查询
	int ans = 0;
	if (bel[l] == bel[r]) {
		ans += (r - l + 1) * tag[bel[l]]; //把之前整块修改的值加上
		for (register int i = l; i <= r; i ++) { // 把之前单点修改后的值加上
			ans += a[i];
		}
	}else {
		ans += Query(l, R[bel[l]]); //最左边无法组成块的值加上
		ans += Query(L[bel[r]], r); //最右边无法组成块的值加上
		for (register int i = bel[l] + 1; i < bel[r]; i ++) {
			ans += sum[i]; //这样我们的sum数组就可以直接查了
		}
	}
	return ans;
}

int main(){
	n = read(), m = read();
	for (register int i = 1; i <= n; i ++) {
		a[i] = read();
	}
	Init();
	while (m --) {
		int opt = read(), l = read(), r = read();
		if (opt == 1) {
			int w = read();
			Modify(l, r, w);
		}else {
			printf("%d
", Query(l, r));
		}
	}
	return 0;
}