逛公园
题目描述
策策同学特别喜欢逛公园。公园可以看成一张 (N) 个点 (M) 条边构成的有向图,且没有自环和重边。其中 (1) 号点是公园的入口,(N) 号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从 (1) 号点进去,从 (N) 号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果 (1) 号点 到 (N) 号点的最短路长为 (d),那么策策只会喜欢长度不超过 (d+K) 的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对 (P) 取模。
如果有无穷多条合法的路线,请输出 (−1) 。
输入格式
第一行包含一个整数 (T), 代表数据组数。
接下来 (T) 组数据,对于每组数据: 第一行包含四个整数 (N,M,K,P),每两个整数之间用一个空格隔开。
接下来 (M) 行,每行三个整数 (a_i,b_i,c_i),代表编号为 (a_i,b_i) 的点之间有一条权值为 (c_i) 的有向边,每两个整数之间用一个空格隔开。
输出格式
输出文件包含 (T) 行,每行一个整数代表答案。
输入输出样例
输入 #1
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0
输出 #1
3
-1
说明/提示
【样例解释1】
对于第一组数据,最短路为 (3)。 (1-5,1-2-4-5,1-2-3-5) 为 (3) 条合法路径。
【测试数据与约定】
对于不同的测试点,我们约定各种参数的规模不会超过如下
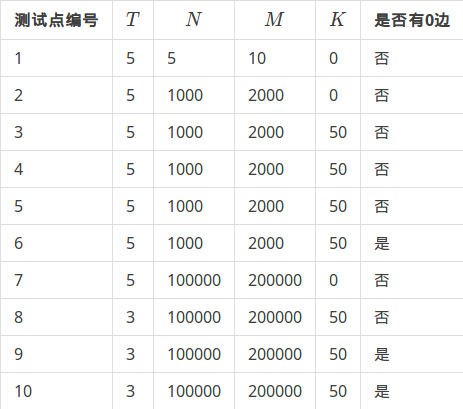
对于 (100\%) 的数据, (1 le P le 10^9,1 le a_i,b_i le N ,0 le c_i le 1000)。
数据保证:至少存在一条合法的路线。
思路
刚开始的求最短路不用说,(SPFA) 和 (dijkstra) 都可,不会有人真的以为这道题会卡 (SPFA) 吧,不会吧,不会吧。

有一说一,前者确实慢,但我就是喜欢
先讨论一下 (-1) 的情况,为什么会出现无穷条路径?
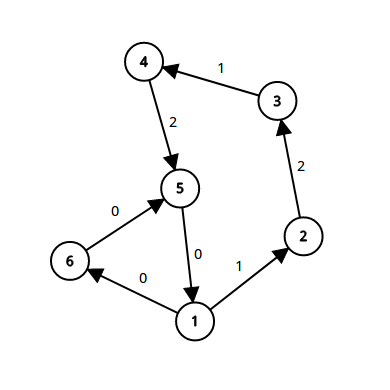
易证,当我们有 (0) 环的时候,我们就会在上图中的 (1-6-5) 这个环里一直走啊走啊走~~~
如果这个环的权值不为 (0),是不是还是 (-1) 呢,显然不是的。
因为在这个环里走的话,你走的路径会越来越长,长度总有一刻会超过限制,所以路径是有限的。
处理完了特殊情况,路径数量怎么求呢?
如果你直接暴搜,恭喜您,您已经取得了 (30opts) 的好成绩,不过,您会 (T) 到飞起。

正解是什么呢?
首先,我们会发现,(k) 的数据范围很小,我们可以从他入手。
直接暴搜???不,我们要有记忆的暴搜。
先建一个反图,反着跑到 (1)。
我们定义一个 (f[i][j]),表示我们跑到了 (i) 点,比最短路 (d) 多 (j) 的长度。
这样我们枚举 (j),疯狂跑,当 (i=1) 并且 (j=0) 时,就是一个答案了。
在判断 (0) 环时,我们就判断一下当前 (f[i][j]) 有没有跑过,如果跑过,直接返回 (-1) 即可。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#define int long long
using namespace std;
const int maxn = 2e5 + 50, INF = 0x3f3f3f3f;
inline int read(){
int x = 0, w = 1;
char ch;
for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
return x * w;
}
int T;
int n, m, k, mod, ans;
struct Edge{
int to, next, w;
}e[maxn], g[maxn];
int tot1, head1[maxn];
void Add1(int u, int v, int w){
e[++tot1].to = v;
e[tot1].w = w;
e[tot1].next = head1[u];
head1[u] = tot1;
}
int tot2, head2[maxn];
void Add2(int u, int v, int w){
g[++tot2].to = v;
g[tot2].w = w;
g[tot2].next = head2[u];
head2[u] = tot2;
}
int dis[maxn];
bool vis[maxn];
void SPFA(int x){//你想跑什么都行,开心就好
memset (dis, 0x3f, sizeof dis);
memset (vis, 0, sizeof vis);
dis[x] = 0;
queue <int> q;
q.push(x);
while (!q.empty()) {
int u = q.front();
q.pop();
vis[u] = 0;
for (register int i = head1[u]; i; i = e[i].next) {
int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
}
}
bool flag[maxn][60];
int dp[maxn][60];
int DFS(int u, int w){
if (w < 0 || w > k) return 0;
if (flag[u][w]) return -1;//跑过这个状态了,返回-1
if (dp[u][w] != -1) return dp[u][w];//如果有记忆化过的,直接返回即可
flag[u][w] = 1;
int sum = 0;
for (register int i = head2[u]; i; i = g[i].next) {
int v = g[i].to;
int tmp = DFS(v, dis[u] + w - dis[v] - g[i].w);//往前跑
if (tmp == -1) return -1;
sum = (sum + tmp) % mod;
}
if (u == 1 && w == 0) {
sum ++;
}
dp[u][w] = sum;
flag[u][w] = 0;
return sum;
}
signed main(){
T = read();
while (T --) {
memset (vis, 0, sizeof vis);//多组数据清空!!!
memset (dp, -1, sizeof dp);//初始为-1,因为有0的情况
memset (flag, 0, sizeof flag);
memset (head1, 0, sizeof head1);
memset (head2, 0, sizeof head2);
memset (e, 0, sizeof e);
ans = 0, tot1 = 0, tot2 = 0;
n = read(), m = read(), k = read(), mod = read();
for (register int i = 1; i <= m; i ++) {
int u = read(), v = read(), w = read();
Add1(u, v, w);
Add2(v, u, w);
}
SPFA(1);
bool pd = 0;
for (register int i = 0; i <= k; i ++) {//枚举k
int now = DFS(n, i);
if (now == -1) {
puts("-1");
pd = 1;
break;
}else {
ans = (ans + now) % mod;
}
}
if (pd == 0) {
printf("%lld
", ans);
}
}
return 0;
}