18.10.9 题目

 bzoj1306 CQOI2009 

这道题就是一个爆搜 然后剪枝很多 很不容易卡过去了

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 10;
int n, a[N], tot = 0, now[N], las[N], ans;
struct mat {
    
    int x, y;
    mat(int x = 0, int y = 0): x(x), y(y) {}
}m[N * N];

void Init( ) {
    
    scanf("%d",& n);
    for(int i = 1;i <= n;i ++) scanf("%d",& a[i]);
    for(int i = 1;i <= n;i ++) {
        for(int j = i + 1;j <= n;j ++) {
            m[++ tot] = mat(i, j);
        }
        las[i] = tot;
    }
}

void dfs(int pos) {
    
    if(pos == tot + 1) {
        for(int i = 1;i <= n;i ++) if(a[i] != now[i]) return ;
        ans ++; return ;
    }
    int u = m[pos].x, v = m[pos].y;
    if(now[u] + 3 * (las[u] - pos + 1) < a[u]) return ;
    if(now[v] + 3 * (las[v] - pos + 1) < a[v]) return ;
    for(int j = 0;j <= 1;j ++) {
        if(j == 1) {
            int t = u; u = v; v = t;
        }
        if(pos == las[u]) {
            if(now[u] + 3 == a[u]) {now[u] += 3; dfs(pos + 1); now[u] -= 3;}
            if(now[u] + 1 == a[u]) {
                now[u] ++; now[v] ++; 
                if(now[v] <= a[v]) dfs(pos + 1);
                now[u] --; now[v] --;
            }
            if(now[u] == a[u]) {now[v] += 3; if(now[v] <= a[v]) dfs(pos + 1); now[v] -= 3;}
            return ;
         }
    }
    u = m[pos].x, v = m[pos].y;
    if(now[u] + 3 <= a[u]) {
        now[u] += 3; dfs(pos + 1); now[u] -=3;
    }
    if(now[u] + 1 <= a[u] && now[v] + 1 <= a[v]) {
        now[u] ++; now[v] ++;
        dfs(pos + 1); now[u] --; now[v] --;
    }
    if(now[v] + 3 <= a[v]) {
        now[v] += 3; dfs(pos + 1); now[v] -= 3;
    }
}

int main( ) {
    
    Init( );
    dfs(1); printf("%d
",ans);
}

JSOI2015 洛谷P4171

一道$2sat$裸题啊 对于昨天才搞过$2sat$的本蒟蒻十分友好了

将每个食材拆成两个点 一个表示做汉菜 一个是满菜 根据约束条件$(i, j)$

连边$(-i, j),(-j, i)$ 然后$tarjan$跑一边强连通分量即可

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2 * 1e3 + 5;
int tot, idc, head[N], nex[2 * N], tov[2 * N], dfn[N], low[N];
int n, m, stk[N], top, cnt, col[N], T;
bool vis[N];
char s1[20], s2[20];

void add(int u, int v) {
    
    tot ++;
    nex[tot] = head[u];
    tov[tot] = v;
    head[u] = tot;
}

void Add_Edge( ) {
    
    memset(col, 0, sizeof(col));
    memset(head, 0 , sizeof(head)); tot = 0;
    memset(dfn, 0, sizeof(dfn)); idc = 0;
    scanf("%d%d",& n,& m); top = 0; cnt = 0;
    for(int i = 1;i <= m;i ++) {
        scanf("%s %s", s1, s2);
        int n1 = s1[0] == 'h' ? 0 : 1;
        int n2 = s2[0] == 'h' ? 0 : 1;
        int u = 0, v = 0, k = 1;
        while(s1[k] >= '0' && s1[k] <= '9') u = u * 10 + s1[k ++] - '0'; k = 1;
        while(s2[k] >= '0' && s2[k] <= '9') v = v * 10 + s2[k ++] - '0';
        if(n1 == 0 && n2 == 0) {add(u + n, v); add(v + n, u);}
        if(n1 == 0 && n2 == 1) {add(u + n, v + n); add(v, u);}
        if(n1 == 1 && n2 == 1) {add(u, v + n); add(v, u + n);}
        if(n1 == 1 && n2 == 0) {add(u, v); add(v + n, u + n);}
    }
}

void tarjan(int u) {
    
    dfn[u] = low[u] = ++ idc;
    vis[u] = true; stk[++ top] = u;
    for(int i = head[u];i;i = nex[i]) {
        int v = tov[i];
        if(! dfn[v]) {
            tarjan(v); low[u] = min(low[u], low[v]);
        }
        else if(vis[v]) low[u] = min(low[u], dfn[v]);
    }
    if(low[u] == dfn[u]) {
        cnt ++;
        while(1) {
            int x = stk[top --];
            vis[x] = false;
            col[x] = cnt;
            if(x == u) break;
        }
    }
}

void Solve( ) {
    
    scanf("%d",& T);
    while(T --) {
        Add_Edge( );
        for(int i = 1;i <= n;i ++) {
            if(! dfn[i]) tarjan(i);
        }
        bool tag = false;
        for(int i = 1;i <= n;i ++) {
            if(col[i] == col[i + n]) tag = true;
        }
        if(tag) printf("BAD
");
        else printf("GOOD
");
    }
}

int main( ) {
    
    Solve( );
}

NOI2015 洛谷P2146

又是一道裸题 线段树套树剖 将已安装的视为$1$ 未安装为$0$

安装则统计从该点到根节点的$0$个数 卸载则统计子树$1$的个数 相应修改即可

代码

#include <bits/stdc++.h>
#define il inline
#define rg register
using namespace std;

const int N = 1e5 + 5;
int n, tot, head[N], nex[2 * N], tov[2 * N], fa[N], size[N];
int tag[4 * N], f[4 * N], top[N], dep[N], in[N], out[N];
int son[N], idc, q;

il int read( ) {
    
    int t = 1, ans = 0;
    char x; x = getchar( );
    while(x < '0' || x > '9') {
        if(x == '-') t = -1;
        x = getchar( );
    }
    while(x >= '0' && x <= '9') {
        ans = ans * 10 + x - '0';
        x = getchar( );
    }
    return ans * t;
}

il void add(int u, int v) {
    
    tot ++;
    nex[tot] = head[u];
    tov[tot] = v;
    head[u] = tot;
}

il void Add_Edge( ) {
    
    n = read( ); int v;
    for(rg int i = 1;i < n;i ++) {
        v = read( );
        add(i + 1, v + 1); add(v + 1, i + 1);
    }
}

il void push_down(int o, int l, int r) {
    
    int mid = l + r >> 1;
    if(tag[o] != -1) {
        tag[2 * o] = tag[o]; tag[2 * o + 1] = tag[o];
        f[2 * o] = tag[o] * (mid - l + 1);
        f[2 * o + 1] = tag[o] * (r - mid);
        tag[o] = -1;
    }
}

il void update(int o) {
    
    f[o] = f[2 * o] + f[2 * o + 1];
}

il int query(int o, int l, int r, int L, int R) {
    
    if(l >= L && r <= R) return f[o];
    push_down(o, l, r);
    int mid = l + r >> 1;
    int num = 0;
    if(L <= mid) num += query(2 * o, l, mid, L, R);
    if(mid < R) num += query(2 * o + 1, mid + 1, r, L, R);
    update(o);
    return num; 
}

il void modify(int o, int l, int r, int L, int R, int del) {
    
    if(l >= L && r <= R) {
        f[o] = del * (r - l + 1);
        tag[o] = del; return ;
    }
    push_down(o, l, r);
    int mid = l + r >> 1;
    if(L <= mid) modify(2 * o, l, mid, L, R, del);
    if(mid < R) modify(2 * o + 1, mid + 1, r, L, R, del);
    update(o);
}

il int Query(int u, int v) {
    
    int num = 0;
    while(top[u] != top[v]) {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        num += query(1, 1, n, in[top[u]], in[u]);
        modify(1, 1, n, in[top[u]], in[u], 1);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    num += query(1, 1, n, in[v], in[u]);
    modify(1, 1, n, in[v], in[u], 1);
    return num;
}

il void dfs1(int u, int fat) {
    
    size[u] = 1; fa[u] = fat;
    for(rg int i = head[u];i;i = nex[i]) {
        int v = tov[i];
        if(v == fat) continue;
        dep[v] = dep[u] + 1;
        dfs1(v, u);
        size[u] += size[v];
        if(size[v] > size[son[u]]) son[u] = v;
    }
}

il void dfs2(int u, int tp) {
    
    top[u] = tp;
    in[u] = ++ idc; 
    if(son[u]) dfs2(son[u], tp);
    for(rg int i = head[u];i;i = nex[i]) {
        int v = tov[i];
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }
    out[u] = idc;
}

il void Solve( ) {
    
    scanf("%d",& q);
    dep[1] = 1; dfs1(1, 1); dfs2(1, 1);
    memset(tag, -1, sizeof(tag));
    for(rg int i = 1;i <= q;i ++) {
        char s[10]; int x;
        scanf("%s",s);
        if(s[0] == 'i') {
            scanf("%d",& x);x ++;
            int num = Query(x, 1);
            num = dep[x] - num;
            printf("%d
",num);
        }
        else {
            scanf("%d",& x);x ++;
            int num = query(1, 1, n, in[x], out[x]);
            modify(1, 1, n, in[x], out[x], 0);
            printf("%d
",num);
        }
    }
}

int main( ) {
    
    Add_Edge( );
    Solve( );
}

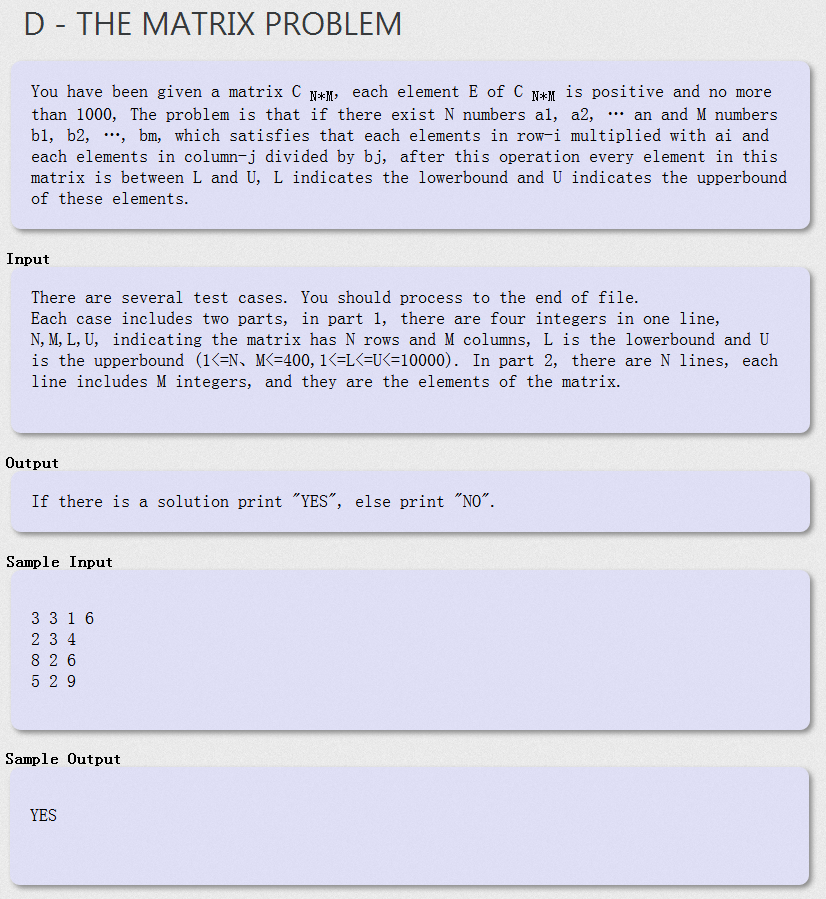
题目大意:

　　给定一个矩阵P 两整数L,R  问是否存在数列a[N]与b[N] 使得L ≤ p[ i ][ j ] * a[ i ] / b[ j ] ≤ R。

这道题是一道差分约束系统的题目 也就是说将一堆不等式化为图论 通过求最短/最长路求解 

对于两不等式 $a - b <= c , b - d <= e$ 建边$(b, a, c),(d, b, e)$ 通过求$b, d$间最短路得到边界条件

将式子化简得到

　　　　　　$L * b[j] <= p[i][j] * a[i] <= R * b[j]$ 

因为两边分别有未知数 所以两边同时取对数化为加减

　　　　      $b[j] - a[i] <= logP[i][j] - logL$

　　　　　  $a[i] - b[j] <= logR - logP[i][j]$

像上述建边 然后跑最短路即可 判断有无解就是判断有无负环 因为一个负环所代表的式子相当于$0 <= x, x$是一个负数 显然不合法叻

普遍的做法是建一个超级源点向每个点连一条边权为$0$的边  无数解的情况则是求解的两个点不连通

但是由于这道题每个点都是互相连通的 所以直接跑也可以

代码

#include <bits/stdc++.h>
#define oo 1e9
using namespace std;

const int N = 400100;
int head[805], nex[N], tov[N], n, m, l, r;
int tot = 0, cnt[N], src;
double val[N], dis[N], p[805][805];
bool tag, vis[N];
queue<int>Q;

void Init( ) {
    
    memset(head, 0, sizeof(head)); tot = 0;
    memset(cnt, 0, sizeof(cnt));   tag = false;
    for(int i = 1;i <= n;i ++) 
        for(int j = 1;j <= m;j ++) scanf("%lf",& p[i][j]);
}

void add(int u, int v, double w) {
    
    tot ++;
    nex[tot] = head[u];
    tov[tot] = v;
    val[tot] = w;
    head[u] = tot;
}

void Add_Edge( ) {
    
    double L = log2(l), R = log2(r);
    for(int i = 1;i <= n;i ++) {
        for(int j = 1;j <= m;j ++) {
            double P = log2(p[i][j]);
            add(i, j + n, P - L);
            add(j + n, i, R - P);
        }
    }
    src = n + m + 1;
    for(int i = 1;i <= n + m;i ++) add(src, i, 0);
}

void spfa( ) {
    
    for(int i = 1;i <= src;i ++) dis[i] = oo;
    memset(vis, 0, sizeof(vis));
    dis[src] = 0; Q.push(src); vis[src] = true;
    while(! Q.empty( )) {
        int u = Q.front( ); Q.pop( ); vis[u] = false;
        for(int i = head[u];i;i = nex[i]) {
            int v = tov[i];
            if(dis[v] - dis[u] - val[i] > 1e-10) {
                dis[v] = dis[u] + val[i];
                if(! vis[v]) {
                    cnt[v] ++;
                    if(cnt[v] > 15) {
                        tag = true; return;
                    }
                    vis[v] = true; Q.push(v);
                }
            }
        }
    }
}

int main( ) {
    
    while(scanf("%d%d%d%d",& n,& m,& l,& r) == 4) {
        Init( );
        Add_Edge( );
        spfa( );
        if(tag) printf("NO
");
        else printf("YES
");
    }
}

SDOI2015 洛谷2483

这道题用$A*$水过去了..滑稽

估价函数写一下 优先队列写一下 $SPFA$写一下 美滋滋

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 5005;
double g[N], e;
int n, m, cnt[N], ans;
bool vis[N];

struct node {
    
    int x; double h;
    node(int x = 0, double h = 0): x(x),h(h) {}
    bool operator < (const node & a) const {
        return h + g[x] > a.h + g[a.x];
    }
};
priority_queue<node>Q;
vector<node>G[N],G1[N];
queue<int>q;

void Init( ) {
    
    scanf("%d%d%lf",& n,& m,& e);
    for(int i = 1;i <= m;i ++) {
        int u, v; double w;
        scanf("%d%d%lf",& u,& v,& w);
        G[u].push_back(node(v, w));
        G1[v].push_back(node(u, w));
    }
}

void spfa( ) {
    
    for(int i = 1;i <= n;i ++) g[i] = 1000000000;
    memset(vis, 0, sizeof(vis));
    q.push(n); g[n] = 0; vis[n] = true;
    while(! q.empty( )) {
        int u = q.front( ); q.pop( ); vis[u] = false;
        for(int i = 0;i < G1[u].size( );i ++) {
            int v = G1[u][i].x;
            if(g[v] > g[u] + G1[u][i].h) {
                g[v] = g[u] + G1[u][i].h;
                if(! vis[v]) {
                    q.push(v); vis[v] = true;
                }
            }
        }
    }
}

void A_star( ) {
    
    double k = e / g[1];
    Q.push(node(1, 0)); 
    while(! Q.empty( )) {
        node u = Q.top( ); Q.pop( );
        int x = u.x; double h = u.h;
        if(h > e) return ;
        cnt[x] ++;
        if(cnt[x] > k) continue;
        if(x == n) {
            ans ++; e -= h; continue;
        }
        for(int i = 0;i < G[x].size( );i ++) {
            int v = G[x][i].x;
            Q.push(node(v, h + G[x][i].h));
        }
    }
}

int main( ) {
    
    Init( ); 
    spfa( );
    A_star( ); 
    printf("%d
",ans);
}