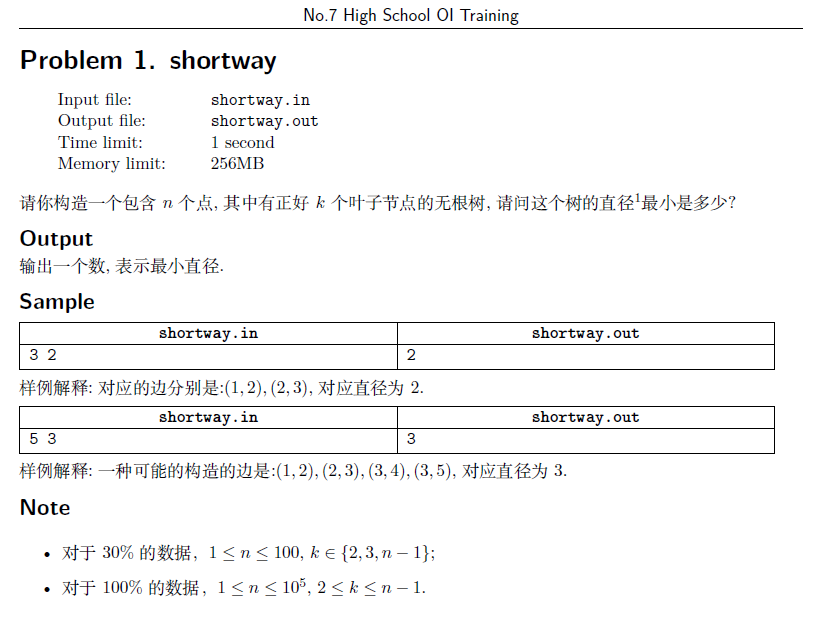
这道题有dalao直接O(1)搞得 然而本蒟蒻只会二分 + 贪心
这道题要使能够容纳的点最多 其实就是一张菊花图
二分枚举直径长度 判断一下能够容纳的点数是否大于等于剩余的点数
点数不够的话我们总可以通过调节链的长度总可以使他合法 就完了
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; int n,k; bool check(int len) { int del = (len - 1) / 2; if((ll)(n - len) <= 1LL * del * (k - 2)) return true; return false; } void solve( ) { int l = 1,r = n,ans = n; while(l <= r) { int mid = (l + r) >> 1; if(check(mid)) ans = mid,r = mid - 1; else l = mid + 1; } printf("%d",ans - 1); } int main( ) { freopen("shortway.in","r",stdin); freopen("shortway.out","w",stdout); scanf("%d%d",& n,& k); solve( ); }

这道题就是一道树状数组的题 我考试的时候调了两个小时 就少了一句话 我恨
因为可以发现e的范围很小 并且每一个小字符串都是一个个怼在上面的
然后可以发现 对于每一个字符串的相同位置 它们模上小字符串的长度的余数都是相等的
所以可以通过状态合并 sum[ i ][ j ][ k ][ id ]表示到了第 i 个位置 模上 j 余数为k的位置 id号字符的个数
所以这个东西就可以通过树状数组维护
代码
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 2; int sum[N][10][10][4],q,LL; char s[N],ss[20]; int find_id(char c) { if(c == 'A') return 0; else if(c == 'G') return 1; else if(c == 'C') return 2; else return 3; } int lowbit(int a) { return a & (-a); } void modify(int pos,int m,int y,int id,int del) { while(pos <= LL) { sum[pos][m][y][id] += del; pos += lowbit(pos); } } void init( ) { LL = strlen(s + 1); for(int m = 1;m <= 10;m ++) for(int i = 1;i <= LL;i ++) { int y = i % m; int id = find_id(s[i]); modify(i,m,y,id,1); } } int query(int pos,int m,int y,int id) { int ans = 0; while(pos >= 1) { ans += sum[pos][m][y][id]; pos -= lowbit(pos); } return ans; } void solve(int l,int r,int len) { int ans = 0; for(int i = 1;i <= len;i ++) { int id = find_id(ss[i]); int st = (l + i - 1) % len; int num = query(r,len,st,id) - query(l - 1,len,st,id); ans += num; } printf("%d ",ans); } void modify(int pos,char c) { int id_las = find_id(s[pos]),id_now = find_id(c); for(int m = 1;m <= 10;m ++) { int y = pos % m; modify(pos,m,y,id_las,-1); modify(pos,m,y,id_now, 1); } s[pos] = c; } int main( ) { freopen("evolution.in","r",stdin); freopen("evolution.out","w",stdout); scanf("%s",s + 1); init( ); scanf("%d",& q); while(q --) { int opt; scanf("%d",& opt); if(opt == 2) { int l,r; scanf("%d%d",& l,& r); scanf("%s",ss + 1); int ll = strlen(ss + 1); solve(l,r,ll); } else { int pos; scanf("%d",& pos); scanf("%s",ss); modify(pos,ss[0]); } } }

对于e( u , v )这条边而言 要使该边一定出现在最小生成树中
这条边的边权就一定要小于所有能够除了该边之外连通u v两个点的链上的最大值的最小的那个
也就是小于u v两个点在最小生成树上的路径中的最大值
所以这条边可能会出现两种情况
1.非树边

根据最小生成树的性质可以知道 对于虚线 它的答案就是浅灰色边中的最大值 - 1
2.树边

对于红色这条边 要使他出现在最小生成树中 那么他一定是连接两个连通块中所有边的最小值
也就是说它小于所有黄色边 那么怎么实现这个东西呢
每次遇到黄色边 就将它的两个端点在树上的路径权值分别与它的值取min(初值赋正无穷)
(因为连接这两个连通块的边在树上的路径一定经过红边) 所以就达到了取min的效果
算法就是mst... 这道题真的代码量好大 改了半天cnm
代码
#include <bits/stdc++.h> #define oo 1e9 using namespace std; const int N = 1e6 + 5; int n,fa[N],fat[N],tot,nex[2 * N],tov[2 * N],ntot,nex1[2 * N]; int head1[N],val[2 * N],val1[2 * N],tov1[2 * N],head[N],co[2 * N]; int m,size[N],son[N],in[N],out[N],seq[N],dep[N],top[N],idc,f[2 * N]; int f1[4 * N],tag[4 * N],ans[N]; bool isnot[N]; struct edge { int u,v,w,id; }e[N]; bool cmp(const edge & a,const edge & b) { return a.w < b.w; } int find_fa(int u) { if(u == fa[u]) return u; return fa[u] = find_fa(fa[u]); } void init( ) { for(int i = 1;i <= n;i ++) fa[i] = i; } void add(int u,int v,int w) { tot ++; nex[tot] = head[u]; tov[tot] = v; head[u] = tot; co[tot] = w; } void add1(int u,int v) { ntot ++; nex1[ntot] = head1[u]; tov1[ntot] = v; val1[ntot] = oo; head1[u] = tot; } void build( ) { for(int i = 1;i <= m;i ++) { int u = e[i].u,v = e[i].v; int fa1 = find_fa(u),fa2 = find_fa(v); if(fa1 == fa2) { isnot[e[i].id] = true; continue; } else { fa[fa2] = fa1; add(u,v,e[i].w); add(v,u,e[i].w); } } } void dfs1(int u,int fa) { size[u] = 1; fat[u] = fa; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v == fa) continue; dep[v] = dep[u] + 1; dfs1(v,u); val[v] = co[i]; size[u] += size[v]; if(size[v] > size[son[u]]) son[u] = v; } } void dfs2(int u,int tp) { top[u] = tp; idc ++; in[u] = idc; seq[idc] = u; if(son[u]) dfs2(son[u],tp); for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v == fat[u] || v == son[u]) continue; dfs2(v,v); } } void update(int o) { f[o] = max(f[2 * o],f[2 * o + 1]); } void build_tree1(int o,int l,int r) { if(l == r) { f[o] = val[seq[l]]; return ; } int mid = (l + r) >> 1; build_tree1(2 * o,l,mid); build_tree1(2 * o + 1,mid + 1,r); update(o); } int query_tree(int o,int l,int r,int L,int R) { if(l >= L && r <= R) { return f[o]; } int mid = (l + r) >> 1; int ans = 0; if(L <= mid) ans = query_tree(2 * o,l,mid,L,R); if(mid < R) ans = max(ans,query_tree(2 * o + 1,mid + 1,r,L,R)); return ans; } int query(int u,int v) { int ans = 0; while(top[u] != top[v]) { if(dep[top[u]] < dep[top[v]]) swap(u,v); int cmp = query_tree(1,1,idc,in[top[u]],in[u]); ans = max(ans,cmp); u = fat[top[u]]; } if(dep[u] < dep[v]) swap(u,v); ans = max(ans,query_tree(1,1,idc,in[v] + 1,in[u])); return ans; } void push_down(int o) { if(tag[o]) { if(tag[2 * o]==0) tag[2 * o] = tag[o]; else tag[2 * o] = min (tag[2 * o],tag[o]); if(tag[2 * o + 1]==0) tag[2 * o + 1] = tag[o]; else tag[2 * o + 1] = min (tag[2 * o + 1],tag[o]); f1[2 * o] = min(f1[2 * o],tag[o]); f1[2 * o + 1] = min(f1[2 * o + 1],tag[o]); tag[o] = 0; } } void modify(int o,int l,int r,int L,int R,int w) { if(l >= L && r <= R) { f1[o] = min(f1[o],w - 1); if(tag[o]==0) tag[o] = w - 1; else tag[o] = min(w - 1,tag[o]); return ; } push_down(o); int mid = (l + r) >> 1; if(L <= mid) modify(2 * o,l,mid,L,R,w); if(mid < R) modify(2 * o + 1,mid + 1,r,L,R,w); } void modify_tr2(int u,int v,int w) { while(top[u] != top[v]) { if(dep[top[u]] < dep[top[v]]) swap(u,v); modify(1,1,idc,in[top[u]],in[u],w); u = fat[top[u]]; } if(dep[u] < dep[v]) swap(u,v); modify(1,1,idc,in[v] + 1,in[u],w); } int query_tr2(int o,int l,int r,int pos) { if(l == r) { return f1[o]; } push_down(o); int mid = (l + r) >> 1; if(pos <= mid) return query_tr2(2 * o,l,mid,pos); else return query_tr2(2 * o + 1,mid + 1,r,pos); } int main( ) { freopen("mst.in","r",stdin); freopen("mst.out","w",stdout); scanf("%d%d",& n,& m); init( ); for(int i = 1;i <= m;i ++) { int u,v,w; scanf("%d%d%d",& u,& v,& w); e[i].u = u; e[i].v = v; e[i].w = w; e[i].id = i; } memset(tag,0x3f3f3f,sizeof(tag)); memset(f1,0x3f3f3f,sizeof(f1)); int p = f1[0]; dep[1] = 1; sort(e + 1,e + m + 1,cmp); build( ); dfs1(1,1); dfs2(1,1); build_tree1(1,1,idc); for(int i = 1;i <= m;i ++) { int fu = e[i].id; if(isnot[fu]) { ans[fu] = query(e[i].u,e[i].v) - 1; modify_tr2(e[i].u,e[i].v,e[i].w); } } for(int i = 1;i <= m;i ++) { int fu = e[i].id; if(! isnot[fu]) { int u = dep[e[i].u] > dep[e[i].v] ? e[i].u : e[i].v; ans[fu] = query_tr2(1,1,idc,in[u]); if(ans[fu] == p) ans[fu] = -1; } } for(int i = 1;i <= m;i ++) printf("%d ",ans[i]); }