
这道题我考场上面是打表找规律...然后就找出来了嘛...
就递推打打表就好了
然后正解的想法是贪心取4 然后剩下的余数用来配和数
代码
#include <bits/stdc++.h> using namespace std; int q,ans[20] = {-1,-1,-1,-1,1,-1,1,-1,2,1,2,-1}; int n; int main( ) { freopen("split.in","r",stdin); freopen("split.out","w",stdout); scanf("%d",& q); while(q --) { scanf("%d",& n); if(n <= 11) printf("%d ",ans[n]); else { int a = n / 4; int b = n % 4; if(b == 1 || b == 3) printf("%d ",a - 1); else printf("%d ",a); } } }
附一个我打表找规律的代码吧..
#include <bits/stdc++.h> using namespace std; const int N = 1e4 + 10; bool vis[N]; int num[N],q; void init( ) { for(int i = 1;i <= 10000;i ++) { int j; for(j = 2;j * j <= i;j ++) { if(i % j == 0) break; } if(j * j > i) vis[i] = true; } } int main( ) { init( ); for(int i = 1;i <= 1e4;i ++) { if(vis[i]) num[i] = -1; else num[i] = 1; for(int j = 1;j <= i / 2;j ++) { if(num[j] == -1 || num[i - j] == -1) continue; num[i] = max(num[j] + num[i - j],num[i]); } } scanf("%d",& q); while(q --) { int x; scanf("%d",& x); printf("%d ",num[x]); } }

这道题又是一道并查集...又是一道yyyuuu大佬在考场上面就切掉的神题...
并查集就把 x 和 y 相同的所有点并到一起 就像这样
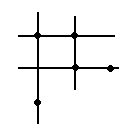
然后对于不同的并查集的点 他们的贡献是互不影响的 就可以直接乘起来
那么现在问题就变成了怎么求一个并查集能够产生的贡献 考试的时候想不到 后面idy讲的时候给我们介绍了一种清奇的做法
将点看做边 边看做点 那么对于一个点( a , b ) 就将 a 向 b 连边 表示这个点既可以发出 x = a 也可以发出y = b 的直线
因为是[ -1e9 , 1e9 ]的范围 所以需要预先对所有 x y 离散化
因为每个点只能管辖一条线 所以就考虑并查集并起来之后每个连通块的情况
因为它是一个连通块 所以他至少是一棵树 其次就是有环连通图
所以我们就对连通块的情况进行讨论
1.树
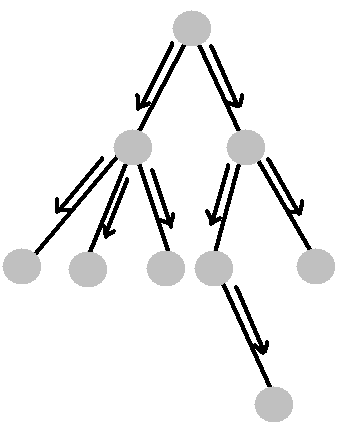
以这个图为例 箭头表示该条边所代表的点去管辖哪一条边
如果我不选最上面的那个点 也就是我不选择它所对应的直线 那么就可以沿边向下扩展
表示这条边所对应的点去管辖另外一条边了 所以这样子拓展剩下的每个点所代表的边都会被一个点所管辖到
那么也就是说除了第一个点 剩下的点所代表的边的子集都是可以取到的 因为每个点也可以选择不去管辖边
方案数就是2点数 - 1 也就是2S|x| + S|y| - 1
2.带环连通图
因为它带环 所以每个点所代表的边就都可以被管辖到
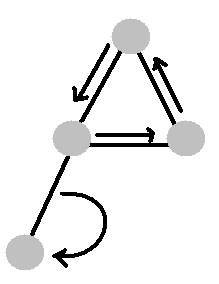
也就是说所有直线及他们的子集都可以取到 那么方案数就是2点数也就是2S|x| + S|y|
最后把每个连通块的方案乘起来就可以了
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 4 * 1e5 + 5; const ll mod = 1e9 + 7; int n,tot,head[N],tov[N],nex[N],fa[N],size[N]; int x[N],y[N],my,mx,xxx[N],yyy[N]; ll poww[N],ans = 1; bool tag = false,vis[2 * N],vv[2 * N]; void add(int u,int v) { tot ++; nex[tot] = head[u]; tov[tot] = v; head[u] = tot; } void dfs(int u,int fa) { vis[u] = true; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v == fa) continue; if(vis[v]) { tag = true; return ;} dfs(v,u); } return ; } int find_fa(int u) { return u == fa[u] ? u : fa[u] = find_fa(fa[u]); } void init( ) { for(int i = 1;i <= 2 * n;i ++) fa[i] = i,size[i] = 1; sort(x + 1,x + n + 1); mx = unique(x + 1,x + n + 1) - x - 1; sort(y + 1,y + n + 1); my = unique(y + 1,y + n + 1) - y - 1; poww[0] = 1; for(int i = 1;i < N;i ++) poww[i] = poww[i - 1] * 2 % mod; } int main( ) { freopen("cross.in","r",stdin); freopen("cross.out","w",stdout); scanf("%d",& n); for(int i = 1;i <= n;i ++) { scanf("%d%d",& x[i],& y[i]); xxx[i] = x[i],yyy[i] = y[i]; } init( ); for(int i = 1;i <= n;i ++) { int X = xxx[i],Y = yyy[i]; int u = lower_bound(x + 1,x + mx + 1,X) - x; int v = lower_bound(y + 1,y + my + 1,Y) - y + mx; add(u,v); add(v,u); int xx = find_fa(u),yy = find_fa(v); if(xx != yy) { size[xx] += size[yy]; fa[yy] = xx; } } ll ans = 1; for(int i = 1;i <= n;i ++) { int siz; int xx = lower_bound(x + 1,x + mx + 1,x[i]) - x; int fat = find_fa(xx); tag = false; if(! vv[fat]) { vv[fat] = true; dfs(xx,xx); siz = size[fat]; if(tag) ans = ans * poww[siz] % mod; else ans = ans * (poww[siz] - 1) % mod; } } printf("%I64d",ans); }

这道题是非常暴力的...看到这个100 的数据范围 就觉得应该是乱搞...
对于一个长度为k的串 我们可以得出一个不等式
$100cdot(100 - k + 1) + 100cdot kgeq 2^{k}$
100 - k + 1表示一开始没进行合并时总共每个串内最多可出现所少个不同的长度为k的串
*100就表示一开始总共有多少个 每次合并最多产生近似k个不同的串

因为只有跨越ab交接点的串是新产生的 这种串的起点最多是交接点 - k的位置 ~ 交接点 大约为k个
所以总共的长度为k的串的个数要≥2k才合法 解出来可以发现k的范围是非常小的 大约是11 12 的样子
所以就更愿意乱搞了...!! 首先对于所有长度从1 - 12 递增的不同的串编号
定义f[ i ][ j ]表示第 i 号串有没有编号为 j 的字串
假设a串 b串合成x串 那么f[ x ][ j ] |= f[ a ][ j ] |= f[ b ][ j ] 这是转移已有的信息
然后再乱搞搞把中间新的字串搞出来就可以了 非常naive
因为我们每次乱搞都只搞中间的部分 所以我们只需要保留一个串的前12位和后12位就可以了
总之这道题就是乱搞搞
代码(还是叫idy帮忙看的 细节太难了我真的调不出来 敲你m)
#include <bits/stdc++.h> using namespace std; const int N = 1e3 + 5; const int M = (1 << 13); string s[N]; int n,id[N][M],tot = 0,len[300],st[N],ed[N],l[N][M],m; bool f[N][M]; void init( ) { for(int i = 1;i <= 12;i ++) { for(int j = 0;j < (1 << i);j ++) { id[i][j] = ++ tot; if(j == 0) st[i] = tot; } ed[i] = tot; } } void work(int i) { for(int p = 1;p <= 12;p ++) { if(p > len[i]) break; for(int j = 0;j < len[i];j ++) { if(j + p - 1 >= len[i]) break; int cmp = 0; for(int t = j;t <= j + p - 1;t ++){ cmp <<= 1; cmp |= (s[i][t] - '0'); } f[i][id[p][cmp]] = true; } } } void solve(int x,int a,int b) { string sss = s[a] + s[b]; if(sss.length( ) > 24) { s[x].clear(); for(int i = 0;i <= 11;i ++) s[x].push_back(sss[i]); for(int i = sss.length( ) - 12;i < sss.length( );i ++) s[x].push_back(sss[i]); } else { s[x] = sss; } int ll = s[x].length( ); for(int i = 1;i <= tot;i ++) if(f[a][i] || f[b][i]) f[x][i] = true; for(int l1 = 1; l1 <= 12; l1++) for(int l2 = 1; l2 <= 12; l2++) { if(1 <= l1 + l2 && l1 + l2 <= 12) { int cmp = 0; for(int k = s[a].size() - l1; k < s[a].size(); k++) { cmp <<= 1; cmp |= (s[a][k] - '0'); } for(int k = 0; k < l2; k++) { cmp <<= 1; cmp |= (s[b][k] - '0'); } f[x][id[l1+l2][cmp]] = true; } } /* for(int i = 2;i <= 12;i ++) { for(int j = ll - i + 1;j < ll;j ++) { if(j < 0) continue; int cmp = 0; if(j + i - 1 >= ll) continue; for(int k = j;k <= j + i - 1;k ++) { cmp <<= 1; cmp |= (ss[k] - '0'); } if(! f[x][id[i][cmp]]) f[x][id[i][cmp]] = true; } } */ int i; for(i = 12;i >= 1;i --) { bool tag = false; for(int j = st[i];j <= ed[i];j ++) if(! f[x][j]) { tag = true; break; } if(! tag) { printf("%d ",i); break; } } if(i == 0) printf("0 "); } int main( ) { freopen("string.in","r",stdin); freopen("string.out","w",stdout); scanf("%d",& n); init( ); for(int i = 1;i <= n;i ++) { cin >> s[i]; len[i] = s[i].length( ); work(i); } scanf("%d",& m); for(int i = 1;i <= m;i ++) { int a,b; scanf("%d%d",& a,& b); solve(n + i,a,b); } return 0; }