1019-计算二叉树的高度和结点数

描述

 

二叉树是非常重要的树形数据结构，根据该树的先序、中序或后序遍历序列可以建立一棵二叉树。例如输入先序遍历序列A B # D # # C E # # F # #可以建立图1019-1所示的二叉树，这里用#代表空树或空子树（另一种说法：若无孩子结点，则用#代替），如图1019-2。

 

图1019-1

 

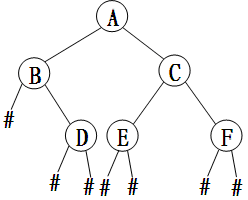
图1019-2

请实现基于遍历的二叉树运算：求高度、计算结点数目

输入

 

二叉树的先序遍历序列，用#代表空树或空子树。

输出

 

共五行

前三行依次输出先序、中序和后序遍历序列，

第四行输出二叉树的高度，

第五行依次输出二叉树总结点数目、叶子结点数目、度为1的结点数目。

样例输入

A B # D # # C E # # F # #

样例输出

PreOrder: A B D C E F

InOrder: B D A E C F

PostOrder: D B E F C A 3 6 3 1

#include <iostream>
using namespace std;
class BTNode
{
public:
    char data;
    BTNode *lChild;
    BTNode *rChild;
};
void Creat(BTNode *&t)
{
    char c;
    cin>>c;
    if(c=='#')
        t=NULL;
    else
    {
        t=new BTNode;
        t->data=c;
        t->lChild=NULL; 
        t->rChild=NULL;
        Creat(t->lChild);
        Creat(t->rChild);
    }
}
void PreOrder(BTNode *&t)
{   
    if(t)
    {
        cout<<" "<<t->data;
        PreOrder(t->lChild);
        PreOrder(t->rChild);
    }
}
void InOrder(BTNode *&t)
{
    if(t)
    {        
        InOrder(t->lChild);
        cout<<" "<<t->data;
        InOrder(t->rChild);
    }
}
void PostOrder(BTNode *&t)
{
    if(t)
    {        
        PostOrder(t->lChild);
        PostOrder(t->rChild);
        cout<<" "<<t->data;
    }
}
int H(BTNode *&t)
{ 
    int lh,rh;
    if(t==NULL)
        return 0;
    else
    {
        lh=H(t->lChild)+1;
        rh=H(t->rChild)+1;
    }
    if(lh>=rh) return lh;
    else return rh;
}
int Sum(BTNode *&t,int &m)
{   
    if(t)
    {
        m++;
        Sum(t->lChild,m);
        Sum(t->rChild,m);
    }
    return m;
}
int L(BTNode *&t,int &leaf)
{   
    if(t)
    {
        if(t->lChild==NULL&&t->rChild==NULL)
            leaf++;
        L(t->lChild,leaf);
        L(t->rChild,leaf);
    }
    return leaf;
}
int M(BTNode *&t,int &m1)
{   
    if(t)
    {
        if((t->lChild&&t->rChild==NULL)||(t->lChild==NULL&&t->rChild))
            m1++;
        M(t->lChild,m1);
        M(t->rChild,m1);
    }
    return m1;
}
int main()
{
    int m=0,leaf=0,m1=0;
    BTNode *t;
    Creat(t);
    cout<<"PreOrder:";
    PreOrder(t);
    cout<<endl;
    cout<<"InOrder:";
    InOrder(t);
    cout<<endl;
    cout<<"PostOrder:";
    PostOrder(t);
    cout<<endl;
    cout<<H(t)<<endl;
    cout<<Sum(t,m)<<" "<<L(t,leaf)<<" "<<M(t,m1)<<endl;
    return 0;
}