如何让孩子爱上打表
Catalan数
Catalan数是组合数学中一个常出现在各种计数问题中的数列。
以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名。
先丢个公式(设第n项为$h_n$):
$h_n=h_0*h_{n-1}+h_1*h_{n-2}+...+h_{n-1}*h_0,(n ge 2)$
$h_n=frac{h_{n-1}*(4n-2)}{n+1}$
$h_n=C_{2n}^n-C_{2n}^{n-1}=frac{C_{2n}^n}{n+1}$
应用
出栈次序是卡特兰数的一个应用。
我们将入栈视为+1,出栈视为-1,则限制条件为在任意位置前缀和不小于0 。
我们讨论这个问题与卡特兰数有什么关系。 为了方便,我们按入栈的先后顺序将各个元素由1到n编号。
假设最后一个出栈的数为k。 则在k入栈之前,比k小的数一定全部出栈,所以这部分方案数为h(k-1)。
在k入栈之后,比k大的数在k入栈之后入栈,在k出栈之前出栈,所以这部分的方案数为h(n-k)。
这两部分互不干扰,则方案数为h(k-1)*h(n-k) 枚举k,得到的公式就是卡特兰数的递推公式。
——WangKoala
大部分Catalan数的题目都可以抽象为这样一个模型,所以深刻理解第一个递推式对快速分析出题目与Catalan有关很有帮助。
(其实还是打表最快hhh)
另外,有的题目则根据Catalan数的组合意义构造模型,比如下面的第一道题。
题目
3907: 网格
Time Limit: 1 Sec Memory Limit: 256 MBSubmit: 1035 Solved: 367
[Submit][Status][Discuss]
Description
.png)
Input
输入文件中仅有一行,包含两个整数n和m,表示城市街区的规模。
Output
输出文件中仅有一个整数和一个换行/回车符,表示不同的方案总数。
Sample Input
Sample Output
HINT
首先考虑n*n的情况。不难发现此时答案即为Catalan数。
如果没有线的限制,从$(0,0)-->(n,n)$的总方案数为$C_{2n}^n$
考虑它的含义:$2n$次操作,其中选$n$次向上走
接下来需要考虑不合法的情况并减去它。
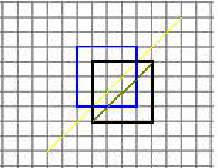
黄线可以看作合法与不合法情况的分界(一碰就不合法)
我们将矩形沿这条线对称过去,那么碰到黄线后走到$(n,n)$的走法 就可以对称为碰到黄线走到$(n-1,n+1)$的走法。
那么显然不合法方案数为$C_{2n}^{n-1}$。($2n$次操作中有$n-1$次向右,你把它写成$C_{2n}^{n+1}$也无所谓 反正它们相等)
至于$n!=m$的情况,以此类推即可。
$ans=C_{n+m}^n-C_{n+m}^{m-1}$
对于组合数计算,分解质因数约分后用高精乘低精统计即可。没必要高精除。

#include<cstdio> #include<iostream> #include<cstring> #include<vector> using namespace std; int n,m; int pri[1600],tot,vis[10005]; int bu[1600],num1[100005],num2[100005],ans[100005]; void getpri() { for(int i=2;i<=10000;i++) { if(!vis[i])pri[++tot]=i; for(int j=1;j<=tot;j++) { if(i*pri[j]>10000)break; vis[i*pri[j]]=1; if(i%pri[j]==0)break; } } } void print(int a[]) { for(int i=a[0];i>=1;i--) printf("%d",a[i]); puts(" "); } void div1(int x) { for(int i=1;pri[i]<=x&&x!=1;i++) while(x%pri[i]==0)x/=pri[i],bu[i]++; } void div2(int x) { for(int i=1;pri[i]<=x&&x!=1;i++) while(x%pri[i]==0)x/=pri[i],bu[i]--; } void mult(int x,int a[]) { int k=0; for(int i=1;i<=a[0];i++) { int tmp=a[i]*x+k; a[i]=tmp%10; k=tmp/10; } while(k)a[++a[0]]=k%10,k/=10; } void Minus(int a[],int b[]) { int j=1,x=0; while(j<=a[0]||j<=b[0]) { if(a[j]<b[j]) { a[j]+=10; a[j+1]--; } ans[j]=a[j]-b[j]; j++; } int k=j; while(ans[k]==0&&k>1)k--; ans[0]=k; } int main() { getpri(); scanf("%d%d",&n,&m); /* div1(n); for(int i=1;i<=10;i++)cout<<bu[i]<<' '; div2(m); for(int i=1;i<=10;i++)cout<<bu[i]<<' ';*/ for(int i=n+m;i>=m+1;i--) div1(i); for(int i=n+1;i>=2;i--) div2(i); num1[0]=num1[1]=1; for(int i=1;i<=1600;i++) { if(!pri[i])break; if(!bu[i])continue; while(bu[i]) mult(pri[i],num1),bu[i]--; } //print(num1); for(int i=0;i<=num1[0];i++) num2[i]=num1[i]; mult(n+1,num1);mult(m,num2); //print(num1);print(num2); Minus(num1,num2); print(ans); return 0; }
1485: [HNOI2009]有趣的数列
Time Limit: 10 Sec Memory Limit: 64 MBSubmit: 2252 Solved: 1205
[Submit][Status][Discuss]
Description
我们称一个长度为2n的数列是有趣的,当且仅当该数列满足以下三个条件:
(1)它是从1到2n共2n个整数的一个排列{ai};
(2)所有的奇数项满足a1<a3<…<a2n-1,所有的偶数项满足a2<a4<…<a2n;
(3)任意相邻的两项a2i-1与a2i(1≤i≤n)满足奇数项小于偶数项,即:a2i-1<a2i。
现在的任务是:对于给定的n,请求出有多少个不同的长度为2n的有趣的数列。因为最后的答案可能很大,所以只要求输出答案 mod P的值。
Input
输入文件只包含用空格隔开的两个整数n和P。输入数据保证,50%的数据满足n≤1000,100%的数据满足n≤1000000且P≤1000000000。
Output
仅含一个整数,表示不同的长度为2n的有趣的数列个数mod P的值。
Sample Input
Sample Output
5
对应的5个有趣的数列分别为(1,2,3,4,5,6),(1,2,3,5,4,6),(1,3,2,4,5,6),(1,3,2,5,4,6),(1,4,2,5,3,6)。
打表找规律可得答案为Catalan数。
这题如果强行想的话会很困难 而且比较浪费时间 所以不如直接打表找规律。
还是分解质因数约分,统计时取模即可。

#include<cstdio> #include<iostream> #include<cstring> using namespace std; typedef long long ll; ll mod,ans=1; int n,pri[150005],tot,vis[2000005]; int bu[150005],maxi=0,res[2000005]; void getprime() { for(int i=2;i<=2*n;i++) { if(!vis[i])pri[++tot]=i,res[i]=tot; for(int j=1;j<=tot;j++) { if(i*pri[j]>2*n)break; vis[i*pri[j]]=1;res[i*pri[j]]=j; if(i%pri[j]==0)break; } } } void divi(int x,int val) { while(x!=1)bu[res[x]]+=val,x/=pri[res[x]]; } int main() { scanf("%d%lld",&n,&mod); getprime(); for(int i=2*n;i>=n+1;i--) divi(i,1); for(int i=n+1;i>=2;i--) divi(i,-1); for(int i=1;i<=tot;i++) while(bu[i]--)ans=1LL*pri[i]*ans%mod; cout<<ans<<endl; return 0; }
2822: [AHOI2012]树屋阶梯
Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 1204 Solved: 716
[Submit][Status][Discuss]
Description
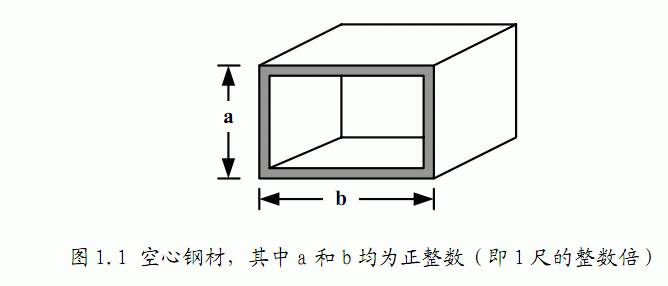
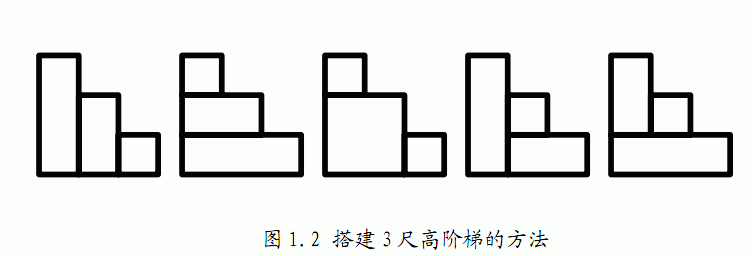
以树屋高度为4尺、阶梯高度N=3尺为例,小龙一共有如图1.2所示的5种
搭 建方法:
Input
一个正整数 N(1≤N≤500),表示阶梯的高度
Output
一个正整数,表示搭建方法的个数。(注:搭建方法个数可能很大。)
Sample Input
Sample Output
HINT
1 ≤N≤500
一个大小为i的阶梯,都可以看作由左上角一块j和右下角一块i-j-1的阶梯,再用矩形填充空缺构成。
这样构成的阶梯算下来正好是用i个钢材,且方案各不相同。
j在0--i-1取值,可得方案数的递推式:
$h_n=h_0*h_{n-1}+h_1*h_{n-2}+...+h_{n-1}*h_0,(n ge 2)$
这显然就是Catalan的递推式。

#include<cstdio> #include<iostream> #include<cstring> using namespace std; int n; int pri[1000005],tot,vis[1000005],res[1000005]; int bu[1000005],ans[50005]; void getpri() { for(int i=2;i<=2*n;i++) { if(!vis[i])pri[++tot]=i,res[i]=tot;; for(int j=1;j<=tot;j++) { if(i*pri[i]>2*n)break; vis[i*pri[j]]=1;res[i*pri[j]]=j; if(i%pri[j]==0)break; } } } void print(int a[]) { for(int i=a[0];i>=1;i--) printf("%d",a[i]); puts(" "); } void divi(int x,int val) { while(x!=1)bu[res[x]]+=val,x/=pri[res[x]]; } void mult(int x,int a[]) { int k=0; for(int i=1;i<=a[0];i++) { int tmp=a[i]*x+k; a[i]=tmp%10; k=tmp/10; } while(k)a[++a[0]]=k%10,k/=10; } int main() { scanf("%d",&n); getpri(); for(int i=2*n;i>=n+1;i--) divi(i,1); for(int i=n+1;i>=1;i--) divi(i,-1); ans[0]=ans[1]=1; for(int i=1;i<=tot;i++) while(bu[i]--)mult(pri[i],ans); print(ans); return 0; }
