CF982 C Cut 'em all!【树/DFS/思维】

【链接】：CF982C
【题意】：有一颗树，你需要切掉一些边，使这颗树分拆成若干个节点为偶数的联通分量，最多能切掉几条边。若不能切,输出-1。

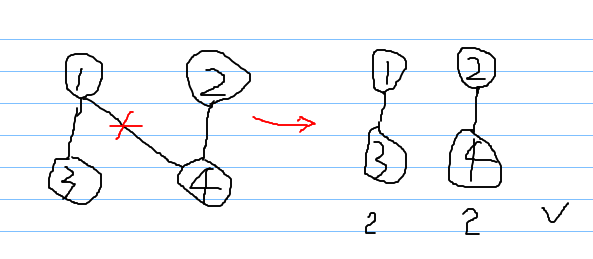
【分析】：
1.若点数n为奇数，因为奇数不可能分为偶数，那么一定输出-1
2.若点数n为偶数，偶数=偶数+偶数。就从顶点1开始，当作父顶点开始dfs。dfs用于计算子树的顶点数，如果子树是偶数个顶点，那么ans就可以++，然后把该子树标记成搜索过的，最后的答案要-1；因为整棵树肯定是偶数顶点，ans也会+1；
【代码】:
[不用vis数组]

#include<bits/stdc++.h>
using namespace std;
typedef long long  ll;
const int maxn = 2*1e5+5;
const ll INF = 2147483647;
typedef pair<ll ,int> pli;
vector<int> G[maxn];
int ans;
int vis[maxn];
int dfs(int x,int fa)
{
    int sum=1; //我们在讨论子数结点数一般是包括根结点自身的
    for(int i=0; i<G[x].size(); i++)
    {
        int u = G[x][i];
        if(u!=fa)
        {
            sum+=dfs(u,x);
        }
    }
    if(sum%2==0) ans++;
    return sum;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    if(n&1)
    {
        puts("-1");
        return 0;
    }
    dfs(1,0);
    cout<<ans-1<<endl;//原本自己就是偶数，所以要减1
}

---

[用vis数组]

#include<bits/stdc++.h>
using namespace std;
typedef long long  ll;
const int maxn = 2*1e5+5;
const ll INF = 2147483647;
typedef pair<ll ,int> pli;
vector<int> G[maxn];
int ans;
int vis[maxn];
int dfs(int x)
{
    int sum=1;
    vis[x]=1;
    for(int i=0; i<G[x].size(); i++)
    {
        int u = G[x][i];
        if(!vis[u])
        {
            sum+=dfs(u);
        }
    }
    if(sum%2==0) ans++;
    return sum;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    if(n&1)
    {
        puts("-1");
        return 0;
    }
    dfs(1);
    cout<<ans-1<<endl;
}