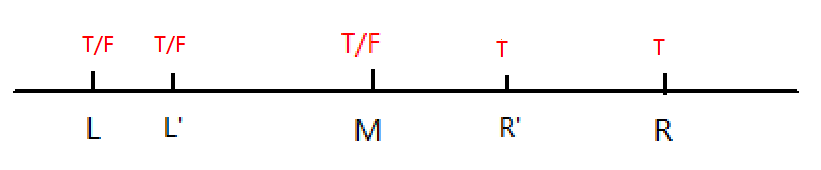
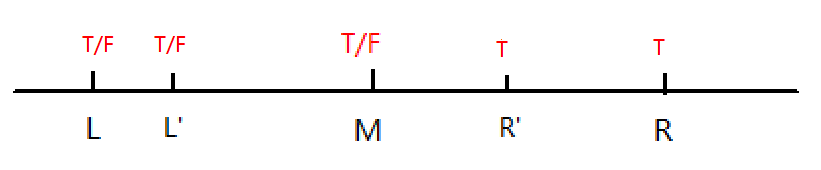
二分
•主要用于在一个单调的函数中查询某值
连续函数的情况:
• 若当前查找的区间是 [l, r] ,查询的值是 y ,函数单增
• 设 mid = (l + r) / 2 若 f(mid) < y 则 l = mid, 否则 r = mid
• 直至 r - l < eps
离散函数的情况:
• 当前查找的区间是 [l, r] ,查询的值是 y ,函数单增
• 设 mid = (l + r) / 2 若 f(mid) = y 则 return mid
• 若 f(mid) < y 则 l = mid + 1, 否则 r = mid - 1
二分法
经常有这样的问题,求xxx最小值的最大值,即求符合条件的值里的最大值,这种问题有个解法叫二分答案法。一听,什么,不知道的答案也能二分?嗯没错,关键在于这个答案是可以判断是不是符合条件的。
算法思想
以求最小值的最大值(最小值最大化)为例,尝试一个可能的答案,如果这个答案符合题目条件,那么它肯定是“最小”(可行解),但不一定是“最大”(最优解),然后我们换个更大的可能答案,如果也符合条件,那这个新可行解就更优,不断重复即可。怎么找呢?这时就该二分上场了。
二分答案的主要思想
• 就是在答案的可能范围(区间)内二分枚举
• 并检查所穷举的答案是否符合题意。
• 可以将最优性问题(直接求解相对较难)
• 转化为可行性问题(答案是否符合题意相对容易)
二分答案的适用范围(条件)
• 二分答案当且仅当答案的范围已知且具有单调性的时候才可以使用。
• 一般也是求最优值问题• 更多、更明显的标志是:
• “最大值最小化” 或者 “最小值最大化”
二分答案的框架• 假设答案是单调递增的,要求的是“最小值”
• l = 答案下限,r = 答案上限
• while (l <= r)
• {
• mid = (l + r) >> 1;
• if check(mid) ans = mid, r = mid - 1; else l = mid + 1;
• }
• return ans;
二分答案的难点(关键)
• 如何检验当前的答案是否符合题目的要求(限制条件)?
• 常见的方法:穷举、贪心、搜索、动态规划、图论、数据结构等
• 可以看到,二分答案问题很好地结合了其他算法知识,非常受命题者欢迎
• NOIP 2010 以来经常出现,例如 NOIP 2015 D1T2 跳⽯头
二分前提
1.答案区间上下限确定,即最终答案在哪个范围是容易知道的。
2.检验某值是否可行是个简单活,即给你个值,你能很容易的判断是不是符合题目要求。
3.可行解满足区间单调性,即若x是可行解,则在答案区间内x+1(也可能是x-1)也可行。
两种情况
1.最小值最大化
int l = min_ans, r = max_ans;
while (l < r) {
int mid = (l + r + 1) / 2; //+1避免 r == l + 1 时mid一直等于l,从而死循环
if (ok(mid)) //符合条件返回True
l = mid;
else
r = mid - 1;
}
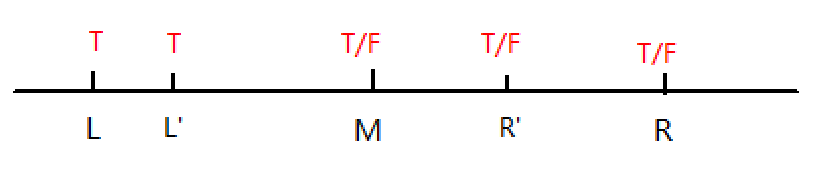
2.最大值最小化
int l = min_ans, r = max_ans;
while (l < r) {
int mid = (l + r) / 2;
if (ok(mid)) //符合条件返回True
r = mid;
else
l = mid + 1;
}
按同样道理分析,维持R的True属性即可。这里的mid就不需要加1了,因为 mid 跟 l 重合时,l = mid + 1;会自增,而当 mid 和 r 重合时 l 也跟 r 重合,结束循环了。
注意点
l = mid; r = mid;
三分法
当二分的函数值不是递增/减,而是先增后减或者先减后增时二分就挂了。此时需要三分法,这里直接盗用hihocoder Problem 1142的图(hihocoder需要注册登陆,没登陆进不去)
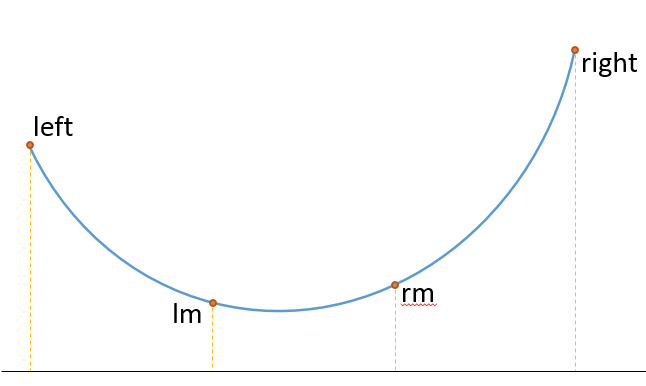
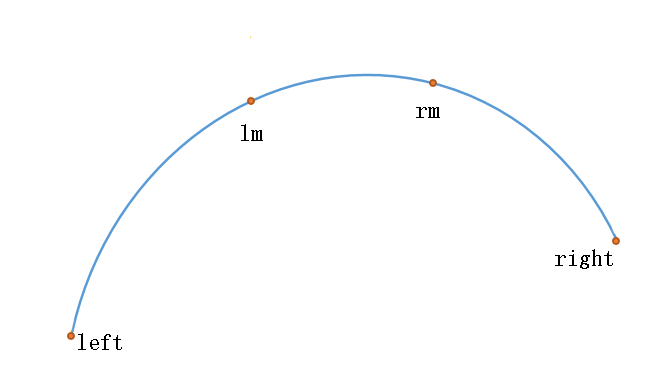
如图这种情况先减后增有极小,若lm比rm低(即lm对应的函数值 < rm函数值)则极小点(图中最低点)肯定在[ left, rm ] ,反之在[ lm, right ],剩下就跟二分一样根据大小关系调整区间就行了。那lm和rm取值多少?一个不错的取值是lm为整个区间的1/3点,rm为2/3点,即
lmid = l + (r - l)/3; rmid = r - (r - l)/3;
嗯三分就这样完了。
然后另外一种情况,先增后减有极大:
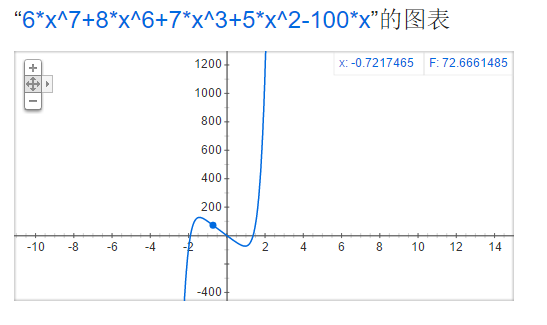
HDU 2899 Strange fuction
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
double y;
double val(double x){
return 6*x*x*x*x*x*x*x+8*x*x*x*x*x*x+7*x*x*x+5*x*x-y*x;
}
double solve(double l,double r){
double eps = 1e-7;
while(l + eps < r){
double lmid = l + (r-l)/3,rmid = r - (r-l)/3;
if(val(lmid) < val(rmid)){
r = rmid;
}else{
l = lmid;
}
}
return val(l);
}
int main(){
int t;
cin>>t;
while(t--){
cin>>y;
printf("%.4f
", solve(0,100.0));
}
return 0;
}
有一条抛物线y=ax^2+bx+c和一个点P(x,y),求点P到抛物线的最短距离d。 输入 第1行:5个整数a,b,c,x,y。前三个数构成抛物线的参数,后两个数x,y表示P点坐标。-200≤a,b,c,x,y≤200 输出 第1行:1个实数d,保留3位小数(四舍五入) 样例输入 2 8 2 -2 6 样例输出 2.437
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
#define clr( a , x ) memset ( a , x , sizeof (a) );
#define RE freopen("1.in","r",stdin);
#define WE freopen("1.out","w",stdout);
#define SpeedUp std::cout.sync_with_stdio(false);
const int maxn = 1e5+5;
const int inf = 0x3f3f3f3f;
double a,b,c,x,y;
double val(double X){
return sqrt((X-x)*(X-x)+(a*X*X+b*X+c-y)*(a*X*X+b*X+c-y));
}
double solve(double l,double r){
double eps = 1e-5;
while(l+eps<r){
double lmid = l + (r-l)/3,rmid = r - (r-l)/3;
if(val(lmid) < val(rmid)){
r = rmid;
}else{
l = lmid;
}
}
return val(l);
}
int main(){
// RE
while(cin>>a>>b>>c>>x>>y){
printf("%.3f
", solve(-200.0,200.0));
}
return 0;
}