FZU 1078 计算循环冗余码【模拟】

计算机网络中采用循环冗余码来校验数据的正确性。其原理是:发送方计算出待发送的二进制数据的循环冗余码，并随同原数据一起发送到接收方；接收方通过重新计算接收到的数据的循环冗余码，并和收到的循环冗余码进行比较，如果两者相同则可判定所收到的数据是正确的，否则说明数据是错误的。其中计算二进制数据的循环冗余码的计算过程如下：

1.协议事先约定一个二进制生成表达式，本题设为10011；
2.将待发送的二进制数据串的末尾加4个0；
3.将补上0的数据串按模2除法除于生成表达式，取余数；
4.该余数就是该二进制数据串的循环冗余码。

例如: 

数据串为：1101011011
生成表达式为：10011
循环冗余码为：1110

计算过程如下： 

根据上述的计算方法，请编写一个循环冗余码计算程序，假设二进制数据串的长度不超过20位，生成表达式固定为10011。

Input

输入的第一行含一个正整数k (1<=k<=10)，表示测试例的个数。后面紧接着k行，每行对应一个测试例，含一个N位二进制串(1<=N<=20)，代表数据。

Output

每个测试例对应一行输出，含一个5位二进制串，表示循环冗余码。

Sample Input

2
1101011011
10101010

Sample Output

01110
01001

---

【分析】：首先要了解循环冗余校验码是什么。

循环冗余校验码是通过除法运算来建立有效信息位和校验位之间的约定关系。假定，待编码的有效信息以多项式M（X）表示，将它左移若干位后，用另一个约定的多项式G（X）去除，所产生的余数就是校验位。有效信息位与校验位相拼接就构成了CRC码。当接收方收到发来的CRC码后，他仍用约定的多项式G（X）去除，若余数为0，表明该代码接收无误；若余数不为0，表明某一位出错，再进一步由余数值确定出错的位置，并予以纠正。

循环冗余校验码的编码方法：

循环冗余校验码由两部分组成，左边为信息位，右边为校验位。若信息位为N位，校验位为K位，则该校验码被称为（N＋K，N）码。

这里，需介绍一下模2的运算规则。模2运算不考虑加法的进位和减法的借位，即0±0＝0，0±1＝1，1±0＝1，1±1＝0。作模2除法时，上商的原则是当部分余数首位是1时（即使被除数比除数小），商取1，反之商取0，然后按模2加减求得余数。当被除数逐步除完时，最终的余数比除数少一位，此余数就是校验位。

对“模2除法”进行说明：

“模2除法”与“算术除法”类似，但它既不向上位借位，也不比较除数和被除数的相同位数值的大小，只要以相同位数进行相除即可。模2加法运算为：1+1=0，0+1=1，0+0=0，无进位，也无借位；模2减法运算为：1-1=0，0-1=1，1-0=1，0-0=0，也无进位，无借位。相当于二进制中的逻辑异或运算。

g(x)和h(x)的除运算，可以通过g和h做xor（异或）运算。二进制相除就是一个异或的过程。比如将11001与10101做xor运算：

      

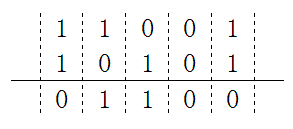
明白了xor运算法则后，举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1，既h是9位的二进制串111010101。 

经过迭代运算后，最终得到的r是10001100，这就是CRC效验码。

【代码】：明白原理后就是简单模拟。

#include <iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<streambuf>
#include<cmath>
#include<string>
using namespace std;
#define ll long long
#define oo 10000000

int n,m;
char b[]="10011";
int main()
{
    string a;
    int t;
    scanf("%d",&t);
    while(t--)
    {
        cin>>a;
        a=a+"0000";
        for(int i=0;i<a.size()-4;i++)
        {
            if(a[i]=='0')
            {
                continue;
            }
            int p=i;
            for(int j=0;j<5;j++,p++)
            {
                if(a[p]^b[j])
                    a[p]='1';
                else
                    a[p]='0';
            }
        }
        for(int i=a.size()-5;i<a.size();i++)
            printf("%c",a[i]);
        printf("
");
    }
    return 0;
}