Mike is trying rock climbing but he is awful at it.
There are n holds on the wall, i-th hold is at height ai off the ground. Besides, let the sequence aiincrease, that is, ai < ai + 1 for all i from 1 to n - 1; we will call such sequence a track. Mike thinks that the track a1, ..., an has difficulty 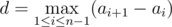 . In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
. In other words, difficulty equals the maximum distance between two holds that are adjacent in height.
Today Mike decided to cover the track with holds hanging on heights a1, ..., an. To make the problem harder, Mike decided to remove one hold, that is, remove one element of the sequence (for example, if we take the sequence (1, 2, 3, 4, 5) and remove the third element from it, we obtain the sequence(1, 2, 4, 5)). However, as Mike is awful at climbing, he wants the final difficulty (i.e. the maximum difference of heights between adjacent holds after removing the hold) to be as small as possible among all possible options of removing a hold. The first and last holds must stay at their positions.
Help Mike determine the minimum difficulty of the track after removing one hold.
The first line contains a single integer n (3 ≤ n ≤ 100) — the number of holds.
The next line contains n space-separated integers ai (1 ≤ ai ≤ 1000), where ai is the height where the hold number i hangs. The sequence ai is increasing (i.e. each element except for the first one is strictly larger than the previous one).
Print a single number — the minimum difficulty of the track after removing a single hold.
3
1 4 6
5
5
1 2 3 4 5
2
5
1 2 3 7 8
4
In the first sample you can remove only the second hold, then the sequence looks like (1, 6), the maximum difference of the neighboring elements equals 5.
In the second test after removing every hold the difficulty equals 2.
In the third test you can obtain sequences (1, 3, 7, 8), (1, 2, 7, 8), (1, 2, 3, 8), for which the difficulty is 4, 5 and 5, respectively. Thus, after removing the second element we obtain the optimal answer — 4.
【题意】:对一个数组,定义困难值是两个相邻元素之间差的最大值。
现在又一个数组,可以去掉任意一个元素,问剩余数列的困难值的最小值是多少。
【分析】:由于数据小,可以枚举去掉的元素然后暴力更新,复杂度是 O(nn)。如果数据比较大的话,可以利用动态规划O(n)过。
【代码】:
#include <bits/stdc++.h>
#define N 100010
using namespace std;
#define oo 99999
int a[110];
int b[110];
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int ans=oo;
for(int i=2;i<n;i++){
int k=0;
for(int j=1;j<=n;j++){
if(j==i)continue;
b[k++]=a[j];
}
int MAX=0;
for(int j=0;j<n-1;j++){
MAX=max(MAX,b[j+1]-b[j]);
}
ans=min(ans,MAX);
}
cout<<ans<<endl;
return 0;
}