HashMap+双向链表手写LRU缓存算法/页面置换算法

import java.util.Hashtable;

class DLinkedList {
    String key; //键
    int value;    //值
    DLinkedList pre; //双向链表前驱
    DLinkedList next; //双向链表后继
}
public class LRUCache {
    private Hashtable<String,DLinkedList> cache = new Hashtable<String,DLinkedList>(); 
    private int count;
    private int capacity;
    private DLinkedList head, tail;
    public LRUCache(int capacity) {
        this.count = 0;
        this.capacity = capacity;
        head = new DLinkedList();
        head.pre = null;
        tail = new DLinkedList();
        tail.next = null;
        
        head.next = tail;
        tail.pre = head;
    }
    public int get(String key) {
        DLinkedList node = cache.get(key);
        if(node == null) return -1;
        this.moveToHead(node);
        return node.value;
    }
    public void set(String key,int value) {
        DLinkedList node = cache.get(key);
        if(node == null) {
            DLinkedList newNode = new DLinkedList();
            newNode.key = key;
            newNode.value = value;
            this.cache.put(key, newNode);
            this.addNode(newNode);
            ++count;
        
            if(count>capacity) {
                DLinkedList tail = this.popTail();
                this.cache.remove(tail.key);
                --count;
            }
        }
        else {
            node.value = value;
            this.moveToHead(node);
        }
    }
    private void addNode(DLinkedList node) {
        node.pre = head;
        node.next = head.next;
        head.next.pre = node;
        head.next = node;
    }
    private void removeNode(DLinkedList node) {
        DLinkedList pre = node.pre;
        DLinkedList next = node.next;
        pre.next = next;
        next.pre = pre;
    }
    private void moveToHead(DLinkedList node) {
        this.removeNode(node);
        this.addNode(node);
    }
    private DLinkedList popTail() {
        DLinkedList res = tail.pre;
        this.removeNode(res);
        return res;
    }
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        DLinkedList node = head;
        while(node != null){
            sb.append(String.format("%s:%s ", node.key,node.value));
            node = node.next;
        }
        return sb.toString();
    }
    public static void main(String[] args) {
        LRUCache lru = new LRUCache(3);
        lru.set("1", 7);
        System.out.println(lru.toString());
        lru.set("2", 0);
        System.out.println(lru.toString());
        lru.set("3", 1);
        System.out.println(lru.toString());
        lru.set("4", 2);
        System.out.println(lru.toString());
        lru.get("2");
        System.out.println(lru.toString());
        lru.set("5", 3);
        System.out.println(lru.toString());
        lru.get("2");
        System.out.println(lru.toString());
        lru.set("6", 4);
        System.out.println(lru.toString());
        /*
         0ull:0 1:7 null:0 
        null:0 2:0 1:7 null:0 
        null:0 3:1 2:0 1:7 null:0 
        null:0 4:2 3:1 2:0 null:0 
        null:0 2:0 4:2 3:1 null:0 
        null:0 5:3 2:0 4:2 null:0 
        null:0 2:0 5:3 4:2 null:0 
        null:0 6:4 2:0 5:3 null:0  
         */
    }
}

那么如何设计一个LRU缓存，使得放入和移除都是 O(1) 的，我们需要把访问次序维护起来，但是不能通过内存中的真实排序来反应，有一种方案就是使用双向链表。

整体的设计思路是，可以使用 HashMap 存储 key，这样可以做到 save 和 get key的时间都是 O(1)，而 HashMap 的 Value 指向双向链表实现的 LRU 的 Node 节点，如图所示。

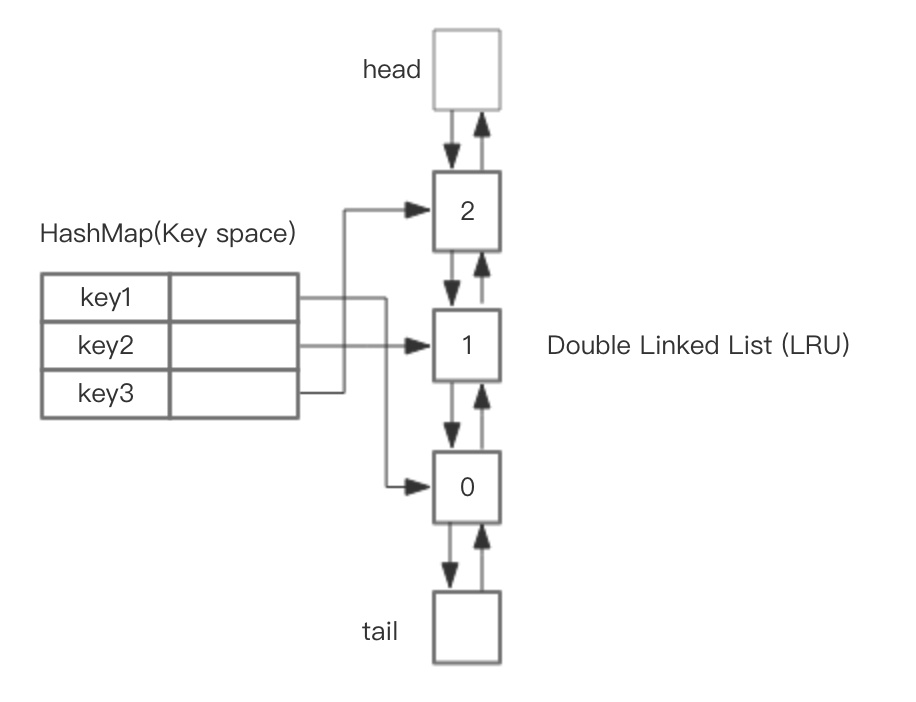
LRU 存储是基于双向链表实现的，下面的图演示了它的原理。其中 head 代表双向链表的表头，tail 代表尾部。首先预先设置 LRU 的容量，如果存储满了，可以通过 O(1) 的时间淘汰掉双向链表的尾部，每次新增和访问数据，都可以通过 O(1)的效率把新的节点增加到对头，或者把已经存在的节点移动到队头。

下面展示了，预设大小是 3 的，LRU存储的在存储和访问过程中的变化。为了简化图复杂度，图中没有展示 HashMap部分的变化，仅仅演示了上图 LRU 双向链表的变化。我们对这个LRU缓存的操作序列如下：

save("key1", 7)

save("key2", 0)

save("key3", 1)

save("key4", 2)

get("key2")

save("key5", 3)

get("key2")

save("key6", 4)

相应的 LRU 双向链表部分变化如下：

s = save, g = get

总结一下核心操作的步骤:

1. save(key, value)，首先在 HashMap 找到 Key 对应的节点，如果节点存在，更新节点的值，并把这个节点移动队头。如果不存在，需要构造新的节点，并且尝试把节点塞到队头，如果LRU空间不足，则通过 tail 淘汰掉队尾的节点，同时在 HashMap 中移除 Key。
2. get(key)，通过 HashMap 找到 LRU 链表节点，因为根据LRU 原理，这个节点是最新访问的，所以要把节点插入到队头，然后返回缓存的值。

【https://zhuanlan.zhihu.com/p/34133067】