计算点到直线的距离】 C#实现

如下图所示，我们要计算的是c点到直线ab的距离。

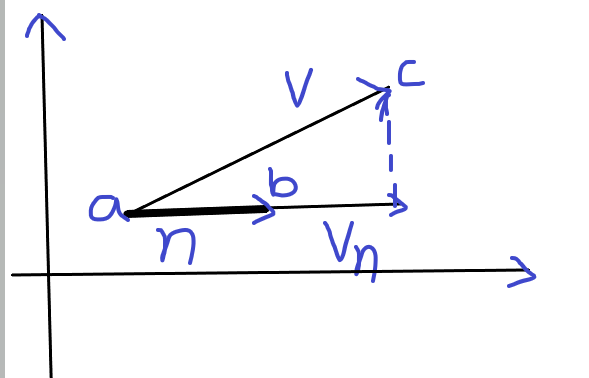
首先我们要认识到，虽然在数学上，【点】与【向量】是两种不同的名词，但在实际的计算中是可以直接把【点】的坐标视为从坐标系【原点】到【点】的【向量】。有了这个前提，线段ab其实可以简单地表示为向量n，其他的向量同理可得。用向量解决这个问题的关键是求出v在n上的投影向量v_n。

　　　　　　　　　　　　　　　　　　　　经过推导，得到等式 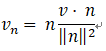（注意【点乘】和【乘以】的区别）

　　　　　　　　　　　　　　　　　　　　为了便于计算，可以把等式写为这样 

【点乘】的计算优先级高于【乘以】，所以该等式是通过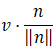计算出投影向量v_n的【模】，然后再乘以n的标准化向量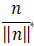也就是v_n的方向，最后得到v_n

。前面提到过，【点】和【向量】可视为等价的，也就是说【向量】也可以代表【点】的坐标，所以求出了v_n，也就等价于求出了c到ab的垂线与ab（ab的延长线）相交的点的坐标。然后我们利用两点间的距离公式即可以求出c到ab的距离。下面直接上代码。

using System;
using System.Numerics;

namespace _3dMath
{
    class VectorCalculate{
        
        public VectorCalculate(Vector3 point_a, Vector3 point_b, Vector3 point_c)
        {
            _point_a = point_a;
            _point_b = point_b;
            _point_c = point_c;
        }

        public float DistanceCalculate()
        {
            Vector3 vec_ab = _point_b - _point_a;
            Vector3 vec_ac = _point_c - _point_a;
            float distance = 0.0f;
            Vector3 vec_Normalize = Vector3.Normalize(vec_ab);
            float projection_length = Vector3.Dot(vec_ac, vec_Normalize); //计算出投影向量的模
            Vector3 vec_Projection = Vector3.Multiply(projection_length, vec_Normalize); //计算出投影向量
            distance = Vector3.Distance(vec_ac, vec_Projection);
            return distance;
        } 

        private Vector3 _point_a;
        private Vector3 _point_b;
        private Vector3 _point_c;
    }

    class Test{
        static void Main(string[] arg)
        {
            Vector3 point_a = new Vector3(1.0f, 1.0f, 1.0f);
            Vector3 point_b = new Vector3(5.0f, 2.0f, 1.0f);
            Vector3 point_c = new Vector3(2.0f, 3.0f, 1.0f);
            //Vector3 point_c = new Vector3(-1.0f, 2.0f, 0.0f); 
            VectorCalculate vec_Calculate = new VectorCalculate(point_a, point_b, point_c);
            float res = vec_Calculate.DistanceCalculate();
            Console.WriteLine("The distance is: {0}", res);
        }
    }
}

最后，如果各位发现内容有不严谨的地方，希望能够在评论区指出，欢迎讨论。