个人代码约定
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void solve() {
// 编写核心代码
}
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
solve();
return 0;
}
A:美丽的 2
本题总分:5 分
【问题描述】
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴。
他很好奇,在公元 1 年到公元 2020 年(包含)中,有多少个年份的数位中包含数字 2?
void solve() {
int cnt = 0;
for (int i = 2; i <= 2020; ++i) {
int j = i;
while (j) {
if (j % 10 == 2) {
cnt++;
break;
}
j /= 10;
}
}
cout << cnt; //563
}
B:扩散
本题总分:5 分
【题目描述】
小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图,每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点:(0, 0), (2020, 11), (11, 14), (2000, 2000)。
只有这几个格子上有黑色,其它位置都是白色的。
每过一分钟,黑色就会扩散一点。具体的,如果一个格子里面是黑色,它就会扩散到上、下、左、右四个相邻的格子中,使得这四个格子也变成黑色(如果原来就是黑色,则还是黑色)。
请问,经过 2020 分钟后,画布上有多少个格子是黑色的。
跑BFS,时间在2020内都记录,边记录边累计个数,每个加个2100,从0开始,一分钟向上扩散1,最多不超过2100
// 20312088
struct node {
int x, y, t;
};
int nx[4] = {1, 0, -1, 0};
int ny[4] = {0, 1, 0, -1};
int e[10000][10000];
bool vis[10000][10000];
queue<node> q;
int n = 2100;
void solve() {
node s, p;
p.t = 0, p.x = n, p.y = n;
q.push(p);
p.t = 0, p.x = n + 2000, p.y = n + 2000;
q.push(p);
p.t = 0, p.x = n + 2020, p.y = n + 11;
q.push(p);
p.t = 0, p.x = n + 11, p.y = n + 14;
q.push(p);
vis[n][n] = vis[n + 2000][n + 2000] = vis[n + 2020][n + 11] = vis[n + 11][n + 14] = 1;
ll ans = 4;
while (q.size()) {
p = q.front(), q.pop();
for (int i = 0; i < 4; ++i) {
s.x = p.x + nx[i];
s.y = p.y + ny[i];
s.t = p.t + 1;
if (vis[s.x][s.y] == false and s.t <= 2020) {
vis[s.x][s.y] = true;
ans++;
q.push(s);
}
}
}
cout << ans << "
";
}
C阶层约数
本题总分:10 分
【问题描述】
定义阶乘 n! = 1 × 2 × 3 × · · · × n。
请问 100! (100 的阶乘)有多少个约数。
思路:就是简单的分解因数:(5! = 1 imes2 imes3 imes4 imes5=2^3 imes3^1 imes5^1)
using ll = long long;
void solve() {
ll cnt[110] = {0};
for (int i = 1; i <= 100; ++i) {
int tmp = i;
for (int j = 2; j <= i; ++j)
while (tmp % j == 0) {
tmp /= j;
cnt[j]++;
}
}
ll ans = 1;
for (int i = 1; i <= 100; ++i) ans *= (cnt[i] + 1);
cout << ans << "
";
}
D:本质上升序列
本题总分:10 分
【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
思路:
// 3616159 写法比较暴力,输出要等一会
using ll = long long;
map<string, int> vis;
void solve() {
queue<pair<string, int>> q;
string s = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
ll ans = 0;
for (int i = 0; i < s.size(); ++i) {
string tmp = "";
tmp += s[i];
if (!vis[tmp]) {
vis[tmp] = 1;
q.push({tmp, i});
++ans;
}
}
while (q.size()) {
string t = q.front().first;
int pos = q.front().second;
q.pop();
for (int i = pos + 1; i < s.size(); ++i)
if (s[i] > s[pos] and !vis[t + s[i]]) {
vis[t + s[i]] = 1;
q.push({t + s[i], i});
++ans;
}
}
cout << ans << "
";
}
试题 E: 玩具蛇
本题总分:15 分
【问题描述】
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
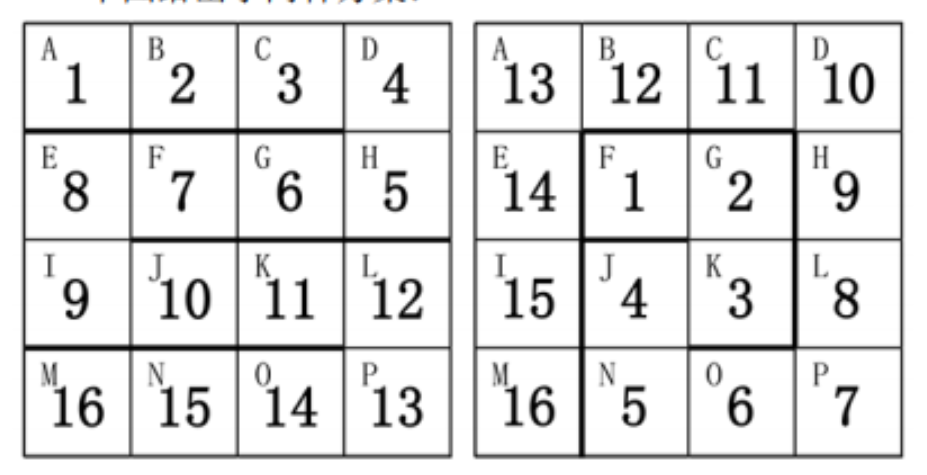
思路:dfs各个找一遍,实话说,这题好像比前面简单。。
// 552
using ll = long long;
int vis[5][5];
int nexti[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
ll ans = 0;
void dfs(int x, int y, int count) {
if (x >= 4 || x < 0 || y >= 4 || y < 0) return;
if (count == 16) {
ans++;
}
for (int i = 0; i < 4; i++) {
int nx = x + nexti[i][0];
int ny = y + nexti[i][1];
if (!vis[nx][ny]) {
vis[nx][ny] = 1;
dfs(nx, ny, count + 1);
vis[nx][ny] = 0;
}
}
}
void solve() {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
vis[i][j] = 1;
dfs(i, j, 1);
vis[i][j] = 0;
}
}
cout << ans;
}
F: 皮亚诺曲线距离
【问题描述】
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形,它是从左下角出发,经过一个 3 × 3 的方格中的每一个格子,最终到达右上角的一条曲线。
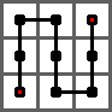
下图给出了皮亚诺曲线的 2 阶情形,它是经过一个 32 × 32 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
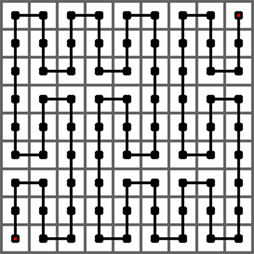
下图给出了皮亚诺曲线的 3 阶情形,它是经过一个 33 × 33 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
我们将这些格子放到坐标系中,对于 k 阶皮亚诺曲线,左下角的坐标是(0, 0),右上角坐标是 (3k − 1, 3k − 1),右下角坐标是 (3k − 1, 0),左上角坐标是(0, 3k − 1)。
给定 k 阶皮亚诺曲线上的两个点的坐标,请问这两个点之间,如果沿着皮亚诺曲线走,距离是多少?
【输入格式】
输入的第一行包含一个正整数 k,皮亚诺曲线的阶数。第二行包含两个整数 x1, y1,表示第一个点的坐标。
第三行包含两个整数 x2, y2,表示第二个点的坐标。
【输出格式】
输出一个整数,表示给定的两个点之间的距离。
【样例输入】
1
0 0
2 2
【样例输出】
8
【样例输入】
2
0 2
0 3
【样例输出】
13
【评测用例规模与约定】
对于 30% 的评测用例,(0 ≤ k ≤ 10)。
对于 50% 的评测用例,(0 ≤ k ≤ 20)。
对于所有评测用例,(0 ≤ k ≤ 100, 0 ≤ x1, y1, x2, y2 < 3k, x1, y1, x2, y2 ≤ 10^{18})。
数据保证答案不超过 (10^{18})没怎么看懂题,跳过了
G: 游园安排
【问题描述】
L 星球游乐园非常有趣,吸引着各个星球的游客前来游玩。小蓝是 L 星球游乐园的管理员。
为了更好的管理游乐园,游乐园要求所有的游客提前预约,小蓝能看到系统上所有预约游客的名字。每个游客的名字由一个大写英文字母开始,后面跟0 个或多个小写英文字母。游客可能重名。
小蓝特别喜欢递增的事物。今天,他决定在所有预约的游客中,选择一部分游客在上午游玩,其他的游客都在下午游玩,在上午游玩的游客要求按照预约的顺序排列后,名字是单调递增的,即排在前面的名字严格小于排在后面的名字。
一个名字 A 小于另一个名字 B 是指:存在一个整数 i,使得 A 的前 i 个字母与 B 的前 i 个字母相同,且 A 的第 i+1 个字母小于 B 的第 i+1 个字母。(如果 A 不存在第 i + 1 个字母且 B 存在第 i + 1 个字母,也视为 A 的第 i + 1 个字母小于 B 的第 i + 1 个字母)
作为小蓝的助手,你要按照小蓝的想法安排游客,同时你又希望上午有尽量多的游客游玩,请告诉小蓝让哪些游客上午游玩。如果方案有多种,请输出上午游玩的第一个游客名字最小的方案。如果此时还有多种方案,请输出第一个游客名字最小的前提下第二个游客名字最小的方案。如果仍然有多种,依此类推选择第三个、第四个……游客名字最小的方案。
【输入格式】
输入包含一个字符串,按预约的顺序给出所有游客的名字,相邻的游客名字之间没有字符分隔。
【输出格式】
按预约顺序输出上午游玩的游客名单,中间不加任何分隔字符。
【样例输入】
WoAiLanQiaoBei
【样例输出】
AiLanQiao
【评测用例规模与约定】
对于 20% 的评测数据,输入的总长度不超过 20 个字母。
对于 50% 的评测数据,输入的总长度不超过 300 个字母。
对于 70% 的评测数据,输入的总长度不超过 10000 个字母。
对于所有评测数据,每个名字的长度不超过 10 个字母,输入的总长度不超
过 1000000 个字母。
思路:排个顺序,比较字母个数,小字母多的放前面,一样多的,小字母靠前放前面
写法有点暴力,不能保证AC 100%数据
string x[1000001];
bool cmp(string a, string b) {
int visa[30] = {0}, visb[30] = {0};
visa[a[0] - 'A']++;
visb[b[0] - 'A']++;
for (int i = 1; i < a.length(); i++)
visa[a[i] - 'a']++;
for (int i = 1; i < b.length(); i++)
visb[b[i] - 'a']++;
int mn = min(a.length(), b.length());
for (int i = 0; i < mn; i++) {
if (visa[i] > visb[i]) return 1;
else if (visa[i] < visb[i])
return 0;
}
if (a.length() > b.length()) return 0;
else if (a.length() < b.length())
return 1;
else {
for (int i = 0; i < mn; i++)
if (a[i] > b[i]) return 0;
else if (a[i] < b[i])
return 1;
return 1;
}
}
void solve() {
string ch;
cin >> ch;
int i = 0;
int n = -1;
while (i <= ch.size()) {
if (ch[i] >= 'A' and ch[i] <= 'Z') {
n++;
x[n] += ch[i];
} else if (ch[i] != '�')
x[n] += ch[i];
++i;
}
n++;
sort(x, x + n, cmp);
for (int i = 0; i <= n / 2; ++i) cout << x[i];
cout << "
";
}
H: 答疑
【问题描述】
有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。老师可以安排答疑的顺序,同学们要依次进入老师办公室答疑。
一位同学答疑的过程如下:
首先进入办公室,编号为 i 的同学需要 si 毫秒的时间。
然后同学问问题老师解答,编号为 i 的同学需要 ai 毫秒的时间。
答疑完成后,同学很高兴,会在课程群里面发一条消息,需要的时间可 以忽略。
最后同学收拾东西离开办公室,需要 ei 毫秒的时间。一般需要 10 秒、20 秒或 30 秒,即 ei 取值为 10000,20000 或 30000。
一位同学离开办公室后,紧接着下一位同学就可以进入办公室了。
答疑从 0 时刻开始。老师想合理的安排答疑的顺序,使得同学们在课程群里面发消息的时刻之和最小。
【输入格式】
输入第一行包含一个整数 n,表示同学的数量。
接下来 n 行,描述每位同学的时间。其中第 i 行包含三个整数 si, ai, ei,意义如上所述。
【输出格式】
输出一个整数,表示同学们在课程群里面发消息的时刻之和最小是多少。
【样例输入】
3
10000 10000 10000
20000 50000 20000
30000 20000 30000
【样例输出】
280000
【样例说明】
按照 1, 3, 2 的顺序答疑,发消息的时间分别是 20000, 80000, 180000。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ n ≤ 20。
对于 60% 的评测用例,1 ≤ n ≤ 200。
对于所有评测用例,1 ≤ n ≤ 1000,1 ≤ si ≤ 60000,1 ≤ ai ≤ 1000000,ei ∈ {10000, 20000, 30000},即 ei 一定是 10000、20000、30000 之一。
思路:s+e+a小的放前面,一样的就把s+a小的放前面
写法有点暴力,不能保证AC 100%数据
using ll = long long;
struct student {
ll s, a, e;
} stu[1001];
bool cmp(const student n1, const student n2) {
ll sum1 = n1.s + n1.a, sum2 = n2.s + n2.a;
if (sum1 + n1.e > sum2 + n2.e) return 0;
else if (sum1 + n1.e < sum2 + n2.e)
return 1;
else {
if (sum1 > sum2) return 0;
else if (sum1 < sum2)
return 1;
else
return 1;
}
}
void solve() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> stu[i].s >> stu[i].a >> stu[i].e;
}
sort(stu, stu + n, cmp);
ll ans = 0, k = 0;
for (int i = 0; i < n; i++) {
k = k + stu[i].s + stu[i].a;
ans += k;
k += stu[i].e;
}
cout << ans << endl;
}
I: 出租车
待补
J: 质数行者
待补