补题链接:Here
DFS序列 (非树形DP),这道题成功被骗...
贴一下学姐讲解:
这个题表面上看起来像是个 树上dp,但是你会发现,当xy同色的时候要求x到y的路径上所有点颜色一样这个事情非常难办——如果我们考虑颜色一个一个的涂,同色这个条件父亲节点有三个子树为例,可能其中两个子树和这个父亲节点是同样的颜色,而另外一个子树是另一个颜色,这就非常难办了。
我们考虑把树上的东西转化到线性结构上——这样的操作当然是使用dfs序啦。
----------------------以下是介绍dfs序的分割线-----------------------
dfs序:每个节点在dfs深度优先遍历中的进出栈的时间序列(为了方便接下来的操作我们往往有两种不同的写法,一种是只记录进栈顺序,一种是进栈出栈都记录,视题目的具体情况而定怎么写。)
简单来说:DFS 序列是指 DFS 调用过程中访问的节点编号的序列。

一般来讲,我们需要的不仅仅有这个进出栈的顺序序列,还有每个点在第几个进栈这个信息——点x在第几个进栈就是这个点的时间戳,一般记为dfn[x] (时间戳在强连通分量 tarjan算法 里也有很巧妙的运用)。
正如图上所说,第二种dfs序两个相同数字之间就是这个点的子树,而其实在第一种方法中你也可以用个数组记录它出栈的之前最后一个进栈的点,也就是当前访问过的点里面时间戳最大的是哪一个,这样也可也得到这个点对应的子树是在哪一个区间里了。将来你就可以通过诸如在这个树上建线段树的操作实现对子树的一些修改的维护,比如说子树所有点的权值加一个数,就很美滋滋了(这个以后有机会再讲)。
稍微注意一点,在一般的树中(二叉树 除外)一个节点的儿子是没有左右顺序的可以随便先访问哪个,所以,一棵树的dfs序是可能有很多种的。
------------------------下面回到本题--------------------------------------
如果我们用dfs序来表示这棵树,并且按dfs序来一个一个点涂色的话,我们就可以把问题从树上转化到链上,问题也许会简单许多。
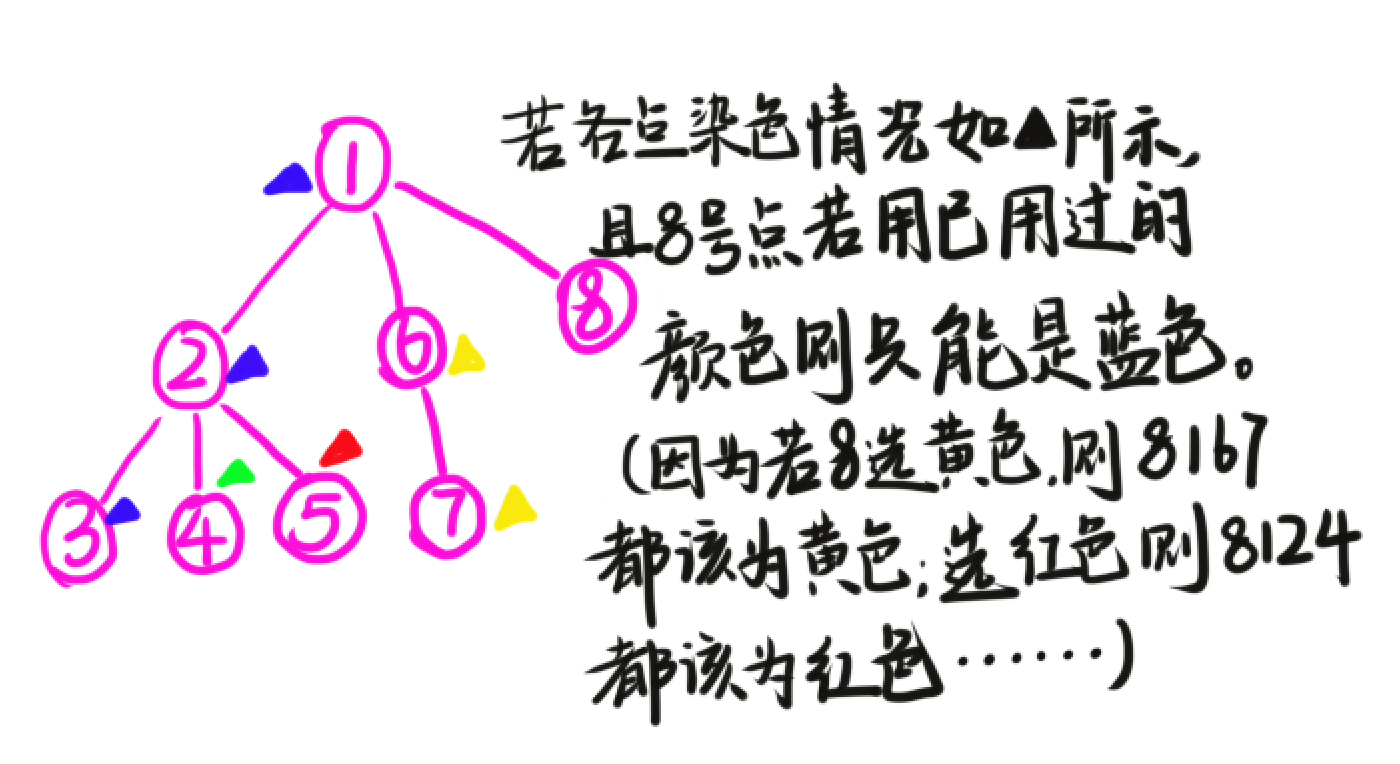
我们会发现,如果我们按dfs序涂色,在涂每一个点之前,他的父亲祖父等祖先节点肯定都已经先涂过了(这些点的dfs序都比当前点小),他的兄弟节点(也包括各种或近或远的“堂兄弟”节点)和兄弟节点的子树也许也涂过一些。涂这个点无非是两种选择:涂一种新的颜色,或者涂一种已经用过的颜色。涂一种新的颜色自然是没用过的颜色都可以。而涂一种已经用过的颜色的话,这个点的颜色必须和他父亲的颜色一样,因为这个点到之前的所有点的路径都是要经过它父亲的,如果他和父亲不同色,他和他同色那个点的路径上就不可能所有点颜色都一样,至少他父亲就是不同的。也就是说涂一种已经用过的颜色其实只有一种方案——和父亲相同。
于是我们发现,算涂法个数其实并不需要关心这棵树长什么样,我们就按照dfs序一个一个涂就可以了,用f[i] [j] 表示树上dfs序的前i个点用了j种颜色的方法数:
using ll = long long;
const int mod = 1e9 + 7;
ll dp[310][310];
void solve() {
ll n, k, ans = 0;
cin >> n >> k;
dp[0][0] = 1;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= k; ++j)
dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - 1] * (k - j + 1) % mod) % mod;
for (int i = 1; i <= k; ++i) ans = (ans + dp[n][i]) % mod;
cout << ans;
}