A题:走廊泼水节
链接:https://ac.nowcoder.com/acm/contest/1056/A
题目描述
给定一棵N个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。
输入描述:
第一行包含整数t,表示共有t组测试数据。
对于每组测试数据,第一行包含整数N。
接下来N-1行,每行三个整数X,Y,Z,表示X节点与Y节点之间存在一条边,长度为Z。
输出描述:
每组数据输出一个整数,表示权值总和最小值。
每个结果占一行。
示例1
输入
2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5
输出
4
17
备注:
\[N <= 6000 , Z <= 100
\]
例解释
第一组数据,在 22 和 33 之间修建一条长度为 44 的道路,
使这棵树变成一个完全图,且原来的树依然是这个图的唯一最小生成树.
题解
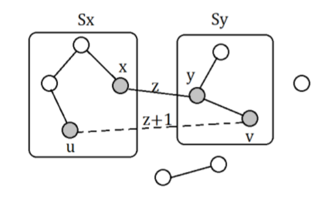
- 对给定树上的 \(N−1\) 条边模拟一遍\(Kruskal\)
- 通过边$(x,y) $合并两个并查集
- xx 集合中的每个点到 \(y\) 集合中的每个点
- 添加一条长度为 $w(x,y)+1 $的边
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 6010
struct edge{ int u,v,w; }e[maxn];
int t,n,f[6010],s[6010];
long long ans;
bool cmp(edge x,edge y){ return x.w<y.w; }
int find(int x){
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(int i=1;i<=n;++i){ f[i]=i; s[i]=1; }
for(int i=1;i<n;++i) scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);
sort(e+1,e+n,cmp);
ans=0;
for(int fu,fv,i=1;i<n;++i){
fu=find(e[i].u); fv=find(e[i].v);
if(fu==fv) continue;
ans+=1ll*(e[i].w+1)*(s[fu]*s[fv]-1);
f[fu]=fv;
s[fv]+=s[fu];
}
printf("%lld\n",ans);
}
return 0;
}
B题:Picnic Planning (控制度数的最小生成树,DFS)
https://ac.nowcoder.com/acm/contest/1056/B
#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_Bstdio(false);cin.tie(0); cout.tie(0)
typedef long long ll;
inline int read() {
int s = 0, w = 1; char ch = getchar();
while (ch < 48 || ch > 57) { if (ch == '-') w = -1; ch = getchar(); }
while (ch >= 48 && ch <= 57) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();
return s * w;
}
const int N = 37;
const int INF = 0x3f3f3f3f;
struct Edge {
int x, y, z;
bool operator < (const Edge w) const {
return z < w.z;
}
}f[N];
int n, k, tot, ans, a[N][N], fa[N], d[N], v[N];
map<string, int> mp;
vector<Edge> e;
bool b[N][N];
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void dfs(int x, int pre) {
for (int i = 2; i <= tot; ++i) {
if (i == pre || !b[x][i]) continue;
if (f[i].z == -1) {
if (f[x].z > a[x][i]) f[i] = f[x];
else {
f[i].x = x;
f[i].y = i;
f[i].z = a[x][i];
}
}
dfs(i, x);
}
}
int main() {
js;
memset(a, 0x3f, sizeof(a));
memset(d, 0x3f, sizeof(d));
mp["Park"] = tot = 1;
for (int i = 1; i < N; ++i) fa[i] = i;
cin >> n;
for (int i = 1; i <= n; ++i) {
Edge w;
string s1, s2;
cin >> s1 >> s2 >> w.z;
w.x = mp[s1] ? mp[s1] : (mp[s1] = ++tot);
w.y = mp[s2] ? mp[s2] : (mp[s2] = ++tot);
e.push_back(w);
a[w.x][w.y] = a[w.y][w.x] = min(a[w.x][w.y], w.z);
}
cin >> k;
sort(e.begin(), e.end());
for (auto it : e) { //去掉1的连边,构成几个连通块,再把连通块并成一个求解花费
if (it.x == 1 || it.y == 1) continue;
int fax = find(it.x), fay = find(it.y);
if (fax != fay) {
fa[fax] = fay;
b[it.x][it.y] = b[it.y][it.x] = 1;
ans += it.z;
}
}
for (int i = 2; i <= tot; ++i) //找连通区域内和1连接花费最小
if (a[1][i] != INF) {
int rt = find(i);
if (d[rt] > a[1][i]) {
v[rt] = i;
d[rt] = a[1][v[rt]];
}
}
for (int i = 1; i <= tot; ++i) { //先把连通区域和1连接
if (d[i] != INF) {
--k;
b[1][v[i]] = b[v[i]][1] = 1;
ans += a[1][v[i]];
}
}
while (k--) { //调整看能不能更小一点
memset(f, -1, sizeof(f));
f[1].z = -INF;
for (int i = 2; i <= tot; ++i)
if (b[1][i]) f[i].z = -INF;
dfs(1, 0);
int o, w = -INF;
for (int i = 2; i <= tot; ++i)
if (w < f[i].z - a[1][i]) {
o = i;
w = f[i].z - a[1][o];
}
if (w <= 0) break;
b[1][o] = b[o][1] = 1;
b[f[o].x][f[o].y] = b[f[o].y][f[o].x] = 0;
ans -= w;
}
cout << "Total miles driven: " << ans << endl;
return 0;
}
C题:最优比率生成树
https://ac.nowcoder.com/acm/contest/1056/C
0/1 规划问题,利用二分 + prim求解。
根据0/1问题模型,只需要构建一张新的无向网,图的结构不变,但每条边只有一个权值 \(C_e - mid * R_e\) ,在新的无向图中求解最大生成树,若最大生成树上边权之和非负,$l = mid $,否则令 \(r = mid\)。
#include<bits/stdc++.h>
using namespace std;
#define dis(a,b) sqrt(pow((nod[a].x - nod[b].x), 2) + pow((nod[a].y - nod[b].y), 2))
const int maxn = 5000;
const int inf = 0x3f3f3f3f;
struct node {
double x, y, c;
}nod[maxn];
int n;
double cost[maxn][maxn];
double a[maxn][maxn];
bool book[maxn];
double d[maxn];
double prim(double mid) {
memset(book, 0, sizeof(book));
for (int i = 1; i <= n; i++)
d[i] = 1e8;
d[1] = 0;
for (int i = 1; i < n; i++) {//一共只需要进行n-1次操作
int x = 0;
for (int j = 1; j <= n; j++)
if (!book[j] && (x == 0 || d[x] > d[j]))//找出没有用过或者距离已选遍最近的点
x = j;
book[x] = true;
for (int y = 1; y <= n; y++)
if (!book[y])d[y] = min(d[y], a[x][y] - mid * cost[x][y]);
}
double ans = 0.0;
for (int i = 2; i <= n; i++) {
ans += d[i];
}
return ans;
}
int main() {
//freopen("in.txt", "r", stdin);
//ios::sync_with_stdio(false), cin.tie(0);
while (scanf("%d", &n), n) {
for (int i = 1; i <= n; i++)
scanf("%lf%lf%lf", &nod[i].x, &nod[i].y, &nod[i].c);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
cost[i][j] = dis(i, j);
a[i][j] = fabs(nod[i].c - nod[j].c);
}
double r = inf, l = 0;
while (r - l > 0.000001) {
double mid = (l + r) / 2;
double ans = prim(mid);
if (ans == 0)
break;
else if (ans > 0)
l = mid;
else
r = mid;
}
printf("%.3lf\n", (r + l) / 2);
}
}
D题:黑暗城堡 (最短路径生成树)
先跑一次dijkstra
对于构造一个树的过程,每个节点都会选择一个节点插入树中
只需要统计每个点能够选择哪些点(满足到1号点距离最小)去插入即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int e[maxn][maxn],inf=1e9;
int dis[maxn],vis[maxn];
const int mod=(1LL<<31)-1;
struct node
{
int s,id;
bool operator < (const node& b) const{
return (this->s)<b.s;
}
}q[maxn];
int main()
{
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++)
e[i][j]=e[j][i]=inf;
}
for(int i=1;i<=m;i++){
int t1,t2,t3;
scanf("%d%d%d",&t1,&t2,&t3);e[t1][t2]=e[t2][t1]=t3;
}
for(int i=1;i<=n;i++) dis[i]=inf;
dis[1]=0;
for(int i=1;i<n;i++){
int u,mx=1e9;
for(int j=1;j<=n;j++){
if(vis[j]) continue;
if(dis[j]<mx){
u=j;mx=dis[j];
}
}
vis[u]=1;
for(int j=1;j<=n;j++){
if(dis[j]>dis[u]+e[u][j]){
dis[j]=dis[u]+e[u][j];
}
}
}
for(int i=1;i<=n;i++){
q[i].s=dis[i];q[i].id=i;
}
sort(q+1,q+1+n);int ans=1;
for(int i=2;i<=n;i++){
int cnt=0;
for(int j=1;j<=n;j++){
if(j==i) continue;
if(dis[i]==dis[j]+e[j][i]) cnt++;
}
//cout<<i<<" "<<cnt<<endl;
ans=1LL*ans*cnt%mod;
}
cout<<ans<<endl;
}