根据题意:
给你边数,和坐标,然后让你输出对应多边形的面积。
思路:先由坐标求三角形,然后多个三角形组合成多边形。
数学原理:
利用了已知三角形的三个顶点的坐标求面积的方法。
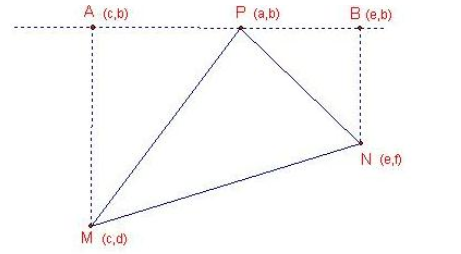
已知直角坐标系3点p(a,b),m(c,d),n(e,f) 求(三角形pmn)面积的表达式!
无论三角形的顶点位置如何,△PMN总可以用一个直角梯形(或矩形)和两个直角三角形面积的和差来表示
而在直角坐标系中,已知直角梯形和直角三角形的顶点的坐标,其面积是比较好求的。
下面以一种情形来说明这个方法,其它情形方法一样,表达式也一样(表达式最好加上绝对值,确保是正值)
如图情形(P在上方,M在左下,N在右下),过P作X轴的平行线L,作MA⊥L,NB⊥L(设P在A、B之间)
则A、B的坐标是A(c,b),B(e,b)
所以(PA=a-c,PB=e-a,AM=b-d,BN=b-f,AB=e-c)
所以
S△PMN=S梯形AMNB-S△PAM-S△PBN
=(b-d+b-f)(e-c)/2-(b-d)(a-c)/2-(b-f)(e-a)/2
=(ad+be+cf-af-bc-de)/2
即:
三角形三顶点坐标分别为(A(a,b),B(c,d),C(e,f)),那么这个三角形的面积为
(S=1/2*三阶行列式),
三阶行列式为:
a b 1
c d 1
e f 1
多变形面积=(n[边数]-2)个三角形面积;
(a*d+c*f+b*e-e*d-c*b-a*f)
注:这里的a与b恒为x[0],y[0]
#include<bits/stdc++.h>
using namespace std;
double x[100], y[100];
float func(int a, int b, int c, int d, int e, int f) {
return (a*d + c * f + e * b - e * d - a * f - b * c) / 2.0;
}
int main() {
ios::sync_with_stdio(false);
int n;
while (cin >> n && n) {
for (int i = 0; i < n; ++i) {
cin >> x[i] >> y[i];
}
float ans = 0;
for (int i = 0; i < n - 2; ++i) {
ans += func(x[0], y[0], x[i + 1], y[i + 1], x[i + 2], y[i + 2]);
}
printf("%.1f
", ans);
}
return 0;
}