一、单项选择题(共20题,每题1.5分,共计30分,每题有且仅有一个正确选项。)
1、 在二进制下,1011001+( )=1100110。
A、1011 B、1101 C、1010 D、1111
B
送分的进制题=w=
2、字符“A”的ASCII码为十六进制41,则字符“Z”的ASCII码为十六进制的()。
A、66 B、5A C、50 D、视具体的计算机而定
B
‘A’十进制为65,‘Z’十进制为90(注意有26个字母不是24个=w=);进制转换
3、右图是一棵二叉树,它的先序遍历是( )。
A、ABDEFC B、DBEFAC C、DFEBCA D、ABCDEF
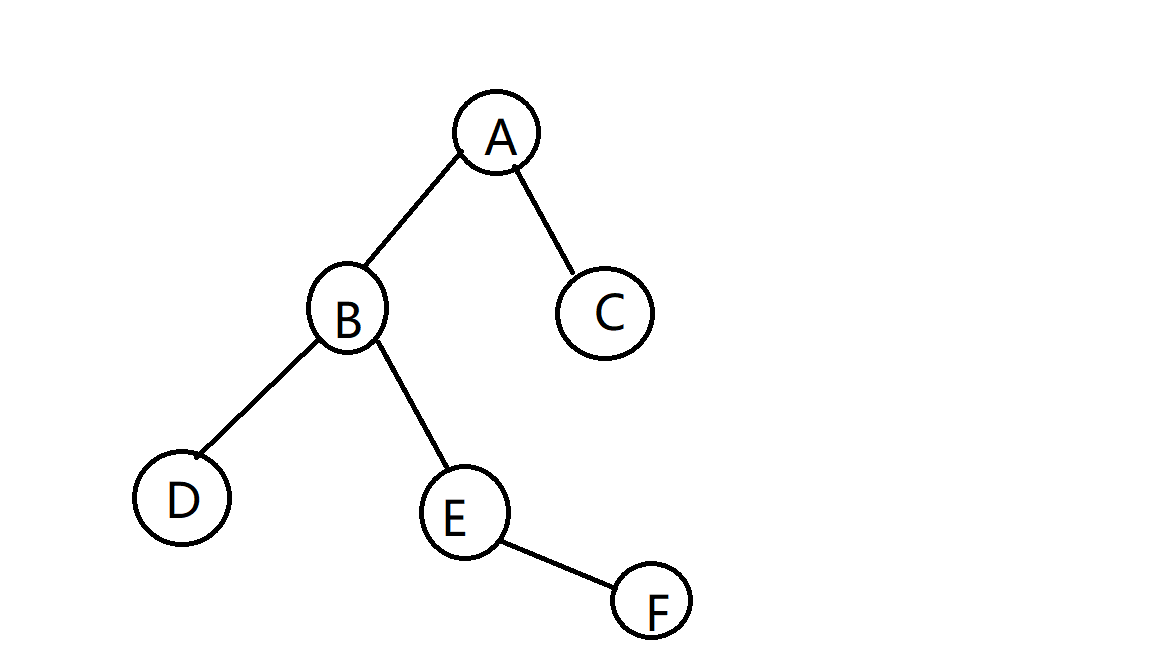
A
先序遍历:根左右
4、寄存器是( )的重要组成部分。
A、硬盘 B、高速缓存 C、内存 D、中央处理器(CPU)
D
寄存器是中央处理器内的组成部分,是CPU内部用来存放数据的一些小型存储区域,用来暂时存放参与运算的数据和运算结果。
5、广度优先搜索时,需要用到的数据结构是( )
A.链表 B.队列 C.栈 D.散列表
B
学过bfs的人都知道=w=
6.在使用高级语言编写程序时,一般提到的“空间复杂度”中的空间是指( )。
A.程序运行时理论上所占的内存空间 B.程序运行时理论上所占的数组空间
C.程序运行时理论上所占的硬盘空间 D.程序源文件理论上所占的硬盘空间
A
首先空间复杂度是运行时的理论值,所占用的存储空间,一般当然指的是内存啦
7.应用快速排序的分治思想,可以实现一个求第K大数的程序。假定不考虑极端的最坏情况,理论上可以实现的最低的算法时间复杂度为( )。
A.$ O (n^2) $ B.$ O (n log n) $ C.$ O (n) $ D. $ O (1) $
C
想了解详情的可以借鉴: http://www.cnblogs.com/pugang/archive/2012/07/02/2573075.html
一般记住就好:极端 ((n^2)) ,一般 $(nlogn) $ ,理论最少 $(n) $。
8.为解决web应用中的不兼容问题,保障信息的顺利流通,( )制定了一系列标准,涉及HTML、XML、CSS等,并建议开发者遵循。
A.微软 B.美国计算机协会(ACM) C.联合国教科文组织 D.万维网联盟(W3C)
D
我觉得就是蒙也会蒙D=w=
万维网联盟(World Wide Web Consortium,W3C)是Web技术领域最具权威和影响力的国际中立性技术标准机构,创建于1994年10月,原为欧洲核子研究组织的一个项目。万维网联盟是国际最著名的标准化组织,主要工作是发展Web规范。它已发布200多项影响深远的Web技术标准及实施指南,如广为业界采用的超文本标记语言(标准通用标记语言下的一个应用)、可扩展标记语言(标准通用标记语言下的一个子集)以及帮助残障人士有效获得Web内容的信息无障碍指南(WCAG)等 ——来自搜狗百科
9.体育课的铃声响了,同学们都陆续的奔向操场,按老师的要求从高到低站成一排。每个同学按顺序来到操场时,都从排尾走到排头,找到第一个比自己高的同学,并站在他的后面。这种站队的方法类似于( )算法。
A.快速排序 B.插入排序 C.冒泡排序 D.归并排序
B
送分题不要,怪我喽=。=
10.1956年( )授予肖克利(William Shockley)、巴丁(John Bardeen)和布拉顿(Walter Brattain)
A.诺贝尔物理学奖 B.约翰•冯•诺依曼奖
C.图灵奖 D.高德纳奖 (Donald E. Knuth Prize)
A
又到了一年一度拼人品的时候了↖(^ω^)↗(如果是我估计第一个就把A排除了=A=)
二、不定项选择题 (共10题,每题1.5分,共计15分。每题正确答案的个数不少于1。多选或少选均不得分)。
1.如果根结点的深度记为1,则一棵恰有2011个叶子结点的二叉树的深度可能是( )。
A.10 B.11 C.12 D.2011
CD
不就是二叉树么,最多一层一个有2011层,每一层节点个数为2^(n-1);显然最少有12层
2.在布尔逻辑中,逻辑“或”的性质有( )。
A.交换律:$ P V Q = Q V P $ B.结合律:$ P V(Q V R)$ = $(PVQ)VR (
C.幂等律:) PVP = P $ D.有界律:$ PV1 = 1 $ (1表示逻辑真)
ABCD
=。=
3.一个正整数在十六进制下有100位,则它在二进制下可能有( )位。
A.399 B.400 C.401 D.404
AB
二进制每四位对应十六进制一位,100位十六进制最多二进制为400位,
4.汇编语言( )。
A.是一种与具体硬件无关的程序设计语言
B.在编写复杂程序时,相对于高级语言而言代码量大,且不易调试
C.可以直接访问寄存器、内存单元、I/O端口
D.随着高级语言的诞生,如今已被完全淘汰,不再使用
BC
显然D是不选的而B是对的,剩下的靠姿势和人品了,姿势正确的话C是显然对的..而汇编语言显然是和硬件有关的...
详情请见各大百科=w=
5.现有一段文言文,要通过二进制哈夫曼编码进行压缩。简单起见,假设这段文言文只由4个汉字“之”、“乎”、“者”、“也”组成,它们出现的次数分别为700、600、300、400。那么,“也”字的编码长度可能是( )。
A.1 B.2 C.3 D.4
BC
到一个集合F中,在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。 从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。本题中,300和400变成一个700的节点,于是700、600、700,于是就会形成两种情况,所以‘也 ’编码长度可能是3或2
6.生物特征识别,是利用人体本身的生物特征进行身份认证的一种技术。目前,指纹识别、虹膜识别、人脸识别等技术已广泛应用于政府、银行、安全防卫等领域。以下属于生物特征识别技术及其应用的是( )。
A.指静脉验证 B.步态验证 C.ATM机密码验证 D.声音验证
ABD
很好蒙,so easy?
7.对于序列“7、5、1、9、3、6、8、4”,在不改变顺序的情况下,去掉( )会使逆序对的个数减少3。
A.7 B.5 C.3 D.6
CD
只要注意前后都考虑就应该没问题了
8.计算机中的数值信息分为整数和实数(浮点数)。实数之所以能够表示很大或者很小的数,是由于使用了( )。
A.阶码 B.补码 C.反码 D.较长的尾数
A
然而我并不会做=。=,百度百科教我
在机器中表示一个浮点数时需要给出指数,这个指数用整数形式表示,这个整数叫做阶码,阶码指明了小数点在数据中的位置。
。浮点数的阶码表示指数大小,有正有负,为避开阶码的符号,对每个阶码都加上一个正的常数(称偏移常数),使能表示的所有阶码都为正整数,变成“偏移”了的阶码,又称“增码”。移码的值不小于0,这样阶码总为0,可以取消,浮点数小数点的实际位置由移码减去偏移常数来决定。
一个任意实数,在计算机内部可以用指数(为整数)和尾数(为纯小数)来表示,用指数和尾数表示实数的方法称为浮点表示法。
浮点数的长度可以是32位、64位甚至更长,分阶码和尾数两部分。阶码位数越多,可表示的数的范围越大;尾数越多,所表示的数的精度越高。——来自百度百科
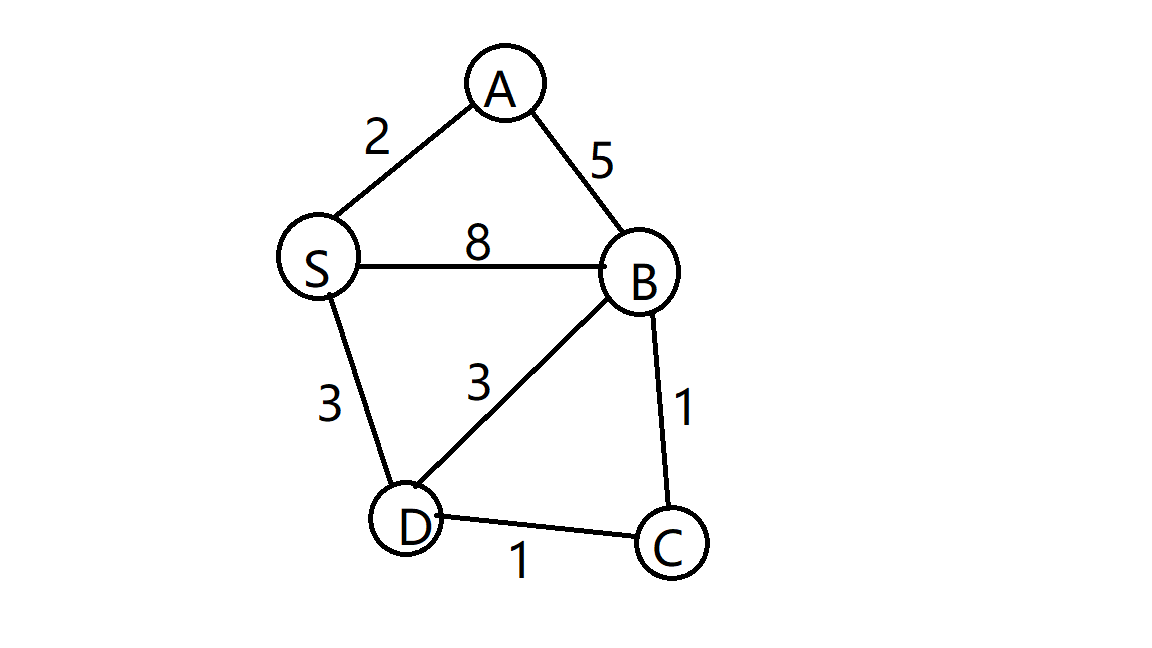
9.对右图使用Dijkstra算法计算S点到其余各点的最短路径长度时,到B点的距离d[B]初始时赋为8,在算法的执行过程中还会出现的值有( )。
A.3 B. 7 C.6 D.5
BCD
10.为计算机网络中进行数据交换而建立的规则、标准或约定的集合称为网络协议。下列英文缩写中,( )是网络协议
A.HTTP B.TCP/IP C.FTP D.WWW
ABC
网络协议为计算机网络中进行数据交换而建立的规则、标准或约定的集合
三个要素描述为:语义表示要做什么,语法表示要怎么做,时序表示做的顺序
Internet上的计算机使用的是TCP/IP协议(TCP/IP(Transmission Control Protocol/Internet Protocol)----传输控制协议/互联网协议是Internet采用的一种标准网络协议。它是由ARPA于1977年到1979年推出的一种网络体系结构和协议规范。随着Internet网的发展,TCP/IP也得到进一步的研究开发和推广应用,成为Internet网上的"通用语言")
三.问题求解(共2题,每空5分,共计10分)
1.平面图可以在画在平面上,且它的边仅在顶点上才能相交的简单无向图。4个顶点的平面图至多有6条边,如右图所示。那么,5个顶点的平面图至多有________条边。
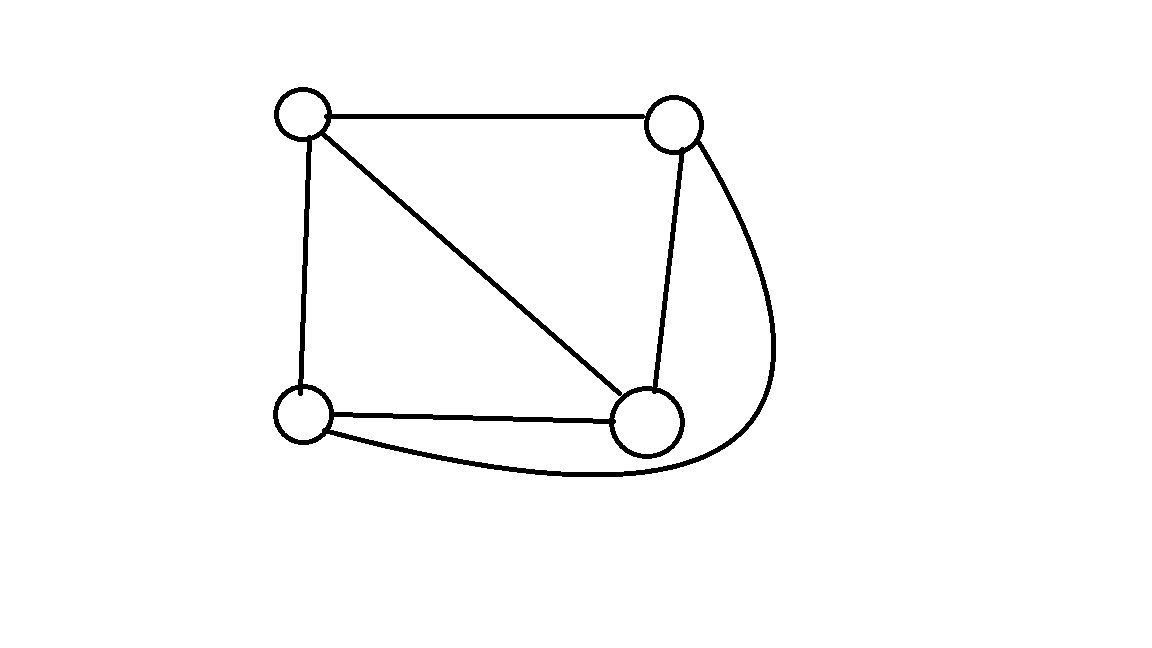
9条,实践出真知=w=
2.定义一种字符串操作,一次可以将其中一个元素移到任意位置。举例说明,对于字符串“BCA”可以将A移到B之前,变字符串“ABC”。如果要将字符串“DACHEBGIF”变成“ABCDEFGHI”最少需要________次操作。
4次
第一次:B放到C前:DABCHEGIF`
第二次:D放到H前:ABCDHEGIF
第三次:F放到G前:ABCDHEFGI
第四次:H放到I前:ABCDEFGHI
四、阅读程序写结果
1、3
2、1 2 5 13 34(隔一个输出一个的Fibonacci)
3、150(这是一个寻找最长路的dfs,走过的点不能再走)
4、57344 (这道题有毒QwQ)
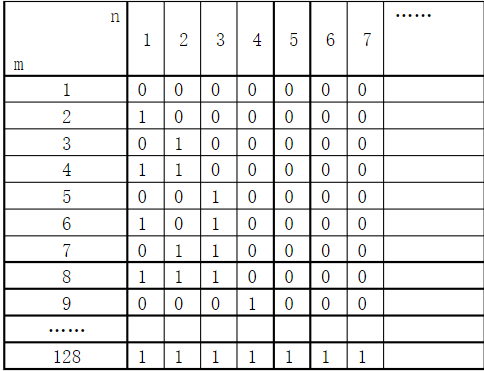
然后我们观察这个m*n的矩阵,可以看出 $ m = 2^n $ , 这个矩阵就是所有的7位2进制数。所以a数组就是0到 $ 2^n-1 $ 的二进制表示。h(i,j)表示第i个数和第j个数有多少位二进制不同,所以答案就是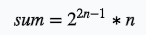 。
。
五
(1)万恶的高精度
1.ans.num[i+j-1]
2.ans.num[i] %= 10
3.a.num[i] + b.num[i]
4.ans.num[i] % 2
5.ans.len++
6.a.len < b.len
7.'0'
8.times(middle , middle) , target
这道题是一高精度运算的大杂烩,加减乘除几乎什么都有。
先看一下这道题的函数,可以知道add是加法,times是乘法。
那么times函数里的(1)和(2)和add函数里的(3)就很明显了,(1)就是不考虑进位的情况下,第i为乘第j位的值,自然(2)就是进位处理。add()函数里的(3)就是对应位相加。
average()是高精度取平均值的操作,其实就是高精度除法,每次除2。读题后发现,ans已经等于a+b,(4)所在的循环正在对ans除以2。然后,然后你就列竖式模拟一下就会发现,(4)是退位操作,就用ans.num[i] % 2就行。
然后看到plustwo操作,就是“加2”,那么(5)就是对长度的修正。
(6)这个空,emmm,不讲了。
然后,主程序里还有两个空,(7)很显然是字符串变数字;那我们看(8),好像整个程序就times一个函数没用过,那就在这里用吧,就是比较middle的平方与target的大小。
(2)神仙笛卡尔树
1.num++
2.j = i
3.solve(left , j - 1 , deep + 1);
4.solve(j + 1 , right , deep + 1);
这是个神仙题,欲知笛卡尔树是个什么东西,我也不知道,请自行百度。
但其实你不知道笛卡尔树是个什么东西并不影响你做这道题。
这个题其实只要你知道中序遍历是什么就能做。
看solve这个函数,就是在left到right这棵树里找这个数的根节点,然后根左根右分别继续solve就行。deep就是深度,maxDeep即使最大深度,所以,如果deep大于maxDeep,maxDeep的值就更新成deep的值。如果deep等于maxDeep,就将最大深度叶节点数num加1,那么(1)就解决了。
而(2),我们先只看if语句,发现这个循环是找当前序列的最小值,再看循环下面的两个if语句,都有j的出现,所以这里应该有一个变量j,记录当前序列的最小值的位置,并当做根,所以(2)应该是j = i;
然后(3)(4)就很明显了,就是向j的左子树和右子树进行分治。根据中序遍历的性质,根的左边是左子树,右边是右子树,分别·进行solve,深度deep+1.