一道睡论数论题
其实是AC300祭才做的水题
题意:
很直白的的题意啊,就是求任意一个多边形的面积
所以我们来安利一下一个求多边形面积的数学通式:
给定多边形的顶点坐标(有序),让你来求这个多边形的面积,你会怎么做?
我们知道,任意多边形都可以分割为N个三角形,所以,如果以这为突破点,那么我们第一步就是把给定的多边形,分割为数个三角形,分别求面积,最后累加就可以了,把多边形分割为三角形的方式多种多样,在这里,我们按照如下图的方法分割:
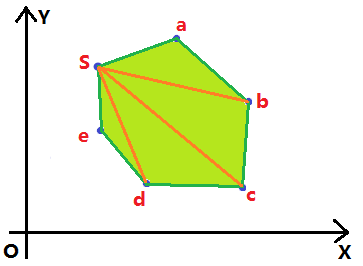
S点作为起始点(点1),a->e依次作为点2,3……。
一个三角形的面积是怎样的呢?
根据线性代数的知识,我们有如下的三角形面积公式,称之为有向面积:
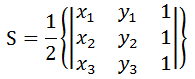
将这个行列式以第三列展开可以得到:
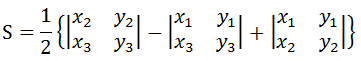
这就是以点1、2、3构成的三角形的有向面积(点如果是顺时针给出,有向面积为负,逆时针给出,有向面积为正),那么继续我们的工作,通过三角形的面积公式,来得到多边形的面积公式:
对于图1而言,多边形的面积就是:
S(1->6)=S(1,2,3)+S(1,3,4)+S(1,4,5)+S(1,5,6)
并且这样做对任意多边形都成立
所以,就有这样的公式:
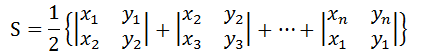
简化得:
$S_Omega = frac{1}{2} sum_{k=1}^{infty} (x_k y_{k + 1} - x_{k + 1} y_k) $
然后就能愉快的水掉这道题了。
CODE:
#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 510
using namespace std;
double x[N],y[N],ans;
int n;
int main() {
scanf("%d",&n);
for(int i = 1 ; i <= n ; i++)
scanf("%lf%lf",&x[i],&y[i]);
x[0] = x[n];
y[0] = y[n];
for(int i = 0 ; i < n ; i++)
ans += 0.5 * (x[i] * y[i + 1] - y[i] * x[i + 1]);
printf("%d
",int(ans) );
return 0;
}