php实现数组中的逆序对（归并排序实现：排序 辅助数组）

php实现数组中的逆序对（归并排序实现：排序 辅助数组）

一、总结

这题用归并排序  线段树   树状数组 等操作的复杂度应该都是小于n方的

二、php实现数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

示例1

输入

1,2,3,4,5,6,7,0

输出

7

三、代码

思路分析：

看到这个题目，我们的第一反应是顺序扫描整个数组。每扫描到一个数组的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成了一个逆序对。假设数组中含有n个数字。由于每个数字都要和O(n)这个数字比较，因此这个算法的时间复杂度为O(n^2)。

我们以数组{7,5,6,4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候，我们不拿ta和后面的每一个数字作比较，否则时间复杂度就是O(n^2)，因此我们可以考虑先比较两个相邻的数字。

 

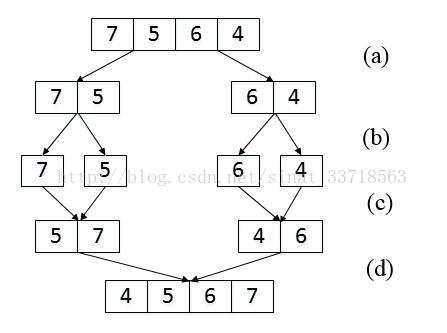
(a) 把长度为4的数组分解成两个长度为2的子数组；

(b) 把长度为2的数组分解成两个成都为1的子数组；

(c) 把长度为1的子数组 合并、排序并统计逆序对 ；

(d) 把长度为2的子数组合并、排序，并统计逆序对；

在上图（a）和（b）中，我们先把数组分解成两个长度为2的子数组，再把这两个子数组分别拆成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7大于5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}、{4}中也有逆序对（6,4）。由于我们已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组 排序 如上图（c）所示， 以免在以后的统计过程中再重复统计。

接下来我们统计两个长度为2的子数组子数组之间的逆序对。合并子数组并统计逆序对的过程如下图如下图所示。

我们先用两个指针分别指向两个子数组的末尾，并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个数组中的数字，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，如下图（a）和（c）所示。如果第一个数组的数字小于或等于第二个数组中的数字，则不构成逆序对，如图b所示。每一次比较的时候，我们都把较大的数字从后面往前复制到一个辅助数组中，确保 辅助数组（记为copy） 中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。

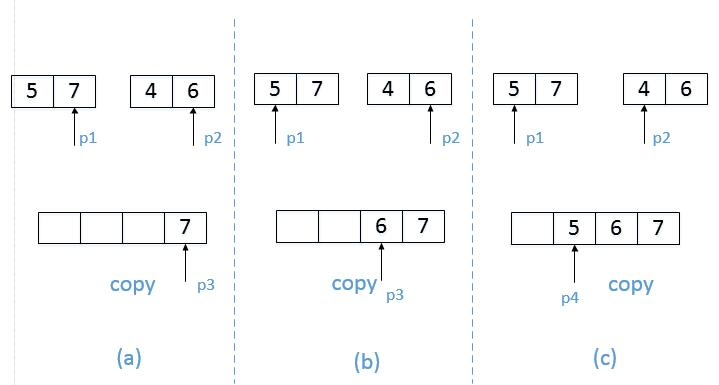
过程：先把数组分割成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序。如果对排序算法很熟悉，我们不难发现这个过程实际上就是归并排序。参考代码如下：

class Solution {
public:
    int InversePairs(vector<int> data) {
       int length=data.size();
        if(length<=0)
            return 0;
       //vector<int> copy=new vector<int>[length];
       vector<int> copy;
       for(int i=0;i<length;i++)
           copy.push_back(data[i]);
       long long count=InversePairsCore(data,copy,0,length-1);
       //delete[]copy;
       return count%1000000007;
    }
    long long InversePairsCore(vector<int> &data,vector<int> &copy,int start,int end)
    {
       if(start==end)
          {
            copy[start]=data[start];
            return 0;
          }
       int length=(end-start)/2;
       long long left=InversePairsCore(copy,data,start,start+length);
       long long right=InversePairsCore(copy,data,start+length+1,end); 
        
       int i=start+length;
       int j=end;
       int indexcopy=end;
       long long count=0;
       while(i>=start&&j>=start+length+1)
          {
             if(data[i]>data[j])
                {
                  copy[indexcopy--]=data[i--];
                  count=count+j-start-length;          //count=count+j-(start+length+1)+1;
                }
             else
                {
                  copy[indexcopy--]=data[j--];
                }          
          }
       for(;i>=start;i--)
           copy[indexcopy--]=data[i];
       for(;j>=start+length+1;j--)
           copy[indexcopy--]=data[j];       
       return left+right+count;
    }
};