P1155 双栈排序(二分图染色)
题目描述
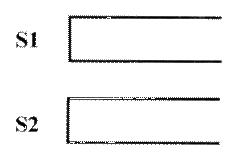
Tom最近在研究一个有趣的排序问题。如图所示,通过2个栈S1和S2,Tom希望借助以下4种操作实现将输入序列升序排序。
操作a
如果输入序列不为空,将第一个元素压入栈S1
操作b
如果栈S1不为空,将S1栈顶元素弹出至输出序列
操作c
如果输入序列不为空,将第一个元素压入栈S2
操作d
如果栈S2不为空,将S2栈顶元素弹出至输出序列
如果一个1~n的排列P可以通过一系列操作使得输出序列为1,2,…,(n-1),n,Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”,而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列:<a,c,c,b,a,d,d,b>
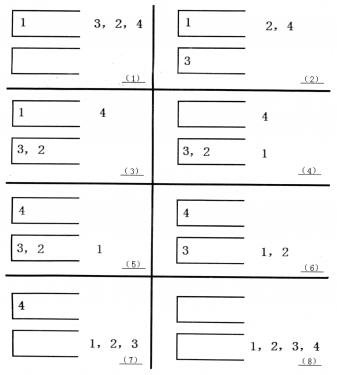
当然,这样的操作序列有可能有几个,对于上例(1,3,2,4),<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。
输入输出格式
输入格式:
输入文件twostack.in的第一行是一个整数n。
第二行有n个用空格隔开的正整数,构成一个1~n的排列。
输出格式:
输出文件twostack.out共一行,如果输入的排列不是“可双栈排序排列”,输出数字0;否则输出字典序最小的操作序列,每两个操作之间用空格隔开,行尾没有空格。
输入输出样例
说明
30%的数据满足: n<=10
50%的数据满足: n<=50
100%的数据满足: n<=1000
题解一:
二分图染色+模拟
1.首先考虑一个简单情况——单栈排序,显然有这样的一个事实:
a[i]和a[j] 不能压入同一个栈⇔存在一个k,使得i < j < k且a[k] < a[i] < a[j]
|
对应变量 |
I |
J |
K |
|
|
下标 |
1 |
2 |
3 |
4 |
|
值a[] |
2 |
3 |
1 |
4 |
显然上面的i,j,k满足关系。
显然上面这个序列不能满足只用一个栈操作这个要求。
时间复杂度为O(n^3).对于n<=1000仍显吃力,对此可以用动态规划的思想,将上述复杂度降到O(n^2)。
状态:f[i]=min(a[i],a[i+1], … ,a[n])
边界条件:f[n+1]=INF;
状态转移方程:f[i]=min(f[i+1],a[i]);
于是上述判断就转化为了f[j+1] < a[i] && a[i] < a[j]
2.扩展到双栈排序:
如果a[i]和a[j]不能在一个栈内,即连接一条i与j之间的无向边,接下来我们只需要判断这个图是否为二分图
由于题目中说编号的字典序要尽可能的小,那么就把编号小的尽可能放到stack1
判断二分图的方法可以采用黑白染色的方式,先从编号小的开始染,第一个顶点染成黑色,相邻的顶点染成不同的颜色,如果发现黑白冲突,那么说明这个图不是一个二分图,是不合法的,输出0.
(DFS或BFS染色均可)
3.染色后所有黑色的点进stack1,所有白色的点进stack2,最后模拟输出过程就可以了.
分析:首先,元素要么用一个栈排序,要么用两个栈排序,如果用一个栈排序,那么字典序可以保证最小,为什么要两个栈呢?因为会存在元素f(i),f(j)不能在一个栈里面排序.什么样的元素不能在同一个栈里面排序呢?当f(i) < f(j) f(i) > f(k),且i < j < k时不行,首先k必须要第一个弹出,因为j > i,在f(k)弹出之前f(i)和f(j)都在栈里面,而f(k)弹出之后f(j) > f(i),而f(j)在栈顶,所以不行.根据这个,我们可以把元素分到两个栈里去排序.可以把两个栈看作一个二分图,可以知道一个栈里面的点不能和栈里另一个点相连,如果满足二分图,那么就可以排序.怎么检测是不是二分图呢?把不能在一个栈里面排序的元素连边,给其中一个元素染色,另一个染不同的颜色,如果一个元素相连的颜色和自己相同则不是二分图.我们在染色的时候把最小的颜色染成最小的.这样在排序的时候就可以满足字典序.然后一个一个扫描,模拟排序即可.
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #define Ll long long 6 using namespace std; 7 int a[1001],v[1001],f[1001]; 8 int q1[1001],top1,q2[1001],top2,now,l; 9 bool ok[1001][1001]; 10 int n; 11 void gg(){printf("0");exit(0);} 12 void dfs(int x,int y) 13 { 14 v[x]=y; 15 for(int i=1;i<=n;i++) 16 if(ok[i][x]) 17 if(v[i]==y)gg();else 18 if(v[i]==0)dfs(i,y^1); 19 } 20 int main() 21 { 22 scanf("%d",&n); 23 for(int i=1;i<=n;i++)scanf("%d",&a[i]); 24 f[n+1]=n+1; 25 for(int i=n;i;i--)f[i]=min(f[i+1],a[i]); 26 for(int i=1;i<=n;i++) 27 for(int j=i+1;j<=n;j++) 28 if(a[i]<a[j]&&a[i]>f[j])ok[i][j]=ok[j][i]=1; 29 for(int i=1;i<=n;i++)if(v[i]==0)dfs(i,2); 30 l=1;now=1;a[0]=n+1; 31 while(now<=n) 32 if(v[l]==2&&a[q1[top1]]>a[l])printf("a "),q1[++top1]=l++;else 33 if(now==a[q1[top1]])printf("b "),top1--,now++;else 34 if(v[l]==3&&a[q2[top2]]>a[l])printf("c "),q2[++top2]=l++;else 35 if(now==a[q2[top2]])printf("d "),top2--,now++; 36 }
可以用贪心或者二分图染色解决
下面讨论贪心的做法
首先我们来讨论单栈排序的性质.
很显然有如下三个性质:
-
栈顶元素一定要大于栈内元素
-
给定序列必须从左至右加入栈, 且只能加入一个栈(只有一个栈)
- 出栈时, 必须最小的先出栈, 然后大的才能出栈
假如我们不考虑当前已经出栈的元素, 根据3条件, 若当前最小值还未入栈, 那么这个栈一定不能弹, 只能一直加, 直到最小值入栈, 那么在这个过程中, 就有可能出现冲突(与1条件冲突). 用公式表达就是 a3 < a1 < a2a3<a1<a2, 如果出现这种情况就说明无解(单栈排序只有进栈和出栈两种选择, 所以没有多种方案).
那么再把单栈排序推广到双栈排序, 唯一的变数就是可以选择加入哪个栈了, 在单栈排序中会GG的 a3 < a1 < a2a3<a1<a2的情况也不会GG了, 考虑为什么不会GG了, 通过思考可以发现, 因为第二个栈可以容纳一个a2a2 所以可以多一条命, 那么如果出现a4 < a1 < a2 < a3a4<a1<a2<a3 的情况, 即使多一个栈也要GG.
不妨设s1s1为主栈, s2s2为辅栈(优先加入s1s1, 因为这样字典序小),
同过题目描述可知, 优先级关系如下:
-
加入s1s1
-
从s1s1弹出
-
加入s2s2
- 从s2s2弹出
我们按照这样的优先级进行每一个操作(即, 如果能加入s1s1就加入s1s1, 否则再考虑能否从s1s1弹出, 否则再考虑加入s2s2...), 弹栈操作无需过多判断, 能弹就弹, 这样一定是最优的, 入栈操作的判断稍微复杂一点, 我们需要判断是否可以把元素加入主栈, 假如当前需要考虑是否加入s1s1的元素为aa, 首先就需要判断它是否满足1条件, 如果满足1条件, 对应到上面的公式, 此时的aa应该是a2a2(为什么不是a1a1?,因为已经入栈的元素的序号一定比未入栈的元素的序号小, a2a2和a1a1刚好满足), 所以我们需要判断它后面是否存在一个a3a3比它大, 并且还有一个a4a4比它小, 如果存在, 那就说明这个元素应该进入辅栈(当然, 如果你发现它连辅栈都进入不了, 那就真的GG了).判断一个元素是否进入辅栈只需要判断这个元素是否满足条件1(比栈顶元素小), 不需要再像主栈那样判断后面是否有.., 为什么? 因为辅栈没有辅栈, 这不是三栈排序!(即使是也不能这么做), 你可能怀疑得这样不会错吗? 当然不会错, 因为我们有最强的1条件守护着辅栈, 在这时就像主栈那样判断.., 反而会错, 因为后面的元素不一定是加入辅栈的, 辅栈只能吃主栈剩下的东西, 假如去判断...,
那么这就是在强制认为这后面的东西是属于辅栈的, 那肯定是不行的!
1 #include <cstdio> 2 #include <cstring> 3 #include <stack> 4 using namespace std; 5 const int N = 1001; 6 const char s[5] = {'r', 'a', 'b', 'c', 'd'}; 7 int data[N], n; 8 stack<int> s1; 9 stack<int> s2; 10 int ans[N * 2], top = 0; 11 int Max[N]; 12 13 bool check(int pos) { 14 if (s2.empty()) return true; 15 int i; 16 for (i = pos + 1; i <= n && (data[i] < data[pos] || data[i] < s2.top()); i++); 17 for (int j = i + 1; j <= n; j++) if (data[j] < data[pos]) return 0; 18 return 1; 19 } 20 21 int main() { 22 // freopen("testdata (7).in", "r", stdin); 23 scanf("%d", &n); 24 for (int i = 1; i <= n; i++) 25 scanf("%d", &data[i]); 26 27 for (int i = n; i >= 1; i--) { 28 Max[i] = max(Max[i + 1], data[i]); 29 } 30 31 bool flag = true; 32 int pos = 1, now = 1; 33 while(pos <= n) { 34 switch(1) { 35 case 1: 36 if ( (s1.empty() || s1.top() > data[pos]) && check(pos)) { 37 s1.push(data[pos]); 38 ans[++top] = 1; 39 pos++; 40 break; 41 } 42 case 2: 43 if (s1.empty() == 0 && s1.top() == now) { 44 ans[++top] = 2; 45 now++; 46 s1.pop(); 47 break; 48 } 49 case 3: 50 if ((s2.empty() || s2.top() > data[pos])) { 51 s2.push(data[pos]); 52 ans[++top] = 3; 53 pos++; 54 break; 55 } 56 case 4: 57 if (s2.empty() == 0 && s2.top() == now) { 58 ans[++top] = 4; 59 now++; 60 s2.pop(); 61 break; 62 } 63 flag = false; 64 } 65 if (flag == false) break; 66 } 67 while ((s1.empty() == 0 || s2.empty() == 0) && flag) { 68 if (s1.empty() == 0 && s1.top() == now) { 69 ans[++top] = 2; 70 now++; 71 s1.pop(); 72 } 73 if (s2.empty() == 0 && s2.top() == now) { 74 ans[++top] = 4; 75 now++; 76 s2.pop(); 77 } 78 } 79 80 if (flag == 0) printf("0 "); 81 else { 82 for (int i = 1; i <= top; i++) { 83 putchar(s[ans[i]]); 84 putchar(' '); 85 } 86 } 87 return 0; 88 }