1623: 街道路径条数

1623: 街道路径条数

时间限制: 1 Sec  内存限制: 128 MB
提交: 111  解决: 21
[提交][状态][讨论版]

题目描述

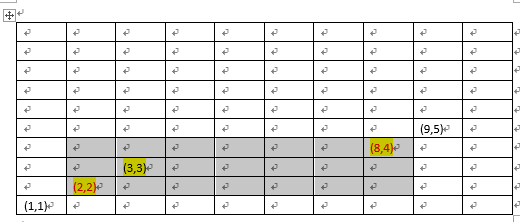
设有一个N*M(l≤N≤50, l≤M≤50)的街道(如下图)：

规定行人从A(1,1)出发,在街道上只能向东或向北方向行 走。如图,从(1,1)点出发,至(3,3)点,共有6条不同的路径： (1,1)-(2,1)-(3,1)-(3,2)-(3,3)； (1,1)-(2,1)-(2,2)-(3,2)-(3,3)； (1,1)-(2,1)-(2,2)-(2,3)-(3,3)；(1,1)-(1,2)-(2,2)-(3,2)-(3,3)； (1,1)-(1,2)-(2,2)-(2,3)-(3,3)； (1,1)-(1,2)-(1,3)-(2,3)-(3,3)；若在N*M的街道中,设置一个矩形障碍区域(包括围住该区域的街道)不让行人通行,如图中用阴影线表示的部分。此矩形障碍区域可以用2对顶点坐标给出,如上图中的障碍区域以2对顶点坐标(2,2),(8,4)表示。此时,从A(1,1)出发至B(9,5),只有两条路径： 路径一：(1,1)-(2,1)-(3,1)-(4,1)-(5,1)-(6,1)-(7,1)-(8,1)-(9,1)-(9,2)-(9,3)-(9,4)-(9,5) 路径二：(1,1)-(1,2)-(1,3)-(1,4)-(1,5)-(2,5)-(3,5)-(4,5)-(5,5)-(6,5)-(7,5)-(8,5)-(9,5) 程序要求：给出N,M,同时再给出此街道中的矩形障碍区域的2对顶点坐标(X1,Y1), (X2,Y2), 然后求出此种情况下所有从(1,1)出发到达(N,M)的路径的条数。

输入

第一行有两个数字,表示N和M； 第二行有两个数字,表示矩形障碍的左下角坐标； 第三行有两个数字,表示矩形障碍的右上角坐标；

输出

只有一个数字,表示求得的路径条数。

样例输入

9 5
2 2
8 4

样例输出

2

提示

 

来源

高精度

分析：

								(9,5)
							(8,4)
		(3,3)
	(2,2)
(1,1)

 

把中间阴影部分置为不可访问。

bool canvis[n][m]={true};

dp[i][j]表示走到(I,j)点的路径条数。

dp[i][j]=max(dp[i][j+1],dp[i+1][j])+1;

if（vis[i][j+1]）{

         dp[i][j]=max(dp[i][j], dp[i][j+1]+1);

}

if（vis[i+1][j]）{

         dp[i][j]=max(dp[i][j], dp[i+1][j]+1);

}