P1629 邮递员送信
题目描述
有一个邮递员要送东西,邮局在节点1.他总共要送N-1样东西,其目的地分别是2~N。由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有M条道路,通过每条道路需要一定的时间。这个邮递员每次只能带一样东西。求送完这N-1样东西并且最终回到邮局最少需要多少时间。
输入输出格式
输入格式:
第一行包括两个整数N和M。
第2到第M+1行,每行三个数字U、V、W,表示从A到B有一条需要W时间的道路。 满足1<=U,V<=N,1<=W<=10000,输入保证任意两点都能互相到达。
【数据规模】
对于30%的数据,有1≤N≤200;
对于100%的数据,有1≤N≤1000,1≤M≤100000。
输出格式:
输出仅一行,包含一个整数,为最少需要的时间。
输入输出样例
5 10 2 3 5 1 5 5 3 5 6 1 2 8 1 3 8 5 3 4 4 1 8 4 5 3 3 5 6 5 4 2
83
Floyed解法40分
1、取边中小的
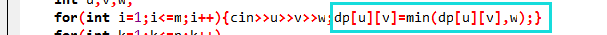
2、ans+=dp[1][i],ans+=dp[i][1]); 显然下面加的方式要好太多

1 #include <bits/stdc++.h> 2 const int N=1e3+10; 3 using namespace std; 4 int dp[N][N],n,m; 5 6 int main(){ 7 //freopen("in.txt","r",stdin); 8 memset(dp,0x3f,sizeof(dp)); 9 cin>>n>>m; 10 int u,v,w; 11 for(int i=1;i<=m;i++){cin>>u>>v>>w;dp[u][v]=min(dp[u][v],w);} 12 for(int k=1;k<=n;k++) 13 for(int i=1;i<=n;i++) 14 for(int j=1;j<=n;j++) 15 dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]); 16 int ans=0; 17 for(int i=2;i<=n;i++) ans+=(dp[1][i]+dp[i][1]); 18 cout<<ans<<endl; 19 return 0; 20 }
这一道题目,是有一些小技巧的。
首先,我们可以看到这样的多源最短路题目,可以先分析一下算法。
Floyd 本题时间复杂度 O ( {n^3} )O(n3)
显然,{1000}^{3}10003=10'0000'0000,肯定会超时(即使在本题可以过4个点,并不止30%)。
Cpp代码:
1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 using namespace std; 5 const int N=1001; 6 const int M=100001; 7 int n,m; 8 int map[N][N]; 9 int min(int x,int y) 10 { 11 return x>y?y:x; 12 } 13 int main() 14 { 15 memset(map,0x3f,sizeof(map)); 16 scanf("%d%d",&n,&m); 17 for(int i=1;i<=m;i++) 18 { 19 int x,y,z; 20 scanf("%d%d%d",&x,&y,&z); 21 map[x][y]=min(map[x][y],z); 22 } 23 for(int k=1;k<=n;k++) 24 for(int i=1;i<=n;i++) 25 for(int j=1;j<=n;j++) 26 map[i][j]=min(map[i][k]+map[k][j],map[i][j]); 27 int ans=0; 28 for(int i=2;i<=n;i++) 29 ans+=(map[i][1]+map[1][i]); 30 printf("%d ",ans); 31 return 0; 32 }
SPFA 本题时间复杂度 O(2kE) 一般k<=2;
怎么做呢?先做一次单源最短路,求出邮局(1)到每个点的距离d_idi。
然后?把所有的边反向存一遍,然后还是求出邮局(1)到每个点的距离d_idi。
为什么这么做正确呢?因为改完之后,我们把t到1的最短路变成1到t的最短路,而路上并不会有任何问题——因为都反向了啊!
相应的,也不会出现更优路线,这个请大家自行思考为什么。
Cpp代码:
1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 const int inf=2147483647; 5 const int maxn=100001; 6 using namespace std; 7 int n,m,s,t,tot=0; 8 int head[maxn],nxt[maxn],d[maxn],vis[maxn],w[maxn],to[maxn]; 9 int x[maxn],y[maxn],z[maxn]; 10 void add(int x,int y,int z) 11 { 12 to[++tot]=y; 13 nxt[tot]=head[x]; 14 head[x]=tot; 15 w[tot]=z; 16 } 17 int spfa(int u,int v) 18 { 19 memset(vis,0,sizeof(vis)); 20 memset(d,0x7f,sizeof(d)); 21 queue<int>q; 22 vis[u]=1;d[u]=0; 23 q.push(u); 24 while(!q.empty()) 25 { 26 int temp=q.front(); 27 vis[temp]=0; 28 q.pop(); 29 for(int i=head[temp];i;i=nxt[i]) 30 { 31 int change=to[i]; 32 if(d[temp]+w[i]<d[change]) 33 { 34 d[change]=d[temp]+w[i]; 35 if(!vis[change]) 36 { 37 vis[change]=1; 38 q.push(change); 39 } 40 } 41 } 42 } 43 int ans=0; 44 for(int i=2;i<=n;i++) 45 ans+=d[i]; 46 return ans; 47 } 48 int main() 49 { 50 scanf("%d%d",&n,&m); 51 for(int i=1;i<=m;i++) 52 { 53 scanf("%d%d%d",&x[i],&y[i],&z[i]); 54 add(x[i],y[i],z[i]); 55 } 56 int ans=spfa(1,n); 57 tot=0; 58 memset(w,0,sizeof(w)); 59 memset(to,0,sizeof(to)); 60 memset(nxt,0,sizeof(nxt)); 61 memset(head,0,sizeof(head)); 62 for(int i=1;i<=m;i++) 63 add(y[i],x[i],z[i]); 64 printf("%d ",ans+spfa(1,n)); 65 return 0; 66 }
Dijkstra 本题时间复杂度 O(2 n{log_2}n2nlog2n)
本题如果用spfa,理论计算量大约是2*2*10'0000=40'0000。
但是如果用Dij,那么计算量将缩小到2*1000*log1000,约等于20000,缩小到了原来的二十分之一。
思路相同,Cpp代码:
1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 using namespace std; 5 const int N=1001; 6 const int M=100001; 7 int n,m,s,t,d[N]; 8 int edge,e[M],b[M],w[M],fir[N]; 9 int x[M],y[M],z[M]; 10 void add(int x,int y,int z) 11 { 12 e[++edge]=y; 13 w[edge]=z; 14 b[edge]=fir[x]; 15 fir[x]=edge; 16 } 17 struct node 18 { 19 int i,dis; 20 }; 21 bool operator<(node a,node b) 22 { 23 return a.dis>b.dis; 24 } 25 priority_queue<node>Q; 26 int main() 27 { 28 scanf("%d%d",&n,&m); 29 for(int i=1;i<=m;i++) 30 { 31 scanf("%d%d%d",&x[i],&y[i],&z[i]); 32 add(x[i],y[i],z[i]); 33 } 34 memset(d,127,sizeof(d)); 35 Q.push((node){1,0}); 36 d[1]=0; 37 while(!Q.empty()) 38 { 39 node t=Q.top(); 40 Q.pop(); 41 if(d[t.i]!=t.dis) 42 continue; 43 for(int k=fir[t.i];k;k=b[k]) 44 { 45 if(t.dis+w[k]<d[e[k]]) 46 { 47 d[e[k]]=t.dis+w[k]; 48 Q.push((node){e[k],d[e[k]]}); 49 } 50 } 51 } 52 int ans=0; 53 for(int i=2;i<=n;i++) 54 ans+=d[i]; 55 edge=0; 56 while(!Q.empty()) Q.pop(); 57 memset(d,127,sizeof(d)); 58 memset(e,0,sizeof(e)); 59 memset(w,0,sizeof(w)); 60 memset(b,0,sizeof(b)); 61 memset(fir,0,sizeof(fir)); 62 for(int i=1;i<=m;i++) 63 add(y[i],x[i],z[i]); 64 Q.push((node){1,0}); 65 d[1]=0; 66 while(!Q.empty()) 67 { 68 node t=Q.top(); 69 Q.pop(); 70 if(d[t.i]!=t.dis) 71 continue; 72 for(int k=fir[t.i];k;k=b[k]) 73 { 74 if(t.dis+w[k]<d[e[k]]) 75 { 76 d[e[k]]=t.dis+w[k]; 77 Q.push((node){e[k],d[e[k]]}); 78 } 79 } 80 } 81 for(int i=2;i<=n;i++) 82 ans+=d[i]; 83 printf("%d ",ans); 84 return 0; 85 }
三种解法各有利弊,
Floyd虽然会超时,但是它也是十分常用的,代码复杂度最低;
spfa是针对稀疏图的,而Dij是针对稠密图的。
希望大家都能够有所了解。