深入理解dijkstra+堆优化
其实就这几种代码几种结构,记住了完全就可以举一反三,所以多记多练多优化多思考。
Dijkstra
最短路满足最优子结构性质,所以是一个动态规划问题。最短路的最优子结构可以描述为:
D(s, t) = {Vs ... Vi ... Vj ... Vt}表示s到t的最短路,其中i和j是这条路径上的两个中间结点,那么D(i, j)必定是i到j的最短路,这个性质是显然的,可以用反证法证明。
基于上面的最优子结构性质,如果存在这样一条最短路D(s, t) = {Vs ... Vi Vt},其中i和t是最短路上相邻的点,那么D(s, i) = {Vs ... Vi} 必定是s到i的最短路。Dijkstra算法就是基于这样一个性质,通过最短路径长度递增,逐渐生成最短路。
Dijkstra算法是最经典的最短路算法,用于计算正权图的单源最短路(Single Source Shortest Path,源点给定,通过该算法可以求出起点到所有点的最短路),它是基于这样一个事实:如果源点到x点的最短路已经求出,并且保存在d[x] ( 可以将它理解为D(s, x) )上,那么可以利用x去更新 x能够直接到达的点 的最短路。即:
d[y] = min{ d[y], d[x] + w(x, y) } y为x能够直接到达的点,w(x, y) 则表示x->y这条有向边的边权
具体算法描述如下:对于图G = <V, E>,源点为s,d[i]表示s到i的最短路,visit[i]表示d[i]是否已经确定(布尔值)。
1) 初始化 所有顶点 d[i] = INF, visit[i] = false,令d[s] = 0;
2) 从所有visit[i]为false的顶点中找到一个d[i]值最小的,令x = i; 如果找不到,算法结束;
3) 标记visit[x] = true, 更新和x直接相邻的所有顶点y的最短路: d[y] = min{ d[y], d[x] + w(x, y) }
(第三步中如果y和x并不是直接相邻,则令w(x, y) = INF)
实例:
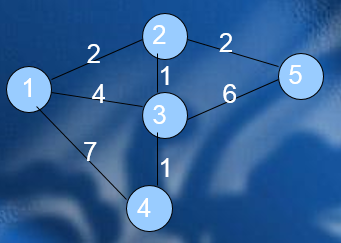
输入:
5 7
1 2 2
2 5 2
1 3 4
1 4 7
3 4 1
2 3 1
3 5 6
1 #include <bits/stdc++.h> 2 using namespace std; 3 int n,m; 4 struct node{ 5 int to; 6 int w; 7 }; 8 int edgeNum[100]; 9 vector<node> vec[100]; 10 int dis[100]; 11 bool vis[100]; 12 13 void addEdge(int a,int b,int w){ 14 edgeNum[a]++; 15 node *p=new node(); 16 p->to=b; 17 p->w=w; 18 vec[a].push_back(*p); 19 } 20 21 void init(){ 22 cin>>n>>m; 23 for(int i=1;i<=m;i++){ 24 int a,b,w; 25 cin>>a>>b>>w; 26 addEdge(a,b,w); 27 addEdge(b,a,w); 28 } 29 } 30 31 void dijkstra(int start){ 32 memset(dis,0x3f,sizeof(dis)); 33 dis[start]=0; 34 for(int i=0;i<edgeNum[start];i++) { 35 int b=vec[start][i].to; 36 int w=vec[start][i].w; 37 dis[b]=w; 38 } 39 vis[start]=1; 40 for(int k=1;k<=n-1;k++){ 41 int minV=0x7fffffff,min_i; 42 for(int i=1;i<=n;i++){ 43 if(!vis[i]&&dis[i]<minV){ 44 minV=dis[i]; 45 min_i=i; 46 } 47 } 48 vis[min_i]=true; 49 for(int i=0;i<edgeNum[min_i];i++){ 50 int b=vec[min_i][i].to; 51 int w=vec[min_i][i].w; 52 if(!vis[b]&&dis[b]>dis[min_i]+w){ 53 dis[b]=dis[min_i]+w; 54 } 55 } 56 57 } 58 59 60 61 } 62 63 void print(){ 64 for(int i=1;i<=n;i++) 65 cout<<dis[i]<<" "; 66 cout<<endl; 67 } 68 69 int main(){ 70 freopen("in.txt","r",stdin); 71 init(); 72 dijkstra(2); 73 print(); 74 return 0; 75 }
上面的代码说几点:
1、13行到19行的代码可以通过给结构体添加构造函数来优化。
2、dijkstra中的节点如果改成u,v的话更清晰
3、朴素的dijkstra分为如下几步:初始化dis数组,n-1轮(找最优节点,更新)
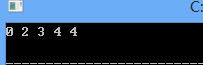
求节点1到其它节点的距离:
堆优化:
1 #include <bits/stdc++.h> 2 using namespace std; 3 int n,m; 4 struct node{ 5 int to; 6 int w; 7 }; 8 int edgeNum[100]; 9 vector<node> vec[100]; 10 int dis[100]; 11 bool vis[100]; 12 13 void addEdge(int a,int b,int w){ 14 edgeNum[a]++; 15 node *p=new node(); 16 p->to=b; 17 p->w=w; 18 vec[a].push_back(*p); 19 } 20 21 void init(){ 22 cin>>n>>m; 23 for(int i=1;i<=m;i++){ 24 int a,b,w; 25 cin>>a>>b>>w; 26 addEdge(a,b,w); 27 addEdge(b,a,w); 28 } 29 } 30 31 void dijkstra(int start){ 32 memset(dis,0x3f,sizeof(dis)); 33 dis[start]=0; 34 for(int i=0;i<edgeNum[start];i++) { 35 int b=vec[start][i].to; 36 int w=vec[start][i].w; 37 dis[b]=w; 38 } 39 vis[start]=1; 40 for(int k=1;k<=n-1;k++){ 41 int minV=0x7fffffff,min_i; 42 for(int i=1;i<=n;i++){ 43 if(!vis[i]&&dis[i]<minV){ 44 minV=dis[i]; 45 min_i=i; 46 } 47 } 48 vis[min_i]=true; 49 for(int i=0;i<edgeNum[min_i];i++){ 50 int b=vec[min_i][i].to; 51 int w=vec[min_i][i].w; 52 if(!vis[b]&&dis[b]>dis[min_i]+w){ 53 dis[b]=dis[min_i]+w; 54 } 55 } 56 57 } 58 } 59 60 61 //dijkstra的堆优化 62 struct qnode{ 63 int i_i; 64 int dis_i; 65 qnode(int i,int dis_i){ 66 this->i_i=i; 67 this->dis_i=dis_i; 68 } 69 }; 70 struct myCmp{ 71 bool operator ()(const qnode &p1,const qnode &p2){ 72 return p1.dis_i>p2.dis_i; 73 } 74 }; 75 priority_queue<qnode,vector<qnode>,myCmp> q; 76 void dijkstra_2(int start){ 77 memset(dis,0x3f,sizeof(dis));//和SPFA一样,这里最开始全都是无穷大 78 dis[start]=0; 79 q.push(qnode(start,dis[start])); 80 while(!q.empty()){ 81 qnode p=q.top(); 82 q.pop(); 83 int min_i= p.i_i; 84 int minV=p.dis_i; 85 if(vis[min_i]) continue; 86 vis[min_i]=true; 87 for(int i=0;i<edgeNum[min_i];i++){ 88 int b=vec[min_i][i].to; 89 int w=vec[min_i][i].w; 90 if(!vis[b]&&dis[b]>dis[min_i]+w){ 91 dis[b]=dis[min_i]+w; 92 q.push(qnode(b,dis[b])); 93 } 94 } 95 96 } 97 } 98 99 void print(){ 100 for(int i=1;i<=n;i++) 101 cout<<dis[i]<<" "; 102 cout<<endl; 103 } 104 105 int main(){ 106 freopen("in.txt","r",stdin); 107 init(); 108 //dijkstra(2); 109 dijkstra_2(1); 110 print(); 111 return 0; 112 }
关于上面的代码说几点:
1、堆优化的话priority_queue得非常熟悉
2、这里堆优化的时候使用了结构体,里面的成员是i和dis[i],其实这个dis[i]可以直接写在外面,但是比较规则还是得自己定义
3、用队列做的所有的题核心代码一定是while(!queue.empty()){}
4、还是要多写多练,要熟悉,基础打好
5、和SPFA一样,如果点更新成功就加进队列
求节点1到其它节点的距离:

堆优化2

1 #include <bits/stdc++.h> 2 using namespace std; 3 int n,m; 4 struct node{ 5 int to; 6 int w; 7 }; 8 int edgeNum[100]; 9 vector<node> vec[100]; 10 int dis[100]; 11 bool vis[100]; 12 13 void addEdge(int a,int b,int w){ 14 edgeNum[a]++; 15 node *p=new node(); 16 p->to=b; 17 p->w=w; 18 vec[a].push_back(*p); 19 } 20 21 void init(){ 22 cin>>n>>m; 23 for(int i=1;i<=m;i++){ 24 int a,b,w; 25 cin>>a>>b>>w; 26 addEdge(a,b,w); 27 addEdge(b,a,w); 28 } 29 } 30 31 void dijkstra(int start){ 32 memset(dis,0x3f,sizeof(dis)); 33 dis[start]=0; 34 for(int i=0;i<edgeNum[start];i++) { 35 int b=vec[start][i].to; 36 int w=vec[start][i].w; 37 dis[b]=w; 38 } 39 vis[start]=1; 40 for(int k=1;k<=n-1;k++){ 41 int minV=0x7fffffff,min_i; 42 for(int i=1;i<=n;i++){ 43 if(!vis[i]&&dis[i]<minV){ 44 minV=dis[i]; 45 min_i=i; 46 } 47 } 48 vis[min_i]=true; 49 for(int i=0;i<edgeNum[min_i];i++){ 50 int b=vec[min_i][i].to; 51 int w=vec[min_i][i].w; 52 if(!vis[b]&&dis[b]>dis[min_i]+w){ 53 dis[b]=dis[min_i]+w; 54 } 55 } 56 57 } 58 } 59 60 61 //dijkstra的堆优化 62 struct myCmp{ 63 bool operator ()(int a,int b){ 64 return dis[a]>dis[b]; 65 } 66 }; 67 priority_queue<int,vector<int>,myCmp> q; 68 void dijkstra_2(int start){ 69 memset(dis,0x3f,sizeof(dis));//和SPFA一样,这里最开始全都是无穷大 70 dis[start]=0; 71 q.push(start); 72 while(!q.empty()){ 73 int u=q.top(); 74 q.pop(); 75 if(vis[u]) continue; 76 vis[u]=true; 77 for(int i=0;i<edgeNum[u];i++){ 78 int b=vec[u][i].to; 79 int w=vec[u][i].w; 80 if(!vis[b]&&dis[b]>dis[u]+w){ 81 dis[b]=dis[u]+w; 82 q.push(b); 83 } 84 } 85 86 } 87 } 88 89 void print(){ 90 for(int i=1;i<=n;i++) 91 cout<<dis[i]<<" "; 92 cout<<endl; 93 } 94 95 int main(){ 96 freopen("in.txt","r",stdin); 97 init(); 98 //dijkstra(2); 99 dijkstra_2(1); 100 print(); 101 return 0; 102 }
关于上面的代码说几点:
1、dijkstra的优先队列优化写法和spfa非常像,只不过spfa多加了一个是否在队列里面的标志
2、这里储存图用的是vector数组
3、优先队列里面的元素是int,然而我们还是重写了优先队列的比较函数,因为队列里面是节点编号,但是我们要比较的是dis[i]
4、和SPFA一样,dis[i]最开始全都是无穷大 ,并且最开始只更新dis[start]=0
求节点1到其它节点的距离:

其它代码:
#include<iostream> #include<cstdio> #include<queue> using namespace std; int n,m,S,tot,Next[500010],head[20000],tree[500010],val[500010]; bool visit[20000]; long long dis[20000]; struct cmp { bool operator()(int a,int b) { return dis[a]>dis[b]; } }; priority_queue<int,vector<int>,cmp> Q; void add(int x,int y,int z) { tot++; Next[tot]=head[x]; head[x]=tot; tree[tot]=y; val[tot]=z; } int main() { scanf("%d%d%d",&n,&m,&S); tot=0; for (int i=1;i<=m;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); if (x==y) continue; add(x,y,z); } for (int i=1;i<=n;i++) { visit[i]=false; dis[i]=2147483647; } Q.push(S); dis[S]=0; while (!Q.empty()) { int u=Q.top(); Q.pop(); if (visit[u]) continue; visit[u]=true; for (int i=head[u];i;i=Next[i]) { int v=tree[i]; if (!visit[v]&&dis[v]>dis[u]+(long long)val[i]) { dis[v]=dis[u]+val[i]; Q.push(v); } } } for (int i=1;i<=n-1;i++) printf("%lld ",dis[i]); printf("%lld ",dis[n]); return 0; }
vector数组版
1 #include <bits/stdc++.h> 2 using namespace std; 3 struct node{ 4 int v; 5 int w; 6 node(int v,int w){ 7 this->v=v; 8 this->w=w; 9 } 10 }; 11 vector<node> vec[100]; 12 int edgeNum[100]; 13 int n,m; 14 int dis[100]; 15 bool vis[100]; 16 17 void addEdge(int u,int v,int w){ 18 edgeNum[u]++; 19 vec[u].push_back(node(v,w)); 20 } 21 22 void init(){ 23 cin>>n>>m; 24 for(int i=1;i<=m;i++){ 25 int u,v,w; 26 cin>>u>>v>>w; 27 addEdge(u,v,w); 28 addEdge(v,u,w); 29 } 30 } 31 32 struct myCmp{ 33 bool operator ()(const int &u,const int &v){ 34 return dis[u]>dis[v]; 35 } 36 }; 37 priority_queue<int,vector<int>,myCmp> q; 38 void dijkstra(int start){ 39 memset(dis,0x3f,sizeof(dis)); 40 q.push(start); 41 dis[start]=0; 42 while(!q.empty()){ 43 int u=q.top(); 44 q.pop(); 45 if(vis[u]) continue; 46 vis[u]=true; 47 for(int i=0;i<edgeNum[u];i++){ 48 int v=vec[u][i].v; 49 int w=vec[u][i].w; 50 if(!vis[v]&&dis[v]>dis[u]+w){ 51 dis[v]=dis[u]+w; 52 q.push(v); 53 } 54 } 55 } 56 } 57 58 void print(){ 59 for(int i=1;i<=n;i++){ 60 cout<<dis[i]<<" "; 61 } 62 cout<<endl; 63 } 64 65 int main(){ 66 freopen("in.txt","r",stdin); 67 init(); 68 dijkstra(2); 69 print(); 70 return 0; 71 }
