P1131 [ZJOI2007]时态同步

P1131 [ZJOI2007]时态同步

题目描述

小Q在电子工艺实习课上学习焊接电路板。一块电路板由若干个元件组成，我们不妨称之为节点，并将其用数字1,2,3….进行标号。电路板的各个节点由若干不相交的导线相连接，且对于电路板的任何两个节点，都存在且仅存在一条通路（通路指连接两个元件的导线序列）。

在电路板上存在一个特殊的元件称为“激发器”。当激发器工作后，产生一个激励电流，通过导线传向每一个它所连接的节点。而中间节点接收到激励电流后，得到信息，并将该激励电流传向与它连接并且尚未接收到激励电流的节点。最终，激烈电流将到达一些“终止节点”――接收激励电流之后不再转发的节点。

激励电流在导线上的传播是需要花费时间的，对于每条边e，激励电流通过它需要的时间为te，而节点接收到激励电流后的转发可以认为是在瞬间完成的。现在这块电路板要求每一个“终止节点”同时得到激励电路――即保持时态同步。由于当前的构造并不符合时态同步的要求，故需要通过改变连接线的构造。目前小Q有一个道具，使用一次该道具，可以使得激励电流通过某条连接导线的时间增加一个单位。请问小Q最少使用多少次道具才可使得所有的“终止节点”时态同步？

输入输出格式

输入格式：

第一行包含一个正整数N，表示电路板中节点的个数。

第二行包含一个整数S，为该电路板的激发器的编号。

接下来N-1行，每行三个整数a , b , t。表示该条导线连接节点a与节点b，且激励电流通过这条导线需要t个单位时间。

输出格式：

仅包含一个整数V，为小Q最少使用的道具次数。

输入输出样例

输入样例#1：

3
1
1 2 1
1 3 3

输出样例#1：

2

说明

对于40%的数据，N ≤ 1000

对于100%的数据，N ≤ 500000

对于所有的数据，te ≤ 1000000

分析：

树形dp

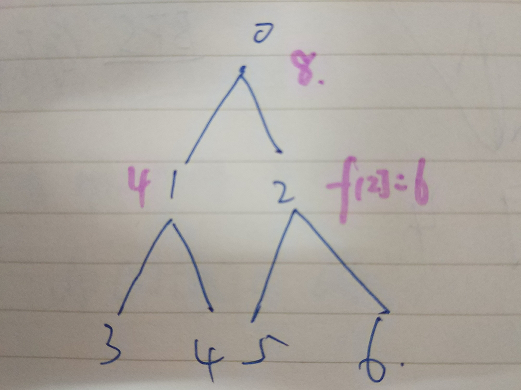
f[i]表示i节点到它的子节点的最远距离。

f[son[i]]表示i的孩子到它（那个孩子）的子节点的最远距离。

c[i]是i节点和子节点边的权值

比如我们看节点2，f[2]=6,f[6]=0,c[2,6]=6,所以节点2到节点6的延迟为0.

f[2]-f[6]-c[2,6]=6-0-6=0;

比如我们看节点0，f[0]=8,f[2]=6,c[0,2]=2,所以节点0到节点2的延迟为0.

f[0]-f[2]-c[0,2]=8-6-2=0;

进行一波dfs，用f[i]记录第i个节点到达最远叶子节点的用时(用时最长的叶子节点).
从每个儿子v回溯回来时，如果从v下去到达最远叶子节点用时更长，那就更新f[u]，f[u]=max(f[u],f[v]+e[i].w)，e[i].w是从u到v的用时。
这样的话遍历完u的所有儿子，答案就增加sigma( f[u]-f[e[i].to]-f[e[i].w )。
大概就是从叶子开始一层层地把兄弟节点统一了，再向上统一这个节点总共要加多少时间，一层层向父亲汇总，回到根节点就得到了答案

#include<stdio.h>
inline int max(int a,int b)
{
    return a>b?a:b;
}
inline int read()
{
    int x=0;
    char ch=getchar();
    while (ch<'0'||ch>'9') ch=getchar();
    while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x;
}
int n,root;

struct edge{
    int next,to;
    int w;
}e[1000010];
int head[500010]={0},cnt=1;
inline void add(int u,int v,int w)
{
    e[cnt].next=head[u];
    e[cnt].to=v;
    e[cnt].w=w;
    head[u]=cnt++;
}
long long f[500010]={0},ans=0;
void dfs(int u,int fa)
{
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        f[u]=max(f[u],f[v]+e[i].w);
    }
    for(int i=head[u];i;i=e[i].next)
        if(fa!=e[i].to)
            ans+=f[u]-f[e[i].to]-e[i].w;
}

int main()
{
    n=read();root=read();
    for(register int i=1,u,v,w;i<n;i++)
        u=read(),v=read(),w=read(),add(u,v,w),add(v,u,w);
    dfs(root,0);
    printf("%lld",ans);
    return 0;
}