递归5--汉诺塔问题的栈实现

递归5--汉诺塔问题的栈实现

汉诺塔的递归解法：http://www.cnblogs.com/Renyi-Fan/p/6949515.html

一、心得

系统里面的递归就是靠栈来维护的，
区别我们普通栈的是维护递归的那个栈有返回地址
递归每深入一层，栈顶元素加一
递归每退出一层，栈顶元素减一
返回地址是执行完这一层，返回到上一层的地址

就是从栈里面取元素然后操作这个元素，如此循环往复，和队列操作几乎完全一样
然而这里用队列不得行，因为最前面的问题分解的子问题没有放在队列最前面

二、分析

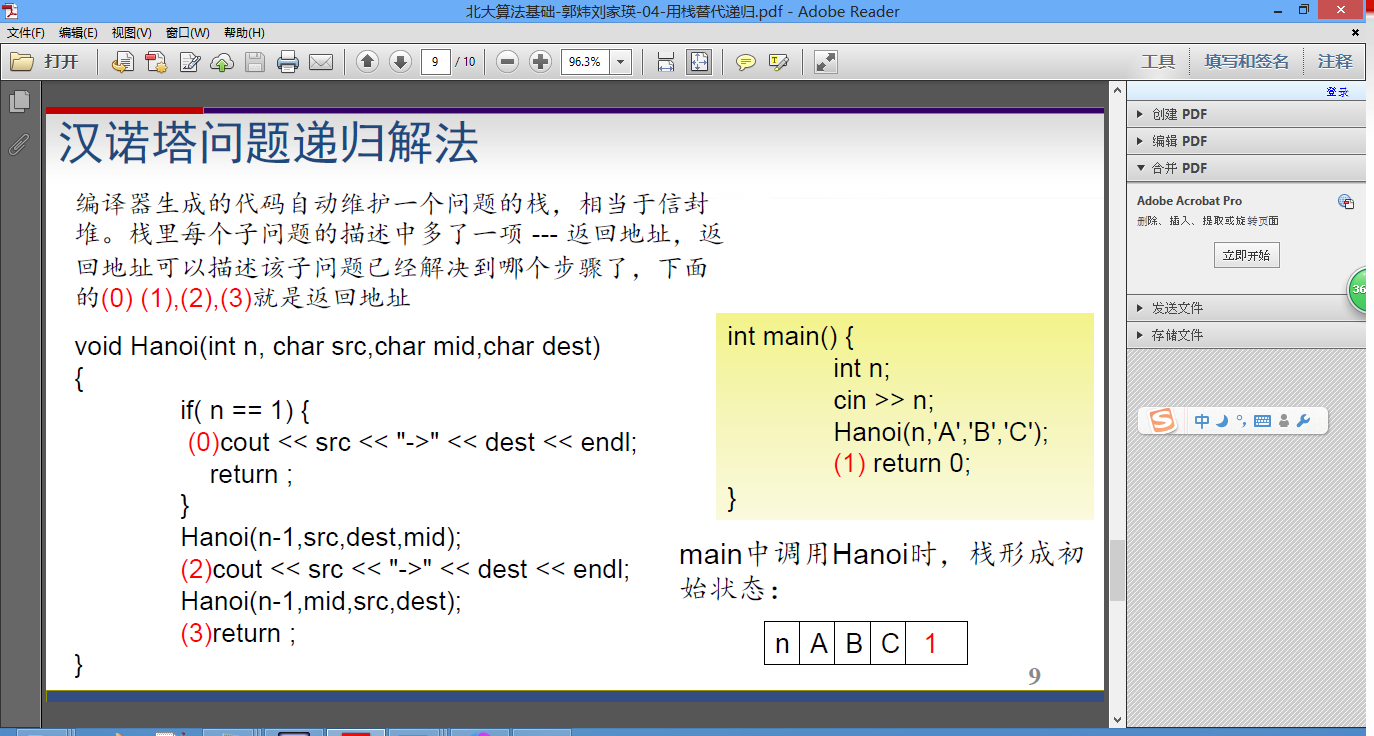
三、代码及结果

/*
汉诺塔问题的栈实现
f(n)=f(n-1)+1+f(n-1)
Problem(n,'A','B','C')=Problem(n-1,'A','C','B')+Problem(1,'A','B','C')+Problem(n,'B','A','C') 
队列不得行，因为最前面的问题分解的子问题没有放在最前面 
*/ 
#include <iostream>
#include <stack>
using namespace std;

struct Problem{
    int n;
    char src,mid,dest;
    Problem(int nn,char s,char m,char d):n(nn),src(s),mid(m),dest(d){
    }
};//一个Problem变量代表一个子问题，将src上的n个盘子
//一mid为中介，移动到dest
stack<Problem> stk;//用来模拟递归的栈，一个元素代表依次操作
//若有n个盘子，则栈的高度不超过n*3，因为出来一个数，进去三个数 
int main(){
    int n;
    cin>>n;
    stk.push(Problem(n,'A','B','C'));//初始化第一轮操作 
    while(!stk.empty()){//只要栈中还有数据，就接着处理 
        Problem curPrb=stk.top();//取最上面的那个子问题，即当前问题
        stk.pop();//因为要对刚刚那个子问题进行操作，所以让子元素直接出栈
        if(curPrb.n==1) cout<<curPrb.src<<"->"<<curPrb.dest<<endl;
        else{
            //分解子问题，子问题要逆序放，因为栈是先进后出 
            //先把分解得到的第三个子问题放入栈中
            stk.push(Problem(curPrb.n-1,curPrb.mid,curPrb.src,curPrb.dest)); 
            //再把第二个子问题放入栈中
            stk.push(Problem(1,curPrb.src,curPrb.mid,curPrb.dest));
            //最后放第一个子问题， 后放入栈的子问题先被处理
            stk.push(Problem(curPrb.n-1,curPrb.src,curPrb.dest,curPrb.mid));
             
        } 
    } 
    return 0;
}