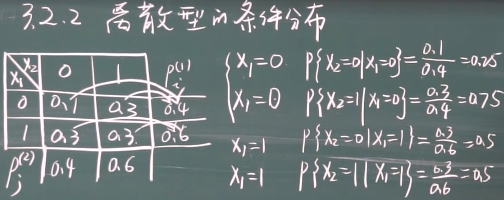宋浩《概率论与数理统计》笔记---查漏补缺
一、总结
一句话总结:
弄完什么东西之后,总结的过程或者说查漏补缺的过程特别特别重要,这样做了之后,那些东西才能真正变成你的
1、随机变量的概念?
【点与数字联系起来】:为了便于描述和解决问题,往往需要对每一个可能的结果指定一个数值,随机变量可以将样本空间中的点与数字联系起来,或者说把事件与数值能联系起来
【数量化的方式表达】:随机变量(random variable)表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。
【用数学分析的方法来研究随机现象】:随机事件数量化的好处是可以用数学分析的方法来研究随机现象。例如某一时间内公共汽车站等车乘客人数,电话交换台在一定时间内收到的呼叫次数,灯泡的寿命等等,都是随机变量的实例。
例:公交车站,每5分钟一辆,候车事件:X表示为[0,5];等车1-3分钟的事件{1<=x<=3},对应概率P{1<=x<=3}
2、二维连续型的边缘分布?
边缘分布用公式特别好求,直接用联合密度函数,X的边缘就对y积分,Y的边缘就对x积分
这个也非常好理解,可以拿离散的边缘分布来说,比如x对应的边缘分布就是把y加起来,而加这个操作在连续型里面就是积分
3、条件分布?
条件分布就是在某条件之下发生的分布,比如某概率密度函数在x>1条件下的分布
比如身高体重,身高限定在1.7,看体重的分布
4、离散型随机变量的条件分布?
就是样本空间发生了改变
5、随机变量函数的数学期望?
就是知道x的期望,此时Y=g(x),求Y的期望
离散性的期望就是xi*pi求和,如果求Y,就是g(x)*pi求和
连续的也是一样,直接把x换成g(x)
6、方差的定义?
图中最下面的公式用的比较多,是根据方差的定义展开来推出来的
7、参数估计-极大似然估计?
概率大的事件比概率小的事件更容易发生
将使A发生的P最大的参数值作为估计值
极大似然估计:就是总体的某些参数未知,通过样本取样来估计这些参数,极大就是最大,似然就是可能性,合起来就是对参数的最大可能性估计
8、大纲前四章?
一、随机事件及其概率
二、随机变量及其分布
三、多维随机变量及其分布
四、随机变量的数字特征(期望、方差、协方差、相关系数等)
9、大纲后三章?
五、大数定理与中心极限定理
六、数理统计的基本概念(比如总体与样本,比如统计量)
七、参数估计(就是来估计参数,比如极大似然估计)
10、概率论总结?
【基本概念】:概率论也就是先讲概率的一些基本知识,然后讲随机变量和一些常用的分布
【一维】:一维的分布将完了,肯定要讲多维的分布的,然后要讲一些期望和方差等数字特征
【一般规律】:然后讲事情的一般规律(也就是大数定理和中心极限定理)
【估计大模型】:最后讲通过少量样本来估计不可取样本(比如人均收入)对应的模型,也就是大模型对应的参数(也就是参数估计)
二、内容在总结中
博客对应课程的视频位置: