TensorFlow优化模型之正则化
一、总结
一句话总结:
一)、正则化:是一种常用的为了避免过度拟合而采用的一种算法。正则化的主要思想是通过在损失函数中加入刻画模型复杂程度的指标,
二)、无论是L1正则化还是L2正则化,两者的目的都是通过限制权重的大小,来使得模型不能任意的拟合训练数据中的随机噪音。
1、l1正则化和l2正则化区别?
①)、L1正则化会让参数变得稀疏,而L2正则化则不会产生这个问题。
②)、参数稀疏是指会有更多的参数变为0,其实就相当于达到了类似于特征选取的功能。
③)、L2正则化不会产生稀疏的原因在于,当参数很小的时候,参数的平方基本上就趋近于0,可以忽略了,而模型不会进一步将这个参数调整为0。
二、TensorFlow优化模型之正则化
转自或参考:TensorFlow优化模型之正则化
https://blog.csdn.net/sinat_29957455/article/details/78397601
在使用机器学习训练一个模型的时候,训练出来的模型很可能会出现两个常见的问题,过拟合和欠拟合从而导致模型对未知数据的预测能力会有所下降。欠拟合可能是由于模型的设计过于的简单,提取出来的特征不足以来刻画问题的趋势,比如说,使用一个模型来预测房价,影响房价的因素有房子所处位置、房子大小、卧室的数量、是否靠近医院、是否靠近学校等等。如果,我们在训练模型的时候仅仅只是用了房子的大小、房子所处的位置两个特征来训练一个预测房价的模型,这就会导致欠拟合的发生,导致模型预测的结果不准确。过拟合指的是,模型对于训练集的拟合程度非常的好,甚至可以达到对于训练数据的损失值为0,而对于未知数据的预测无法做出可靠的判断,原因是因为过拟合使得模型过度拟合训练数据中的噪音而忽视了问题的整体规律。
一、正则化
正则化:是一种常用的为了避免过度拟合而采用的一种算法。正则化的主要思想是通过在损失函数中加入刻画模型复杂程度的指标,假设模型的损失函数为J(θ),那么我们在使用优化算法来优化损失函数的时候,不是直接优化J(θ),而是优化J(θ)+ λ *R(w)。其中R(w)是指模型的复杂程度,λ表示模型复杂损失在总损失中的比例。需要注意的是这里的θ表示的是一个神经网络中的所有参数,它包括权重和偏置。一般来说,模型复杂度只由其权重(w)来决定。而常用的来刻画模型复杂度的函数R(w)有两种,一种是L1正则化,计算公式如下,以下公式中w都是从w1到wn:

还有一种L2正则化,计算公式如下:
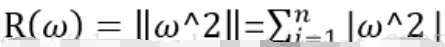
无论是L1正则化还是L2正则化,两者的目的都是通过限制权重的大小,来使得模型不能任意的拟合训练数据中的随机噪音。两者正则化也有很大的区别。L1正则化会让参数变得稀疏,而L2正则化则不会产生这个问题。参数稀疏是指会有更多的参数变为0,其实就相当于达到了类似于特征选取的功能。L2正则化不会产生稀疏的原因在于,当参数很小的时候,参数的平方基本上就趋近于0,可以忽略了,而模型不会进一步将这个参数调整为0。L1正则化的计算公式不可导,L2正则化可导。而在优化模型的时候需要计算损失函数的偏导数,所以对于这种情况L2比较合适。在实践中,也可以将L1正则化和L2正则化同时使用:
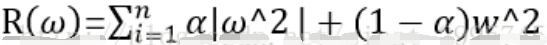
二、TensorFlow中的正则化
在简单的神经网络中,加入正则化来计算损失函数还是比较容易的。当,神经网络变得非常复杂(层数很多)的时候,那么在损失函数中加入正则化的就会变得非常的复杂,使得损失函数的定义变得很长,从而还会导致程序的可读性变差。而且还有可能,当神经网络变得复杂的时候,定义网络结构的部分和计算损失函数的部分不在同一个函数中,这样就会使得计算损失函数不方便。TensorFlow提供了集合的方式,通过在计算图中保存一组实体,来解决这一类问题。
import tensorflow as tf
from numpy.random import RandomState
#获取一层神经网络的权重,并将权重的L2正则化损失加入到集合中
def get_weight(shape,lamda):
#定义变量
var = tf.Variable(tf.random_normal(shape=shape),dtype=tf.float32)
#将变量的L2正则化损失添加到集合中
tf.add_to_collection("losses",tf.contrib.layers.l2_regularizer(lamda)(var))
return var
if __name__=="__main__":
#定义输入节点
x = tf.placeholder(tf.float32,shape=(None,2))
#定义输出节点
y_ = tf.placeholder(tf.float32,shape=(None,1))
#定义每次迭代数据的大小
batch_size = 8
#定义五层神经网络,并设置每一层神经网络的节点数目
layer_dimension = [2,10,10,10,1]
#获取神经网络的层数
n_layers = len(layer_dimension)
#定义神经网络第一层的输入
cur_layer = x
#当前层的节点个数
in_dimension = layer_dimension[0]
#通过循环来生成5层全连接的神经网络结构
for i in range(1,n_layers):
#定义神经网络上一层的输出,下一层的输入
out_dimension = layer_dimension[i]
#定义当前层中权重的变量,并将变量的L2损失添加到计算图的集合中
weight = get_weight([in_dimension,out_dimension],0.001)
#定义偏置项
bias = tf.Variable(tf.constant(0.1,shape=[out_dimension]))
#使用RELU激活函数
cur_layer = tf.nn.relu(tf.matmul(cur_layer,weight) + bias)
#定义下一层神经网络的输入节点数
in_dimension = layer_dimension[i]
#定义均方差的损失函数
mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
#将均方差孙函数添加到集合
tf.add_to_collection("losses",mse_loss)
#获取整个模型的损失函数,tf.get_collection("losses")返回集合中定义的损失
#将整个集合中的损失相加得到整个模型的损失函数
loss = tf.add_n(tf.get_collection("losses"))