KL散度、JS散度、Wasserstein距离
一、总结
一句话总结:
①)、KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布P和Q 差别的非对称性的度量。
②)、JS散度度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。
③)、Wessertein距离相比KL散度和JS散度的优势在于即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。
1、KL散度?
I)、KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布P和Q 差别的非对称性的度量。
II)、KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。
III)、典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
IV)、定义:$$D _ { K L } ( P / / Q ) = - sum _ { x in X } P ( x ) log frac { 1 } { P ( x ) } + sum _ { x in X } P ( x ) log frac { 1 } { Q ( x ) }$$
2、KL散度的值为非负数?
因为对数函数是凸函数,所以KL散度的值为非负数。
3、有时会将KL散度称为KL距离,但它并不满足距离的性质?
1、KL散度不是对称的:KL(A,B)≠KL(B,A)
2、KL散度不满足三角不等式: KL(A,B)>KL(A,C)+KL(C,B)
4、JS散度(Jensen-Shannon)?
(a)、JS散度度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。
(b)、一般地,JS散度是对称的,其取值是0到1之间。
(c)、js散度定义:$$J S ( p | q ) = frac { 1 } { 2 } K L ( p | frac { p + q } { 2 } ) + frac { 1 } { 2 } K L ( q | frac { p + q } { 2 } )$$
5、KL散度和JS散度度量的时候有一个问题?
如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
6、Wessertein距离相比KL散度和JS散度的优势在于?
即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。
二、KL散度、JS散度、Wasserstein距离
转自或参考:KL散度、JS散度、Wasserstein距离
https://blog.csdn.net/leviopku/article/details/81388306
1. KL散度
KL散度又称为相对熵,信息散度,信息增益。KL散度是是两个概率分布P和Q 差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
定义如下:
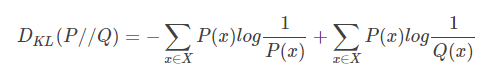
因为对数函数是凸函数,所以KL散度的值为非负数。
有时会将KL散度称为KL距离,但它并不满足距离的性质:
1. KL散度不是对称的:KL(A,B)≠≠KL(B,A)
2. KL散度不满足三角不等式: KL(A,B)>>KL(A,C)+KL(C,B)
2. JS散度(Jensen-Shannon)
JS散度度量了两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。一般地,JS散度是对称的,其取值是0到1之间。定义如下: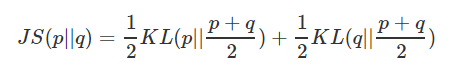
KLKL散度和JSJS散度度量的时候有一个问题:
如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
3. Wasserstein距离
WassersteinWasserstein距离度量两个概率分布之间的距离,定义如下:
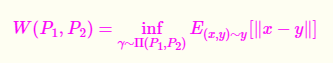

Wessertein距离相比KL散度和JS散度的优势在于:
即使两个分布的支撑集没有重叠或者重叠非常少,仍然能反映两个分布的远近。而JS散度在此情况下是常量,KL散度可能无意义。