200812_深度学习系列---2、线性单元和梯度下降
一、总结
一句话总结:
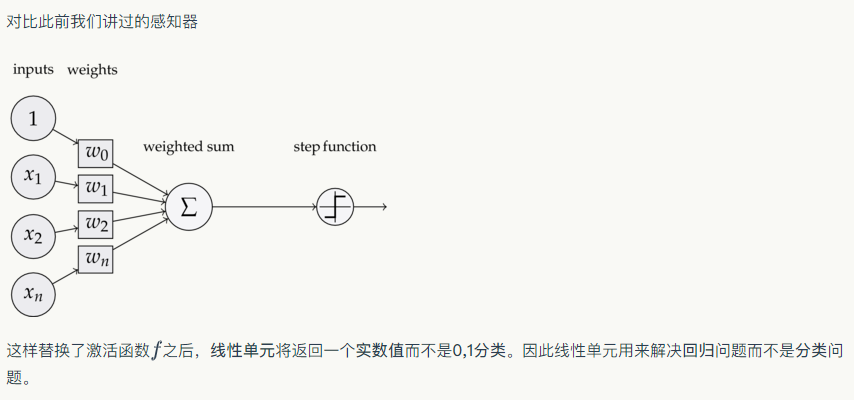
线性单元感知器,知识激活函数变了,其它代码都一样
from perceptron import Perceptron #定义激活函数f f = lambda x: x class LinearUnit(Perceptron): def __init__(self, input_num): '''初始化线性单元,设置输入参数的个数''' Perceptron.__init__(self, input_num, f)
1、训练样本的y叫label?
每个训练样本既包括输入特征x,也包括对应的输出y(y也叫做标记,label)。
2、损失函数为什么也叫目标函数?
因为损失函数E(x)就是我们要优化的目标,所以叫目标函数
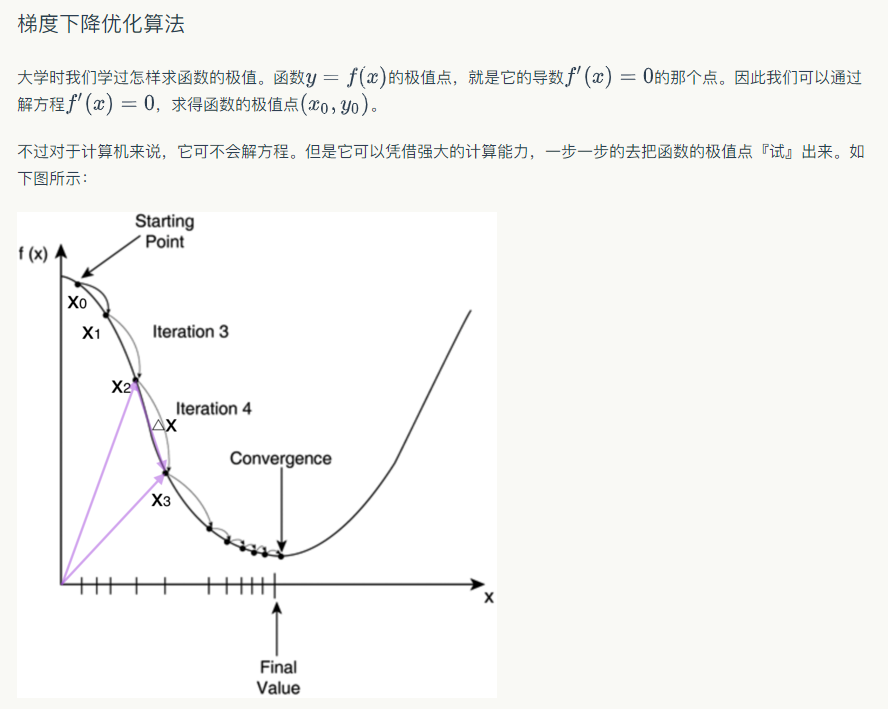
3、梯度下降算法(梯度下降算法也就这样一个简简单单的式子,当然反向传播也很简单)?
$$x _ { n e w } = x _ { o l d } - eta abla f ( x )$$
4、目标函数梯度:$$E ( w ) = frac { 1 } { 2 } sum _ { i = 1 } ^ { n } ( y ^ { ( i ) } - overline { y } ^ { ( i ) } ) ^ { 2 }$$?
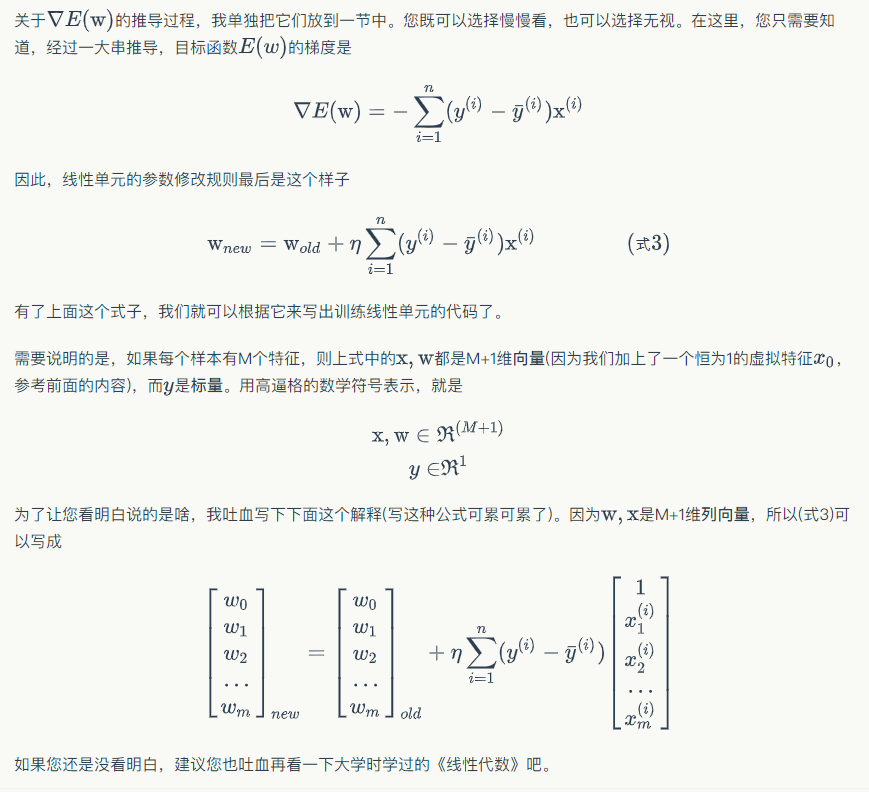
A、求E(w)梯度:$$ abla E ( w ) = - sum _ { i = 1 } ^ { n } ( y ^ { ( i ) } - overline { y } ^ { ( i ) } ) x ^ { ( i ) }$$
B、对应梯度公式:$$w _ { n e w } = w _ { o l d } + eta sum _ { i = 1 } ^ { n } ( y ^ { ( i ) } - overline { y } ^ { ( i ) } ) x ^ { ( i ) }$$
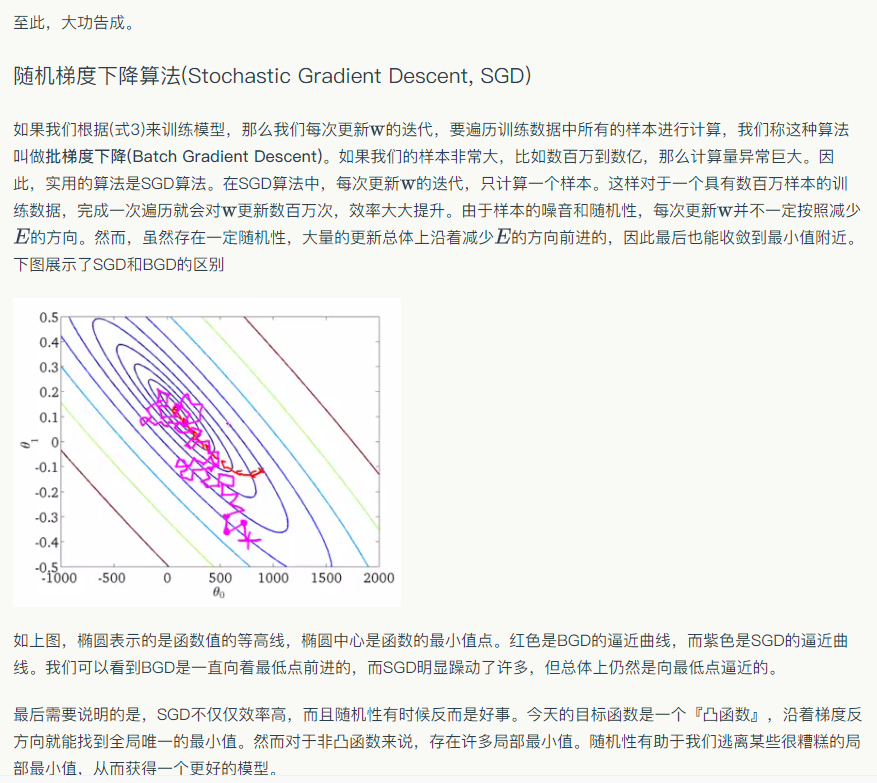
5、随机梯度下降算法(Stochastic Gradient Descent, SGD)?
I、如果我们根据w'=w-lr*(∂(loss)/∂(w))来训练模型,那么我们每次更新w的迭代,要遍历训练数据中所有的样本进行计算,我们称这种算法叫做批梯度下降(Batch Gradient Descent)。
II、如果我们的样本非常大,比如数百万到数亿,那么计算量异常巨大。因此,实用的算法是SGD算法。
III、在SGD算法中,每次更新w的迭代,只计算一个样本。这样对于一个具有数百万样本的训练数据,完成一次遍历就会对w更新数百万次,效率大大提升。
IV、由于样本的噪音和随机性,每次更新w并不一定按照减少E的方向。然而,虽然存在一定随机性,大量的更新总体上沿着减少E的方向前进的,因此最后也能收敛到最小值附近。
6、随机梯度下降算法(Stochastic Gradient Descent, SGD)的好处?
一、SGD不仅仅效率高,而且随机性有时候反而是好事。今天的目标函数是一个『凸函数』,沿着梯度反方向就能找到全局唯一的最小值。
二、然而对于非凸函数来说,存在许多局部最小值。随机性有助于我们逃离某些很糟糕的局部最小值,从而获得一个更好的模型。
二、线性单元和梯度下降
转自或参考:零基础入门深度学习(2) - 线性单元和梯度下降
https://www.zybuluo.com/hanbingtao/note/448086









rom perceptron import Perceptron #定义激活函数f f = lambda x: x class LinearUnit(Perceptron): def __init__(self, input_num): '''初始化线性单元,设置输入参数的个数''' Perceptron.__init__(self, input_num, f)
通过继承Perceptron,我们仅用几行代码就实现了线性单元。这再次证明了面向对象编程范式的强大。
接下来,我们用简单的数据进行一下测试。
def get_training_dataset(): ''' 捏造5个人的收入数据 ''' # 构建训练数据 # 输入向量列表,每一项是工作年限 input_vecs = [[5], [3], [8], [1.4], [10.1]] # 期望的输出列表,月薪,注意要与输入一一对应 labels = [5500, 2300, 7600, 1800, 11400] return input_vecs, labels def train_linear_unit(): ''' 使用数据训练线性单元 ''' # 创建感知器,输入参数的特征数为1(工作年限) lu = LinearUnit(1) # 训练,迭代10轮, 学习速率为0.01 input_vecs, labels = get_training_dataset() lu.train(input_vecs, labels, 10, 0.01) #返回训练好的线性单元 return lu if __name__ == '__main__': '''训练线性单元''' linear_unit = train_linear_unit() # 打印训练获得的权重 print linear_unit # 测试 print 'Work 3.4 years, monthly salary = %.2f' % linear_unit.predict([3.4]) print 'Work 15 years, monthly salary = %.2f' % linear_unit.predict([15]) print 'Work 1.5 years, monthly salary = %.2f' % linear_unit.predict([1.5]) print 'Work 6.3 years, monthly salary = %.2f' % linear_unit.predict([6.3])
程序运行结果如下图
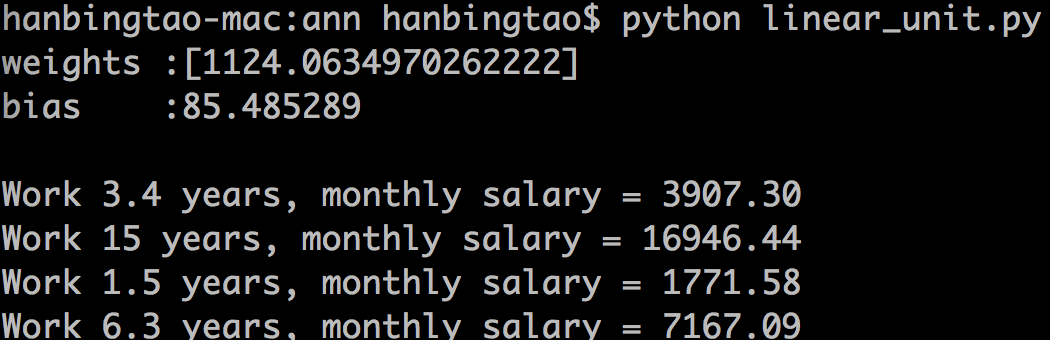
拟合的直线如下图
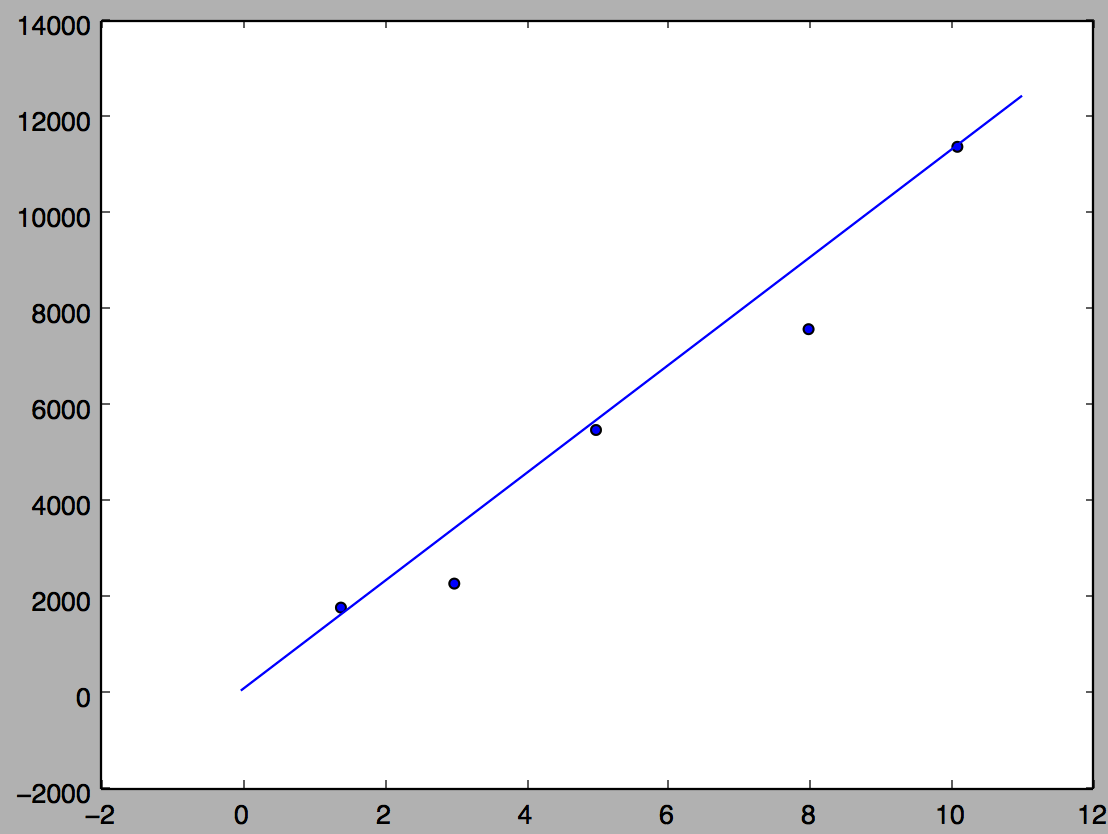
#!/usr/bin/env python # -*- coding: UTF-8 -*- from perceptron import Perceptron #定义激活函数f f = lambda x: x class LinearUnit(Perceptron): def __init__(self, input_num): '''初始化线性单元,设置输入参数的个数''' Perceptron.__init__(self, input_num, f) def get_training_dataset(): ''' 捏造5个人的收入数据 ''' # 构建训练数据 # 输入向量列表,每一项是工作年限 input_vecs = [[5], [3], [8], [1.4], [10.1]] # 期望的输出列表,月薪,注意要与输入一一对应 labels = [5500, 2300, 7600, 1800, 11400] return input_vecs, labels def train_linear_unit(): ''' 使用数据训练线性单元 ''' # 创建感知器,输入参数的特征数为1(工作年限) lu = LinearUnit(1) # 训练,迭代10轮, 学习速率为0.01 input_vecs, labels = get_training_dataset() lu.train(input_vecs, labels, 10, 0.01) #返回训练好的线性单元 return lu def plot(linear_unit): import matplotlib.pyplot as plt input_vecs, labels = get_training_dataset() fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(map(lambda x: x[0], input_vecs), labels) weights = linear_unit.weights bias = linear_unit.bias x = range(0,12,1) y = map(lambda x:weights[0] * x + bias, x) ax.plot(x, y) plt.show() if __name__ == '__main__': '''训练线性单元''' linear_unit = train_linear_unit() # 打印训练获得的权重 print linear_unit # 测试 print 'Work 3.4 years, monthly salary = %.2f' % linear_unit.predict([3.4]) print 'Work 15 years, monthly salary = %.2f' % linear_unit.predict([15]) print 'Work 1.5 years, monthly salary = %.2f' % linear_unit.predict([1.5]) print 'Work 6.3 years, monthly salary = %.2f' % linear_unit.predict([6.3]) plot(linear_unit)

参考资料
- Tom M. Mitchell, "机器学习", 曾华军等译, 机械工业出版社