梯度消失和梯度爆炸原因及其解决方案
一、总结
一句话总结:
A)、当神经元层数变多时,链式法则求梯度会遇到很多个连乘,连乘多了,如果大了,梯度就爆炸了,如果小了,梯度就消失了
B)、我们知道Sigmoid函数有一个缺点:当x较大或较小时,导数接近0;并且Sigmoid函数导数的最大值是0.25
C)、因此所有的权重通常会满足|wj|<1,而s‘是小于0.25的值,那么当神经网络特别深的时候,梯度呈指数级衰减,导数在每一层至少会被压缩为原来的1/4,当z值绝对值特别大时,导数趋于0,
D)、从输出层不断向输入层反向传播训练时,导数很容易逐渐变为0,使得权重和偏差参数无法被更新,导致神经网络无法被优化,训练永远不会收敛到良好的解决方案。
1、sigmoid梯度消失在生物学误导方面的启示?
生物神经元似乎是用 Sigmoid(S 型)激活函数活动的,因此研究人员在很长一段时间内坚持 Sigmoid 函数。但事实证明,Relu 激活函数通常在一些情况表现的好。这是生物研究误导的例子之一。
2、梯度消失或者梯度爆炸,简单一点来讲就是层数太多,链式求梯度的时候连乘太多?
当然这也不是绝对原因,比如对sigmoid,本身导数最大就0.25,每次至少变小4倍
3、解决梯度消失或者梯度爆炸的常用方法?
(①)、好的参数初始化方式,如He初始化
(②)、非饱和的激活函数(如 ReLU)
(③)、批量规范化(Batch Normalization)
(④)、梯度截断(Gradient Clipping)
二、梯度消失和梯度爆炸原因及其解决方案
转自或参考:梯度消失和梯度爆炸原因及其解决方案
https://blog.csdn.net/junjun150013652/article/details/81274958
当我们需要解决一个非常复杂的问题,例如在高分辨率图像中检测数百种类型的对象,我们可能需要训练一个非常深的DNN,可能需要几十层或者上百层,每层包含数百个神经元,通过成千上万个连接进行连接,我们会遇到以下问题:
首先,梯度消失或梯度爆炸
其次,训练缓慢
第三,训练参数大于训练集的风险
梯度消失的原因:
生物神经元似乎是用 Sigmoid(S 型)激活函数活动的,因此研究人员在很长一段时间内坚持 Sigmoid 函数。但事实证明,Relu 激活函数通常在 ANN 工作得更好。这是生物研究误导的例子之一。
当神经网络有很多层,每个隐藏层都使用Sigmoid函数作为激励函数时,很容易引起梯度消失的问题
我们知道Sigmoid函数有一个缺点:当x较大或较小时,导数接近0;并且Sigmoid函数导数的最大值是0.25

我们将问题简单化来说明梯度消失问题,假设输入只有一个特征,没有偏置单元,每层只有一个神经元:

我们先进行前向传播,这里将Sigmoid激励函数写为s(x):
z1 = w1*x
a1 = s(z1)
z2 = w2*a1
a2 = s(z2)
...
zn = wn*an-1 (这里n-1是下标)
an = s(zn)
根据链式求导和反向传播,我们很容易得出,其中C是代价函数
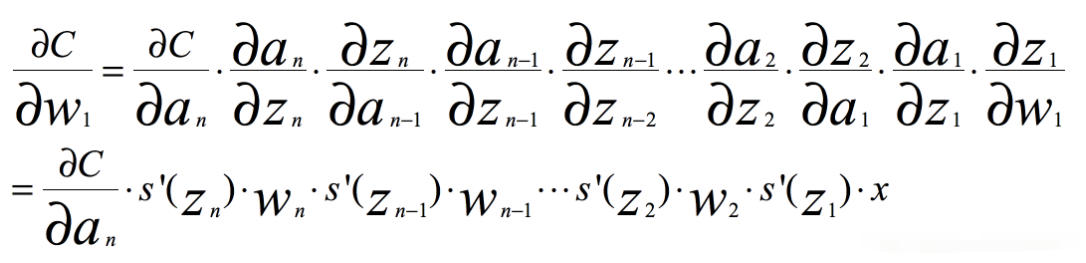
如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足|wj|<1,而s‘是小于0.25的值,那么当神经网络特别深的时候,梯度呈指数级衰减,导数在每一层至少会被压缩为原来的1/4,当z值绝对值特别大时,导数趋于0,正是因为这两个原因,从输出层不断向输入层反向传播训练时,导数很容易逐渐变为0,使得权重和偏差参数无法被更新,导致神经网络无法被优化,训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。
那么我们继续推广到每层有多个神经元时,有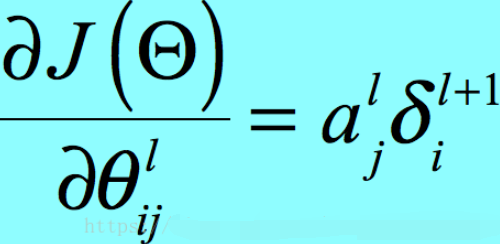
其中a是Sigmoid函数的输出,那么它的范围就是-1<a<1,那么我们只考虑δ,有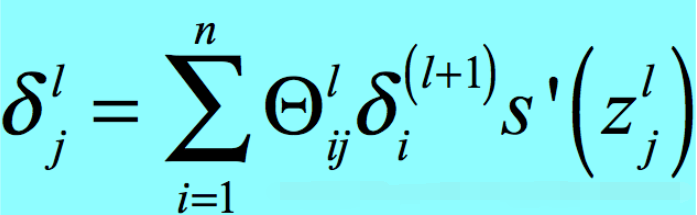
那么很容易得出当参数|θ|<1时,容易引发梯度消失。
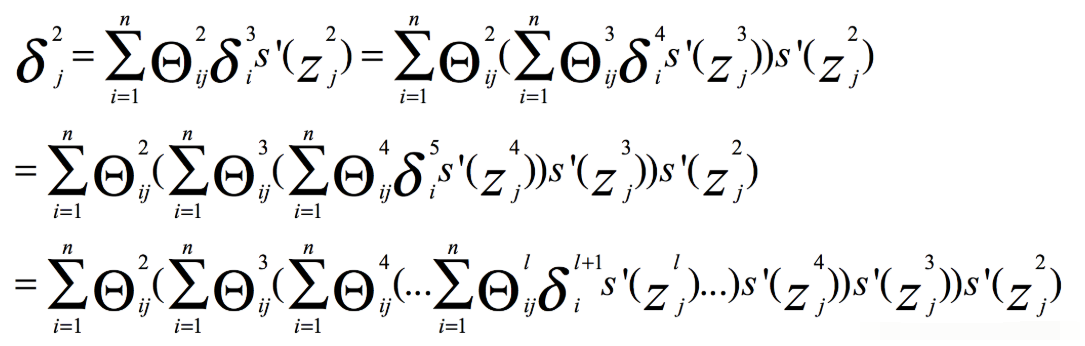
梯度爆炸的原因:
当我们将w初始化为一个较大的值时,例如>10的值,那么从输出层到输入层每一层都会有一个s‘(zn)*wn的增倍,当s‘(zn)为0.25时s‘(zn)*wn>2.5,同梯度消失类似,当神经网络很深时,梯度呈指数级增长,最后到输入时,梯度将会非常大,我们会得到一个非常大的权重更新,这就是梯度爆炸的问题,在循环神经网络中最为常见.
解决方案:
好的参数初始化方式,如He初始化
非饱和的激活函数(如 ReLU)
批量规范化(Batch Normalization)
梯度截断(Gradient Clipping)
更快的优化器
LSTM
参考资料:Hands-On_Machine_Learning_with_Scikit-Learn_and_TensorFlow