秒懂机器学习---梯度下降简单实例
一、总结
一句话总结:
机器学习中:但凡能够把数据映射到多维空间的那个图形上,那么事情就变的比较好解决了
别人要不要你,就是看你有没有震撼到别人,你的各个方面的实力和魅力
1、python支持函数中定义函数实例?
python中函数里面可以定义函数:比如在梯度下降中我们可以把 偏导那个函数定义在梯度下降函数里面
def test(): def derivative(x_pre): # f(x)的导数 return 2 * x_pre + 3
2、梯度下降真的非常简单,最核心理解的是哪两步?
1、将问题映射在图上,映射在多维空间上
2、理解梯度下降公式:x = x - αg(x),g(x)为f(x)的导数
3、梯度下降公式中的x = x - αg(x),- αg(x)在实验中的表现是什么?
由初始点向最优点靠近:将x的值,从1,穿越0,由正到负,然后最后到达最优解-1.5旁边
一般的x和步子的正相关性:αg(x)是和x相关的函数,一般是x越大,|αg(x)|越大,αg(x)变化的越快,寻找梯度的步子迈的越大
4、梯度下降实例(要多看代码)?
比如求f(x) = x2+3x+4 的最优解
# -*- coding: utf-8 -*- # @Desc : 梯度下降计算函数的极小值 """ f(x) = x^2 + 3x + 4 f(x)的导数 g(x) = 2x + 3 """ def test(): def derivative(x_pre): # f(x)的导数 return 2 * x_pre + 3 x_pre = -5 # 初始值 x_now = 1 # 梯度下降初始值 alpha = 0.01 # 学习率,即步长 pression = 0.00001 # 更新的阀值 count = 0 # 统计迭代次数 while abs(x_now - x_pre) > pression: # print(x_now,'------------',x_pre) x_pre = x_now # x = x - αg(x),g(x)为f(x)的导数 x_now = x_pre - alpha * derivative(x_pre) count += 1 print(x_now) print(count) test()
5、梯度下降法只能对线性函数起作用么?
并不是:对所连续的有曲线都起作用
二、机器学习案例——梯度下降与逻辑回归简单实例
转自或参考:机器学习案例——梯度下降与逻辑回归简单实例
https://blog.csdn.net/heuguangxu/article/details/80495268
梯度下降实例
下图是f(x) = x2+3x+4 的函数图像,这是初中的一元二次函数,它的导数为g(x) = f’(x) = 2x+3。我们很明确的知道,当x = -1.5时,函数取得最小值。
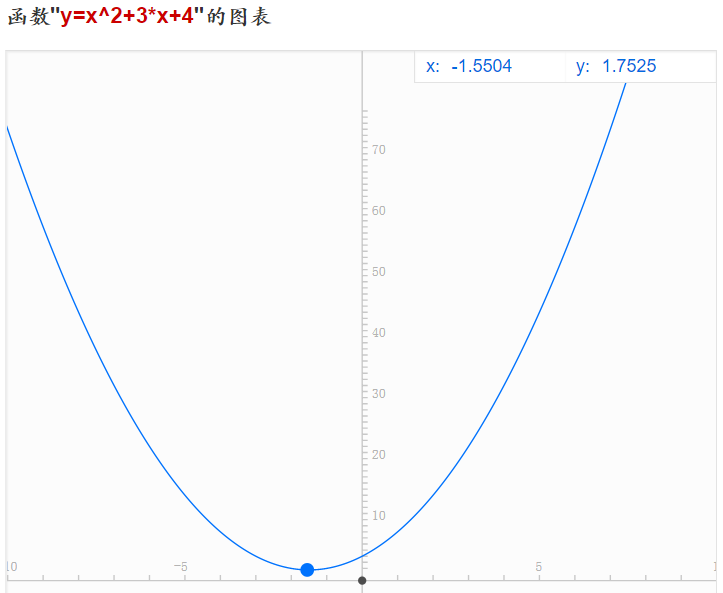
下面就通过梯度下降法来计算函数取最小值时x的取值。
# @Desc : 梯度下降计算函数的极小值
"""
f(x) = x^2 + 3x + 4
f(x)的导数 g(x) = 2x + 3
"""
def test():
def derivative(x_pre): # f(x)的导数
return 2 * x_pre + 3
x_pre = -5 # 初始值
x_now = 1 # 梯度下降初始值
alpha = 0.01 # 学习率,即步长
pression = 0.00001 # 更新的阀值
count = 0 # 统计迭代次数
while abs(x_now - x_pre) > pression:
x_pre = x_now
# x = x - αg(x),g(x)为f(x)的导数
x_now = x_pre - alpha * derivative(x_pre)
count += 1
print(x_now)
print(count)
# 结果
-1.4995140741236221
423可以看出,已经非常逼近真实的极值-1.5了,总共经过了423次迭代,逻辑回归中的梯度下降也是这样的,只不过函数没这么简单而已。
逻辑回归实例
自己在编写代码过程中,使用的是机器学习案例——鸢尾花数据集分析中提到的鸢尾花数据集,我把其中一个类别删除了,只留下了两个类别。经过训练后,得到参数如下图所示。
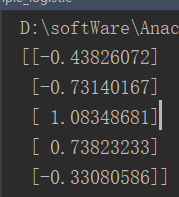
上面的数据有4个特征,不太好展示,因此重新用了别人家的数据,代码无需变动。建议还是参考别人写的更详细(地址在文章末尾),最后得到的参数是下面这个样子的,画出来的拟合效果还是不错的,为了不影响阅读代码贴在最后了。
[[-0.47350404]
[ 0.74213291]
[-5.47457118]]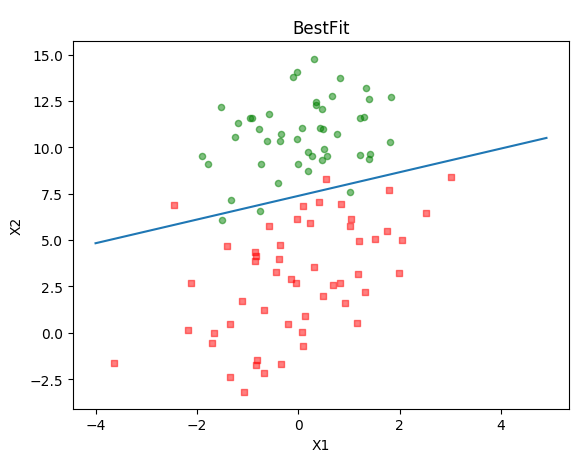
参考内容:
https://github.com/apachecn/MachineLearning/blob/master/src/py2.x/ML/5.Logistic/logistic.py
http://cuijiahua.com/blog/2017/11/ml_6_logistic_1.html
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
alpha = 0.001 # 学习率
iteration = 5000 # 迭代次数
# 加载数据集
def load_data():
# 读入数据
df = pd.read_csv('test.csv')
# 取label标签
Y_train = np.mat(df['class'])
# 将行向量转换为列向量
Y_train = np.mat(Y_train)
Y_train = Y_train.T
# 删除最后一列,即删除标签列
df.drop('class', axis=1, inplace=True)
# 添加一列,当b吧,方便计算,初始化为1
df['new'] = 1
X_train = np.mat(df)
return X_train, Y_train
# 返回最后训练的参数
def gradient_descent(X_train, Y_train):
row, col = X_train.shape
# 初始化,全为0
W = np.zeros((col, 1))
# 进行max_iteration次梯度下降
for i in range(iteration):
# 直接使用numpy提供的tanh函数
h = np.tanh(np.dot(X_train, W))
error = Y_train + h
# 梯度下降
W = W - alpha * np.dot(X_train.T, error)
return W.getA()
# 这段代码来抄自https://github.com/apachecn/MachineLearning/blob/master/src/py2.x/ML/5.Logistic/logistic.pyu
def plot_show(W):
X_train, Y_train = load_data()
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(X_train.shape[0]):
if int(Y_train[i]) == 1:
xcord1.append(X_train[i, 0])
ycord1.append(X_train[i, 1])
else:
xcord2.append(X_train[i, 0])
ycord2.append(X_train[i, 1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)
ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)
x = np.arange(-4.0, 5.0, 0.1)
"""
函数原型是:f(x) = w0*x0 + w1*x1 + b
x1在这里被当做y值了,f(x)被算到w0、w1、b身上去了
所以有:w0*x0 + w1*x1 + b = 0
可以得到:(b + w0 * x) / -w1
"""
y = (W[2] + W[0] * x) / -W[1]
ax.plot(x, y)
plt.title('BestFit')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
if __name__ == '__main__':
X_train, Y_train = load_data()
# print(Y_train)
W = gradient_descent(X_train, Y_train)
print(W)
plot_show(W)