2020 省选模拟测试 Round #10 solution (20/02/09)

【比赛链接】http://59.61.75.5:8018/contest/220

A. 逆序对

【题意】求所有大小为 $n$ 的排列的逆序对数目的 $k$ 次方的和。

【数据范围】$1le nle 10^7,1le k le 100$。

【题解】

一般这种 $k$ 次方和的题目可以用插值的方法做。最经典的就是 $sumlimits_{i=1}^{n} i^k$。本题类似。

考虑 $dp$，设 $f_{i,j}$ 为大小为 $i$、逆序对个数为 $j$ 的排列个数。转移有：$$f_{i,j}=sumlimits_{k=0}^{i-1}f_{i-1,j-k}$$

记 $g_i=sum_{j=0}^{frac{i(i-1)}{2}} f_{i,j}j^K$. 可以证明，$frac{g_n}{(n-2K)!}$ 是个 $O(K)$ 阶多项式。直接插值即可。

效率 $O(n+k^3)$。期望得分：100。

【代码】

#include<bits/stdc++.h>
const int mod=1000000007;
int inv[500],f[500][80010],n,k,Y[500],ans;
inline int power ( int x,int y )
{
    int z=1;
    for ( ;y;y>>=1,x=1LL*x*x%mod ) if ( y&1 ) z=1LL*z*x%mod;
    return z;
}
signed main()
{
    scanf("%d%d",&n,&k);
    f[0][0]=inv[0]=inv[1]=1;
    for ( int i=1;i<=4*k;i++ ) for ( int j=0;j<=i*(i-1)/2;j++ )
    {
        if ( j ) f[i][j]=f[i][j-1];
        f[i][j]=(f[i][j]+f[i-1][j])%mod;
        if ( j>=i ) f[i][j]=(f[i][j]-f[i-1][j-i]+mod)%mod;
    }
    for ( int i=2;i<=4*k;i++ ) inv[i]=1LL*inv[mod%i]*(mod-mod/i)%mod;
    for ( int i=3;i<=4*k;i++ ) inv[i]=1LL*inv[i-1]*inv[i]%mod;
    for ( int i=1;i<=4*k;i++ )
    {
        int res=0;
        for ( int j=0;j<=i*(i-1)/2;j++ ) res=(res+1LL*f[i][j]*power(j,k))%mod;
        Y[i]=1LL*res*inv[i]%mod;
    }
    if ( n<=4*k ) ans=Y[n];
    else for ( int i=1;i<=4*k;i++ )
    {
        int val=1;
        for ( int j=1;j<=4*k;j++ ) if ( j!=i ) val=1LL*val*(n-j)%mod*power((i-j+mod)%mod,mod-2)%mod;
        ans=(ans+1LL*val*Y[i])%mod;
    }
    for ( int i=1;i<=n;i++ ) ans=1LL*ans*i%mod;
    return !printf("%d
",ans);
}

B. 线段树

【题意】

一般地，线段树的结构如下：根为 $[1,n]$，对所有节点 $[l,r]$ $(l<r)$, 我们可以选取任意的 $m$ $(lle m<r)$ 并将区间劈作 $[l,m]$ 与 $[m+1,r]$ 两段，作为它的两个儿子。

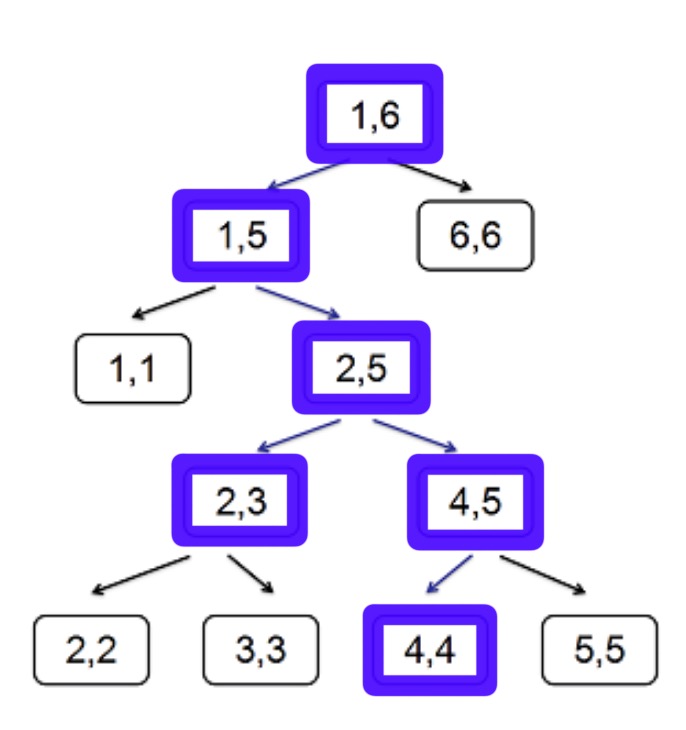
在上面的线段树中，若询问 $[2,4]$，我们会访问线段树中的这些蓝色节点。

给出 $m$ 个询问，你需要确定一种线段树的结构，使每次询问访问的节点个数的和最小。

【数据范围】$1le nle 500,\, 1le mle 2 imes 10^5,\, 1le l_ile r_ile n$。

【题解】

显然考虑区间 $dp$。考虑选择区间 $[i,j]$ 的权值 $w[i][j]$。

分类讨论询问区间与选择区间的相交情况，前缀和后缀和记录一下即可。

效率 $O(n^3)$。期望得分：100。

【代码】

#include<bits/stdc++.h>
int n,m,L[600],R[600],cnt[600],sum[600],val[600],w[600][600],f[600][600];
std::vector<int> G[600];
signed main()
{
    scanf("%d%d",&n,&m);
    for ( int x,y,Q=m;Q--; ) scanf("%d%d",&x,&y),L[x]++,R[y]++,cnt[x]++,cnt[y+1]--,G[y].push_back(x);
    for ( int i=1;i<=n;i++ ) cnt[i]+=cnt[i-1],R[i]+=R[i-1];
    for ( int i=n;i;i-- ) L[i]+=L[i+1];
    for ( int r=n;r;r-- )
    {
        for ( int x:G[r] ) val[x]++;
        for ( int l=1;l<r;l++ ) sum[l]=sum[l-1]+val[l];
        for ( int l=1;l<r;l++ ) w[l][r]=m-2*sum[l]-R[l-1]-L[r+1];
    }
    for ( int i=1;i<=n;i++ ) f[i][i]=cnt[i];
    for ( int r=2;r<=n;r++ ) for ( int l=r-1;l;l-- )
    {
        f[l][r]=1<<29;
        for ( int k=l;k<r;k++ ) f[l][r]=std::min(f[l][r],f[l][k]+f[k+1][r]+w[l][r]);
    }
    return !printf("%d
",f[1][n]);
}

C. 道路修建

【题意】

平面上有 $n+m$ 个整点，其中 $n$ 黑 $m$ 白。

现在要在黑点与白点间分别修路。显然，只需要 $n+m−2$ 条线段就可以让黑点与白点各自连通。

求一种连边方案，使在满足连通性的同时，任意两条线段都不在端点以外的地方相交。

【数据范围】$n>1,m>1$ 且 $n+m≤3000$。

【题解】

计算几何永远放 $T3$。显然是类似平面图分治的做法。

考虑先求出凸包。分析凸包上的点的颜色分布情况。

如果凸包上的点颜色段超过两段，可以证明（画图）无解。

考虑只有两段的情况。根据平面图分治的思想，进行三角剖分，对每个三角形分别解决。

考虑如何三角剖分。若三角形三个顶点同色，则这种剖分是无意义的，可能导致无解。

考虑强制使三个点异色。在凸包上的两个颜色连续段分别将每条线段与另一个颜色连续段的首个点连边构成三角形。画图发现这样可以满足条件。

对于凸包上的点全部同色的情况，可以在凸包内找一个点，向每条凸包上的线段连边构成三角形。

现在考虑三角形如何处理。设三角形顶点为 $u,v,w$，其中 $u$ 是颜色不同的点。

考虑三角形中点的颜色。如果全部与 $v,w$ 同色则直接连边即可。

若存在一个点 $p$ 与 $u$ 同色，分治 $(v,u,p),(w,u,p),(p,v,w)$ 三部分即可。

效率 $O(n^2)$。期望得分：100。

【代码】

#include<bits/stdc++.h>
inline int read ( void )
{
    int x=0;char ch;bool f=true;
    while ( !isdigit(ch=getchar()) ) if ( ch=='-' ) f=false;
    for ( x=ch^48;isdigit(ch=getchar()); ) x=(x<<1)+(x<<3)+(ch^48);
    return f ? x : -x ;
}
typedef struct { int x,y,c,id; } Point;
std::vector<Point> G,B;
std::vector<std::pair<Point,Point>> Ans;
Point st[3010];
inline long long cross ( Point u,Point v,Point w ) { return 1LL*(u.x-w.x)*(v.y-w.y)-1LL*(u.y-w.y)*(v.x-w.x); }
inline bool operator == ( Point u,Point v ) { return u.c==v.c and u.id==v.id ; }
inline bool Inside ( Point p,Point u,Point v,Point w )
{
    if ( p==u or p==v or p==w ) return false;
    bool f_uv=cross(u,v,p)>0,f_vw=cross(v,w,p)>0,f_wu=cross(w,u,p)>0;
    return f_uv==f_vw and f_vw==f_wu ;
}
inline void solve ( std::vector<Point> Points,Point u,Point v,Point w )
{
    if ( Points.empty() ) return;
    Point pos=(Point){0,0,0,-1};
    for ( auto p:Points ) if ( p.c==u.c ) { pos=p;break; }
    if ( ~pos.id )
    {
        Ans.push_back(std::make_pair(u,pos));
        std::vector<Point> Points_uv,Points_vw,Points_wu;
        for ( auto p:Points )
            if ( Inside(p,u,v,pos) ) Points_uv.push_back(p);
            else if ( Inside(p,v,w,pos) ) Points_vw.push_back(p);
            else if ( Inside(p,w,u,pos) ) Points_wu.push_back(p);
        solve(Points_uv,v,u,pos);
        solve(Points_wu,w,u,pos);
        solve(Points_vw,pos,v,w);
        return;
    }
    for ( auto p:Points ) Ans.push_back(std::make_pair(w,p));
}
signed main()
{
    int cntA=read(),cntB=read(),tp=0;
    for ( int i=1,x,y;i<=cntA;i++ ) x=read(),y=read(),G.push_back((Point){x,y,0,i});
    for ( int i=1,x,y;i<=cntB;i++ ) x=read(),y=read(),G.push_back((Point){x,y,1,i});
    std::sort(G.begin(),G.end(),[&](const Point &p1,const Point &p2){return p1.x==p2.x ? p1.y<p2.y : p1.x<p2.x;});
    st[tp=1]=G[0];
    for ( auto p:G )
    {
        while ( tp>1 and cross(p,st[tp],st[tp-1])<=0 ) tp--;
        st[++tp]=p;
    }
    for ( int i=1;i<=tp;i++ ) B.push_back(st[i]);
    st[tp=1]=G[0];
    for ( auto p:G )
    {
        while ( tp>1 and cross(p,st[tp],st[tp-1])>=0 ) tp--;
        st[++tp]=p;
    }
    for ( int i=tp-1;i>=2;i-- ) B.push_back(st[i]);
    int Dcnt=(B[0].c!=B[(int)B.size()-1].c);
    for ( int i=1;i<(int)B.size();i++ ) if ( B[i].c!=B[i-1].c ) Dcnt++;
    if ( Dcnt>2 ) return !puts("-1");
    if ( !Dcnt )
    {
        for ( int i=1;i<(int)B.size();i++ ) Ans.push_back(std::make_pair(B[i-1],B[i]));
        Point pos=(Point){0,0,0,-1};
        B.push_back(B[0]);
        for ( auto p:G ) if ( p.c!=B[0].c ) { pos=p;break; }
        for ( int i=1;i<(int)B.size();i++ )
        {
            std::vector<Point> Points;
            for ( auto p:G ) if ( Inside(p,B[i-1],B[i],pos) ) Points.push_back(p);
            solve(Points,pos,B[i-1],B[i]);
        }
    }
    else
    {
        std::vector<int> D;
        std::vector<Point> L,R;
        for ( int i=1;i<(int)B.size();i++ ) if ( B[i].c!=B[i-1].c ) D.push_back(i);
        if ( B[0].c!=B[(int)B.size()-1].c ) D.push_back((int)B.size());
        for ( int i=D[0];i<D[1];i++ ) L.push_back(B[i]);
        for ( int i=D[1];i<(int)B.size();i++ ) R.push_back(B[i]);
        for ( int i=0;i<D[0];i++ ) R.push_back(B[i]);
        for ( int i=1;i<(int)L.size();i++ )
        {
            Ans.push_back(std::make_pair(L[i-1],L[i]));
            std::vector<Point> Points;
            for ( auto p:G ) if ( Inside(p,L[i-1],L[i],R[0]) ) Points.push_back(p);
            solve(Points,R[0],L[i-1],L[i]);
        }
        for ( int i=1;i<(int)R.size();i++ )
        {
            Ans.push_back(std::make_pair(R[i-1],R[i]));
            std::vector<Point> Points;
            for ( auto p:G ) if ( Inside(p,R[i-1],R[i],L[0]) ) Points.push_back(p);
            solve(Points,L[0],R[i-1],R[i]);
        }
    }
    std::sort(Ans.begin(),Ans.end(),[&](const std::pair<Point,Point> &u,const std::pair<Point,Point> &v){return u.first.c<v.first.c;});
    for ( auto p:Ans ) printf("%d %d
",p.first.id,p.second.id);
    return 0;
}