CodeForces

题目：

Adding two numbers several times is a time-consuming task, so you want to build a robot. The robot should have a string S=S1S2…SNS=S1S2…SN of NN characters on its memory that represents addition instructions. Each character of the string, SiSi, is either 'A' or 'B'.

You want to be able to give QQ commands to the robot, each command is either of the following types:

• 1 LL RR. The robot should toggle all the characters of SiSi where L≤i≤RL≤i≤R. Toggling a character means changing it to 'A' if it was previously 'B', or changing it to 'B' if it was previously 'A'.
• 2 LL RR AA BB. The robot should call f(L,R,A,B)f(L,R,A,B) and return two integers as defined in the following pseudocode:

      function f(L, R, A, B):
        FOR i from L to R
          if S[i] = 'A'
            A = A + B
          else
            B = A + B
        return (A, B)
    

You want to implement the robot's expected behavior.

Input

Input begins with a line containing two integers: NN QQ (1≤N,Q≤1000001≤N,Q≤100000) representing the number of characters in the robot's memory and the number of commands, respectively. The next line contains a string SS containing NN characters (each either 'A' or 'B') representing the initial string in the robot's memory. The next QQ lines each contains a command of the following types.

• 1 LL RR (1≤L≤R≤N1≤L≤R≤N)
• 2 LL RR AA BB (1≤L≤R≤N1≤L≤R≤N; 0≤A,B≤1090≤A,B≤109)

There is at least one command of the second type.

Output

For each command of the second type in the same order as input, output in a line two integers (separated by a single space), the value of AA and BB returned by f(L,R,A,B)f(L,R,A,B), respectively. As this output can be large, you need to modulo the output by 10000000071000000007.

Example

Input

5 3
ABAAA
2 1 5 1 1
1 3 5
2 2 5 0 1000000000

Output

11 3
0 1000000000

Note

Explanation for the sample input/output #1

For the first command, calling f(L,R,A,B)f(L,R,A,B) causes the following:

• Initially, A=1A=1 and B=1B=1.
• At the end of i=1i=1, A=2A=2 and B=1B=1.
• At the end of i=2i=2, A=2A=2 and B=3B=3.
• At the end of i=3i=3, A=5A=5 and B=3B=3.
• At the end of i=4i=4, A=8A=8 and B=3B=3.
• At the end of i=5i=5, A=11A=11 and B=3B=3.

Therefore, f(L,R,A,B)f(L,R,A,B) will return (11,3)(11,3).

For the second command, string SS will be updated to "ABBBB".

For the third command, the value of AA will always be 00 and the value of BB will always be 10000000001000000000. Therefore, f(L,R,A,B)f(L,R,A,B) will return (0,1000000000)(0,1000000000).

题意：

　　给你长度为n的字符串，只有A和B两种字符，有两种操作。

　　1.给定区间[l,r]，把区间内的A变成B，B变成A

　　2.给定区间[l,r]，还有2个数x，y，区间从左到右，如果s[i] = 'A' 则x = x + y，如果s[i] = 'B'则y = x + y。问最后x和y各是多少（mod1e9+7）。

思路：

　　首先观察x=x+y，y=x+y这两个式子

　　如果字符是A，则x = x + y，y = 0 * x + y

　　如果字符是B，则x = x + 0 * y， y = x + y

　　看出有个系数关系，可用矩阵表示

　　

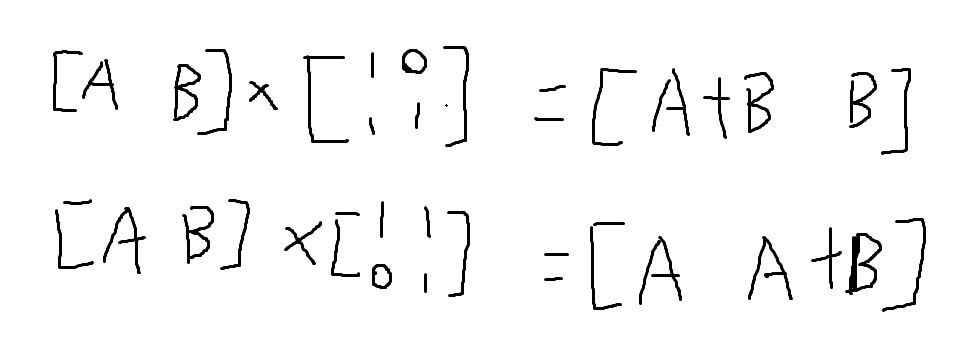
　　即用矩阵乘法计算x和y的最终结果，矩阵的乘积可以用线段树维护。

　　关于第二个操作，即翻转字符

　　假设前者的结果是 x = ax + by  y = cx + dy

　　A的意思是把x+y的值赋给x，B的意思是把x+y的值赋给y

　　翻转之后A和B的位置刚好变换,那么最后肯定是x和y的系数互换。

　　当然也可以把后者的y看成x，x看成y（换元法），遵循这个思路把前者的x和y替换掉，得到 y = ay +bx    x=cy+dx

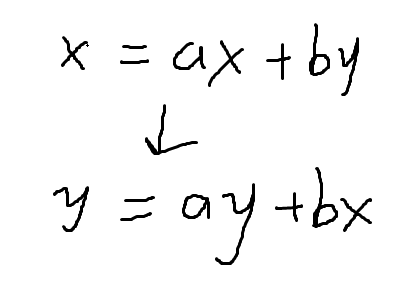　　(另一个数同理)

　　对比一下结果，容易发现翻转一个序列 = 区间矩阵乘积内的数交叉互换

　　

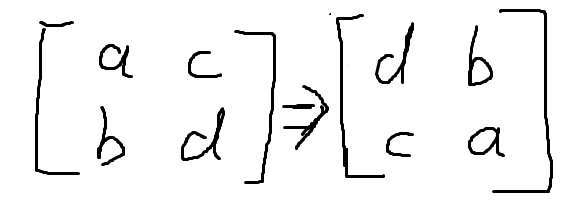
 　　当然也可以写出AA和BB的结果，对比一下找找规律。

代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 7;
const int mod = 1e9 + 7;
struct node {
    ll mx[2][2];
    node(ll a=0,ll b=0,ll c=0,ll d=0) {
        mx[0][0] = a;
        mx[0][1] = b;
        mx[1][0] = c;
        mx[1][1] = d;
    }
    node operator * (const node b) const {
        node c = node(0,0,0,0);
        for (int i=0; i<2; ++i)
            for (int j=0; j<2; ++j)
                for (int k=0; k<2; ++k) 
                    c.mx[i][j] = (c.mx[i][j] + mx[i][k] * b.mx[k][j] % mod) % mod;
        return c;
    }
    void nswap() {
        swap(mx[0][0],mx[1][1]);
        swap(mx[0][1],mx[1][0]);
    }
}tr[maxn<<3];

int n,q,x,l,r,lz[maxn<<3];
ll a,b;
char s[maxn];
void pushdown(int rt) {
    if(lz[rt]) {
        tr[rt].nswap();
        lz[rt<<1] ^= 1;
        lz[rt<<1|1] ^= 1;
        lz[rt] = 0;
    }
}
void build(int l,int r,int rt) {
    if(l == r) {
        if(s[l] == 'A') tr[rt] = node(1,0,1,1);
        else tr[rt] = node(1,1,0,1);
        return;
    }
    int mid = l + r >> 1;
    build(l,mid,rt<<1);
    build(mid+1,r,rt<<1|1);
    tr[rt] = tr[rt<<1] * tr[rt<<1|1];
}
void update(int l,int r,int rt,int L,int R) {
    pushdown(rt);
    if(L<=l && r<=R) {
        lz[rt] ^= 1;
        return;
    }
    int mid = l + r >> 1;
    if(L<=mid) update(l,mid,rt<<1,L,R);
    if(mid<R) update(mid+1,r,rt<<1|1,L,R);
    if(l!=r) {
        pushdown(rt<<1);
        pushdown(rt<<1|1);
        tr[rt] = tr[rt<<1] * tr[rt<<1|1];
    }
}

node query(int l,int r,int rt,int L,int R) {
    pushdown(rt);
    if(L<=l&&r<=R) return tr[rt];
    int mid = l + r >> 1;
    node ans = node(1,0,0,1);
    if(L<=mid) ans = ans * query(l,mid,rt<<1,L,R);
    if(mid<R) ans = ans * query(mid+1,r,rt<<1|1,L,R);
    return ans;
}

int main() {
    scanf("%d%d",&n,&q);
    scanf("%s",s+1);
    build(1,n,1);
    while(q--) {
        scanf("%d",&x);
        if(x == 1) {
            scanf("%d%d",&l,&r);
            update(1,n,1,l,r);
        }
        else {
            scanf("%d%d%lld%lld",&l,&r,&a,&b);
            node c = query(1,n,1,l,r);
            ll A = (a * c.mx[0][0] % mod + b * c.mx[1][0] % mod) % mod;
            ll B = (a * c.mx[0][1] % mod + b * c.mx[1][1] % mod) % mod;
            printf("%lld %lld
",A,B);
        }
    }
    return 0;
}