题目:
杭州人称那些傻乎乎粘嗒嗒的人为62(音:laoer)。
杭州交通管理局经常会扩充一些的士车牌照,新近出来一个好消息,以后上牌照,不再含有不吉利的数字了,这样一来,就可以消除个别的士司机和乘客的心理障碍,更安全地服务大众。
不吉利的数字为所有含有4或62的号码。例如:
62315 73418 88914
都属于不吉利号码。但是,61152虽然含有6和2,但不是62连号,所以不属于不吉利数字之列。
你的任务是,对于每次给出的一个牌照区间号,推断出交管局今次又要实际上给多少辆新的士车上牌照了。
Inpu
t输入的都是整数对n、m(0<n≤m<1000000),如果遇到都是0的整数对,则输入结束。
Output
对于每个整数对,输出一个不含有不吉利数字的统计个数,该数值占一行位置。
Sample Input
1 100
0 0
Sample Output
80
题意:给出2个数n,m 且 n<=m,问区间【n,m】中有多少个不包含4和不包含连续的62的数。
暴力枚举就超时了,下面介绍一下数位DP
数位DP也就是一个记忆化搜索的过程,其实也就是模拟数数的过程(深搜)
举个栗子,我们正常从1到5123数数
就相当于数0001,0002,.....0010,0011,0012......1000....5123这样一个一个数
而数位DP,就是按个位,十位,百位,按位来数
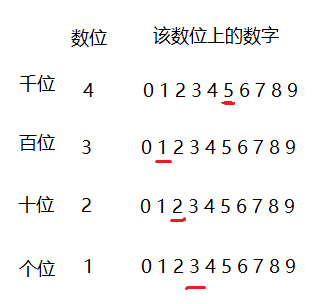
思想是这样的,假设n=1,m=5123
上面划线的数字组合起来就表示5123
我们定义,dp【20】【2】
digit【20】//把数字的每一个数位存起来,对5123来说,digit【1】=3,digit【2】=2,digit【3】=1,digit【4】=5,
解释:dp【i】【1】表示当数位i+1的数字是6时候,数位i有多少个不包含4和不包含62的数
dp【i】【0】表示当数位i+1的数字不是6时候,数位i有多少个不包含4和不包含62的数
比如dp【1】【0】= 9(当数位2,即十位的数字不是6时,个位可以提供的数字有0,1,2,3,5,6,7,8,9共9个)
dp【1】【1】= 8(当数位2,即十位的数字是6是,个位可以提供的数字有0,1,3,5,6,7,8,9共8个)
我们先跑一遍位数是1的数,更新dp【1】【1】和dp【1】【0】
当我们跑到十位0时,因为这时候的数字是0,不是6,所以十位数是0的贡献是dp【1】【0】=9
同理,当十位是1,2,3,5,7,8,9是,贡献都是dp【1】【0】=9
十位是4的时候,因为不能出现数字4,所以它的贡献是0
十位是6的时候,贡献是dp【1】【1】=8(60,61,63,65,66,67,68,69共8个)
更新一下dp【2】【0】
它的值就应该是十位数字0,1,2,3,5,6,7,8,9贡献之和,即9*8+8=80
再更新一下dp【2】【1】
它的值就应该是十位数字0,1,3,5,6,7,8,9贡献之和,即9*7+8=71
这样就可以一直更新上去
把各个数位上的数字贡献记录下来,提供给更高位的数位,这样就实现了记忆化搜索
当然还有边界问题
当我们千位是5的时候,千位(最高位)的数字到了最大值,百位就只能看0和1的贡献
百位数字为0的贡献可以直接利用,因为5000-5099都在1-5125的范围内
但1是百位的最大值(在千位是最高位的前提下),不能直接利用百位是1的贡献(5100-5199有部分数超过了5123)
所以十位是0,1的贡献可以直接利用,十位是2的贡献不能直接利用
只需要特判一下就可以了
这个过程还是听视频讲解的好(画图要画好多张啊,偷懒偷懒)
推荐一个视频 https://www.bilibili.com/video/av27156563?t=2383
博主也是看了这位大佬的视频才理解了数位dp(当然下面的代码也是这位大佬的)
代码实现:(详细看注释)

ll dfs(int len,bool if6,bool limit) {/*len表示当前的数位,if6表示上一个数位的数字是不是6,limit表示比现在数位高的数位是不是都到了最大值,即限制值,如千位是5,百位是1,那么十位就只能取0,1,2,起到了限制作用*/ if(len==0) return 1;//递归边界 if(!limit && dp[len][if6]) return dp[len][if6]; /*提速部分,如果没有被限制而且dp数组已经更新,则直接使用dp数组*/ ll cnt=0,up_bound=(limit?digit[len]:9); /*cnt用来计数,up_bound表示上界,如果高位没有被限制,则该位可以是数字0到9,否则该位数字是0到digit【len】,对于十位来说就是0到2(假如千位是5,百位是1,高位限制了)*/ for(int i=0;i<=up_bound;++i){ if(if6 && i==2) continue;//上一位数字是6而且当前位数数字是2,忽略 if(i==4) continue;//当前数位数字是4,忽略 cnt+=dfs(len-1,i==6,limit&&i==up_bound); /*下一个数位的各个数字贡献之和就是当前位数数字是i的贡献,第三个参数表示当前数位和高数位是不是都达到了限制值*/ } if(!limit) dp[len][if6]=cnt; /*没有被限制的数位计算出的cnt才能代表整个数位的贡献,否则会有残缺*/ return cnt; } ll solve(ll num) { int k=0; while(num)//分解num各个数位上的数字 { digit[++k]=num%10; num/=10; } return dfs(k,0,1); /*从高位开始向低位搜索,最高的数自然是自己本身,它的上一位只能是0,不是6,所以第二个参数写0,因为没有15123,只有05123,所以第三个参数写1*/ }
AC代码:

#include <bits/stdc++.h> using namespace std; typedef long long int ll; int digit[20]; ll dp[20][2]; ll dfs(int len,bool if6,bool limit) { if(len==0) return 1; if(!limit && dp[len][if6]) return dp[len][if6]; ll cnt=0,up_bound=(limit?digit[len]:9);//上界; for(int i=0;i<=up_bound;++i){ if(if6 && i==2) continue; if(i==4) continue; cnt+=dfs(len-1,i==6,limit&&i==up_bound); } if(!limit) dp[len][if6]=cnt; return cnt; } ll solve(ll num) { int k=0; while(num) { digit[++k]=num%10; num/=10; } return dfs(k,0,1); } int main() { ll n,m; while(cin>>n>>m) { memset(dp,0,sizeof(dp)); if(n==0&&m==0) break; cout<<solve(m)-solve(n-1)<<' '; } return 0; }