一:关于一些初步的优化方法
以下内容将根据两道经典例题来说明
首先是素数的判断,相信同学们都是深有体会的。该问题本质上是穷举法的判断,循环判断质因子最终得到结果。实际上在面对一些低位的数据的判断时,运行时间往往是能使人接受的,但是当面对高位数据的处理时,往往会使人头疼,正如笔者以及许多同学在提交时遇到的一个测试点超时的问题,此时应该是第一次涉及到优化的问题了,当然由于老师课堂上并未涉及到过多优化的问题,因此笔者在此给出一些个人理解,希望能抛砖引玉,谢谢。
首先给出一段未优化的代码:(注:笔者未特判1,略去不计)
#include<stdio.h>
#include<time.h> //调用系统时间函数判断实际运行时间
#include<math.h>
int start = 0,end = 0; //定义全局变量来记录实际的开始运行时间以及实际结束时间
int prime(int max); //声明一个整型函数prime来判断质数
int main(void)
{
int max = 0,i = 0;
scanf("%d",&max);
start = clock(); //此处调用系统时间函数记录开始时间,未包括用户输入时间
prime(max); //调用质数判断函数
end = clock(); //调用系统时间函数记录质数判断函数结束的时间
printf("
%d ms",end - start); //输出前后时间差,单位为毫秒(ms)
return 0;
}
int prime(int max)
{
int i = 0,j = 0;
for(i = 2;i <= max;i++)
{
for(j = 2;j < i;j++)
{
if(i % j == 0)
{
break;
}
}
if(j == i)
{
printf("%d ",i);
}
}
}
接下来给出几组数据的测试图片,分别是对应一千,一万,十万以及1000000以及以内的质数的判断,对应测试平台均为x86架构的i7-7700hq以及16g ddr4 2400 Mhz内存,测试时间均为多次测试取均值。
未优化代码:一千及以内素数判断:
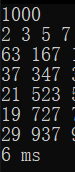
一万以内:
十万以内:
一百万以内:
可以看到,对应低位的,即十万以内的数值的处理,其运算速度还足以令人接受,弹一旦到了百万级,尤其是千万级的运算,速度就不那么令人满意了,一根烟都快抽完了...咳咳...
实际上,这种结果也是在预想之内的,数量级每提高一位,对应的运算次数却是指数级上升的,因此时间的提升速度也会相应以难以想象的程度增多。对于此类经典的数学问题,我们不妨就从数学角度入手,可以归纳出几点,对于一个数,其最小的因子除了1忽略不计,那即是2,那么因数为2的数,我们自然想到偶数,因此可以给出第一步优化,即在某数进入质数判断前判断其奇偶性,若其为偶数(2除外),可直接忽略不计,当然,这一过程由于优化效能并不高,因此可以不加以考虑。
此外,我们还可以考虑质数的另一性质,若其一半未找到除1以外的因子,那么该数即为质数,数学证明过程忽略...当然...数学能给出的另一范围为其开方数,那么结合这一点,我们可以给出初步优化的代码:
#include<stdio.h>
#include<time.h> //调用系统时间函数判断实际运行时间
#include<math.h>
int start = 0,end = 0; //定义全局变量来记录实际的开始运行时间以及实际结束时间
int prime(int max); //声明一个整型函数prime来判断质数
int main(void)
{
int max = 0,i = 0;
scanf("%d",&max);
start = clock(); //此处调用系统时间函数记录开始时间,未包括用户输入时间
prime(max); //调用质数判断函数
end = clock(); //调用系统时间函数记录质数判断函数结束的时间
printf("
%d ms",end - start); //输出前后时间差,单位为毫秒(ms)
return 0;
}
int prime(int max)
{
int i = 0,j = 0;
for(i = 2;i <= max;i++)
{
for(j = 2;j <= sqrt(i);j++) //此处对被判断数开方来缩小判断范围
{
if(i % j == 0)
{
break;
}
}
if(j > sqrt(i))
{
printf("%d ",i);
}
}
}
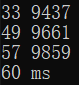
下为时间测试:
一千以内:
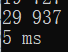
一万以内:
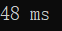
十万以内:
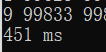
一百万以内:
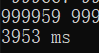
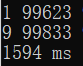
可以看到,对低位数据的处理提升并不明显,但是对高位数字,自十万开始的数据的处理速度明显提升了一截,百万级的处理时间更是只有优化前的 %4 左右,提升十分明显,最后笔者又用优化后的程序计算了千万级的数据,结果如图:
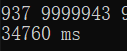
其运算时间仍然只有优化前代码运算百万级的时间的%35 左右,可见优化效能。
对于质数判断类的优化这次先到此为止,再多的方法有筛选法等,由于涉及到布尔值运算,因此在此不过多说明。
关于水仙花数(自幂类问题)
首先是题目要求 要求输入N 其后输出所有N位的水仙花数(即其各位的N次幂之和等于其本身),题目本身并不难,通过简单的结构即可求解,但是当笔者计算七位的水仙花数时,发现其运算效能十分低下,运行超时无法通过系统检验,遂开始考虑初步优化问题,先给出未优化的代码以及其运行结果:
#include<stdio.h>
#include<math.h> //调用数学函数计算幂
#include<time.h> //同样调用系统时间函数计算运行时间
long start = 0,end = 0;
int nass(int n); //声明一个判断水仙花数的函数
int main(void)
{
int N = 0;
scanf("%d",&N);
nass(N);
end = clock();
printf("%ld ms
",end - start);
return 0;
}
int nass(int n)
{
int min = 0,max = 0,i = 0,num = 0,flag = 0;
double sum = 0.0;
start = clock();
switch(n)
{
case 3:
min = 100;
max = 999;
break;
case 4:
min = 1000;
max = 9999;
break;
case 5:
min = 10000;
max = 99999;
break;
case 6:
min = 100000;
max = 999999;
break;
case 7:
min = 1000000;
max = 9999999;
}
for(i = min;i <= max;i++)
{
sum = 0;
flag = i;
while(flag != 0)
{
num = pow(flag % 10,n);
sum += num;
flag /= 10;
}
if(sum == i)
{
printf("%d
",i);
}
}
}
三位:
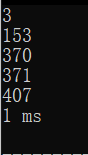
四位:
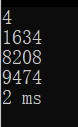
五位:
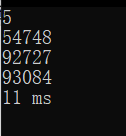
六位:
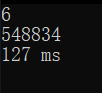
七位:
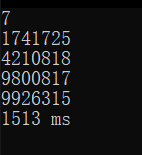
可以看到,当运到七位时这个时间十分恐怖,因此超时。于是笔者开始思考如何优化,但是比较起素数类问题,二者的主要区别在于可归纳性,对于素数,我们从数学定义上可以得到的信息十分多,因此优化手段自然很多,但是对于水仙花数,至少目前笔者找到的规律性基本上不存在的...因此我们只能从另一方面入手,即计算过程入手,而非缩小范围。
经过与助教老师的交流,得到了一个初步的解决思路,即简化计算过程,对于每一位数的N次幂,我们可以轻易地得到其解,而优化前的代码想法较为直接,但是反过来想,由于位数N以给定,次数也给定,我们在将位数传入函数时,自0到9的N次幂实际上已经确定,因而可以将其存储,在后续计算时直接将已有结果调用,即生成一个关于0~9的N次幂的乘法表,这样可以大大减少重复运算次数,做该步优化前好比是明明是跑100米就可以解决的问题,我却使其来回跑了数万次,因此浪费大量效能与时间。下面给出初步优化后的代码;
#include<stdio.h>
#include<math.h>
#include<time.h>
int start = 0,end = 0;
int nass(int n);
int main(void)
{
int N = 0;
scanf("%d",&N);
nass(N);
end = clock();
printf("%ld ms
",end - start);
return 0;
}
int nass(int n)
{
int min = 0,max = 0,i = 0,num = 0,flag = 0,number[10] = {0};
long long sum = 0;
start = clock();
for(i = 0;i <= 9;i++)
{
number[i] = pow(i,n);
}
switch(n)
{
case 3:
min = 100;
max = 999;
break;
case 4:
min = 1000;
max = 9999;
break;
case 5:
min = 10000;
max = 99999;
break;
case 6:
min = 100000;
max = 999999;
break;
case 7:
min = 1000000;
max = 9999999;
}
for(i = min;i <= max;i++)
{
sum = 0;
flag = i;
while(flag != 0)
{
num = number[flag % 10];
sum += num;
flag /= 10;
}
if(sum == i)
{
printf("%d
",i);
}
}
}
下面为测试图:
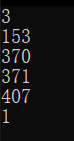
三位:
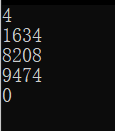
四位:
五位:
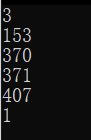
六位:
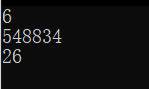
七位;
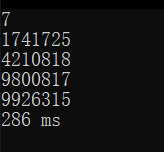
可以看到,提升还是十分明显的,差距从五位开始逐渐拉开,这是由于随位数的提升,搜索范围的扩大以及指数计算的位的提升的缘故,因此这张乘法表的提升效能对于高位的提升会越来越大,看起来这个结果已经很令人满意了,但是还不能止步于此,由于笔者又从老师那里得知 系统自带的数学库函数的计算默认转化为浮点型,而浮点运算相对于整型的运算实际上是要慢的,那么针对这一点,而又有一位学长告诉笔者,对于这种高位数的运算,可以考虑将int型改为long long int型,那么针对这几点,笔者再次进行了优化,代码如下:
#include<stdio.h>
long long int power(int number,int n); //此处改为自定幂函数计算函数
#include<time.h>
int start = 0,end = 0;
int nass(int n);
int main(void)
{
int N = 0;
scanf("%d",&N);
nass(N);
end = clock();
printf("%ld ms
",end - start);
return 0;
}
int nass(int n)
{
int min = 0,max = 0,i = 0,num = 0,flag = 0,number[10] = {0};
long long sum = 0;
start = clock();
for(i = 0;i <= 9;i++)
{
number[i] = power(i,n);
}
switch(n)
{
case 3:
min = 100;
max = 999;
break;
case 4:
min = 1000;
max = 9999;
break;
case 5:
min = 10000;
max = 99999;
break;
case 6:
min = 100000;
max = 999999;
break;
case 7:
min = 1000000;
max = 9999999;
}
for(i = min;i <= max;i++)
{
sum = 0;
flag = i;
while(flag != 0)
{
num = number[flag % 10];
sum += num;
flag /= 10;
}
if(sum == i)
{
printf("%d
",i);
}
}
}
long long int power(int number,int n)
{
int result = 1,i = 0;
for(i = 1;i <= n;i++)
{
result *= number;
}
return result;
}
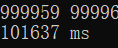
下面是测试图,由于低位已经不存在挑战性,故只给出6位及七位的结果:
六位:
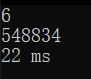
七位:
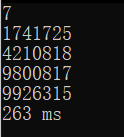
尽管效能提升并不是很明显,但是这些小的提升仍然令人满意,因为优化实际上是一个没有尽头的过程,对于程序而言,优化在任何时候都是十分有价值的过程,如果我们的计算机可以无限地快(当然这是一个伪命题),那么我们就没有必要进行优化了吗?答案是否定的,在任何时候浪费性能都是难以被接受的,实际上有人会问我们为什么要处理这些数字,看起来他们不存在什么特别的价值,与其浪费时间为了这么几个数字还不如去编写一个记录猪的产仔时间的程序,因为这些数字看起来并不能解决一些实际问题,当然 如果这么想的话那就大错特错了,这些数学上的一些具有一些独特性质的数字实际上在各种领域都存在不可估量的价值,尤其是涉及到加密领域,例如被熟知的高位素数,或是更有价值的梅森素数,现在一种较为靠谱的加密方式为将几个高位素数相乘,得到某个 数字,再将其作为密码,因为将数个素数相乘很简单,而将某个高位数字分解为数个素数的积却是异常困难的,这也就在一定程度上提高了密码的安全性。
对于优化,笔者现阶段将其分为两种思路,第一种是缩小范围的方法,例如上面提到的寻找素数,这种方法往往需要数学 上的一些性质,而这种方法的提升效能往往是较大的,对于一些穷举类的问题,我们先从一般性入手,最后通过分析找到其特殊性,往往可以在一定程度上缩小其范围,获得较大的提升。
而另一种思路,就是从过程入手,例如上面提到的水仙花数问题,我们既然无法缩小范围,那么我们从其运行过程入手,找到其重复性高的过程,对其进行简化处理,可以很大程度上减少计算机的工作量,从而提升效率。
对于优化这次先告一段落,下次如果有时间的话会介绍几种经典算法,例如欧几里得算法,素数筛选法等,当然如果有兴趣的话可以自己去了解。
另一方面是关于数组
本次主要针对一维数组,二维数组会略有涉及。
数组在C语言中是一大重点,可以说,数组与指针是C语言的核心所在,因此学好数组对未来的学习会提供很大的帮助,首先是一维组,我们可以简单将其理解为一条队伍,或是一个箱子,尽管这两个比喻都不大恰当,但是这种具象化的理解在处理一些问题时往往可以使问题简化。在计算机中,当一个一维数组被声明时,计算机就会为其开辟一块连续的内存,而数组名本身实际上是一个地址,即表示该数组的首个元素的地址,就好像是全校同学在操场上开全体大会时,若需要检查人员的到场情况,我们当然不会一个个点名,而是通过队伍排头所持的班牌先来寻找到该班级,之后在该班级的队伍中进行计数,相应的,每一个排头实际上就像是一维数组的数组名,可以想象成班号,这个班号就较有意思,它既可以表示整个队伍的班级,同时又可以表达该队伍所有成员所属的班级。
地址实际上是一个物理地址,即表示某内存单元在整个内存序列中的位置,而数组名本身又是个地址常量。指针是一种指向某物理地址的变量,那么,数组名本身也在某种程度上引用了一个指针,基于此,指针与数组的关联性相当的强,那么我们在像函数传递数组时,实际上是传递了存储有某类数据的一块连续内存的第一个地址,当然,同时传递的还有该数组的长度,否则函数就不知道该数组最后一个元素的位置,从而带有越界的危险。而C语言的一大缺陷就是其本身不会检查数组下标是否越界,这种越界有时是不明显的,但后果却是不可预知的,有时它可以看起来像是正常工作了,而有时它又会被赋予一个毫无意义的数值,而有时,它覆盖了某个运行进程中的重要数据,甚至会导致系统崩溃,因此检查数组下标是否越界是一个十分有必要的工作。
下面给出一段有问题的代码,并附上一段简单的函数,来检查是否存在越界风险:
#include<stdio.h>
#include<stdlib.h>
#define N 5 //定义一个宏常量来确定数组元素的长度
void check(int i); //自定义函数来检查元素个数是否超出数组实际长度
int main(void)
{
int num[N] = {0},n = 0,i = 0;
scanf("%d",&n);
check(n); //将用户选择输入的元素个数的值传给检查是否越界的函数
for(i = 0;i < n;i++)
{
scanf("%d",&num[i]);
}
for(i = n;i >= 0;i--) //实际上此处也有越界,如果有兴趣的话可以尝试改进该函数,改进方法有时间在下一次展示
{
printf("%d",num[i]);
}
return 0;
}
void check(int i)
{
if(i > N || i < 0) //对传入参数进行合法性检查
{
printf("Cross the border!!!"); //若有越界风险,会提示用户并强制结束程序
exit(0);
}
}
对于该函数,你可以进行一定程度的改进使其在任何对数组下标进行操作的位置使其发挥作用,虽然最好的方法是细心检查,但是当涉及大量数组操作以及大段程序的编写时,难免会出现错误,因此合理使用一些小的自定义函数可以省下许多心。
接下来是一个被同学们广泛反馈的问题,就是插入排序的问题,实际上该问题并不难理解,还是引用上文提到的队伍模型,假设某班同学集合跑操,其排列方式为按身高从高到底排列,即对应数组的升序,那么该序列在此时是有序的。如下图(为便于理解,笔者使用表格的方式来说明)。

此时队伍已经站好,为有序状态。但是在开跑前,很不幸,我被班长发现不在,此时我又赶到了,那么按照身高升序的原则,我需要找到一个合适的位置来插入队伍中,方法就是从队伍中找到比我矮的人(假设存在) ,那么我从F同学处开始比较,即数组的第0个元素,并从队伍尾端向前比较,即遍历数组元素,幸运的是,我发现F,E同学都比我矮,那么我需要做的就是站到E同学的前面,但是此时队伍并没有位置,因此D同学以及D同学之前的同学都需要向前移动一个人的位置以给我留出足够容纳我的空间,如下图:

很好,现在我的位置已经有了,剩下的就是使我插入该空位。

也许有人会问,使F和E同学向后移动一位不是更好吗,那么这就涉及到之前提到的问题,即数组下标越界。放到该例中可以理解为F同学后排是墙或是另外一个班级,显然,无论是哪种情形后果都是不幸的,当然,将我插入队伍本身也是带有风险的,例如队伍前排已占满同学,那么我就需要冒着A同学失踪的风险去插入队伍,因此,在使用该排序方式时仍然需要检查已有数组的长度是否足够容纳需要插入的元素。
另一方面是关于排序算法,关于几种 时间复杂度均为o(N^2)的排序算法,主要有选择排序以及冒泡排序,在此不再赘述,唯一要强调的就是排序算法的地位,可以说,排序算法是算法中十分具有价值的问题,在实际应用中十分广泛。因此希望同学能好好掌握。当然如果有时间的话笔者会以较为好理解的方式来介绍这几种算法。
二维数组...因为时间原因暂且鸽了...留下一张图吧...二维数组实际上是一维数组的延伸,只不过其在内存中存储的方式仍然是连续存储,可以将其想象为二维表,或将其理解为二维坐标。其基本结构如下,假设笔者定义了一个num[3][5]数组,那么其结构如下:

当然,需要注意的问题仍然只有一点,无论是长度还是宽度,其下标均是从0开始,谨记!!!
那么对应这种二维表的关系,我们可以使用其保存一些具有关联性的数据,如图:

我们可以用一个二维数组来存放一些学生信息,那么每一个列号为0的单元就可以存放学生信息,最简单的是学号,当然有兴趣的话可以思考一下如何存放姓名,那么对应每一个行号,例如我的行号为0,那么第0行就可以用来存放我的成绩(原谅我的无耻),这样,每一个人与其对应的列就有了一定的对应关系,例如要查询我的成绩,我只需要知道我的数据存放的行号即可,剩下的就是读取该行的所有数据,而除了第0列是用来存放姓名信息以外,其它列可以代表某一科目的成绩。
剩下的就是为二维数组赋值的问题,实际上同一维数组一样,我们需要动态赋值,只不过这一次是嵌套循环,即外层循环先选定某一行或某一列,内层循环负责该行或列的赋值,如下:
#include<stdio.h>
int main(void)
{
int score[3][5],i = 0,j = 0;
for(i = 0;i < 3;i++) //外层循环用以确定学号
{
for(j = 0;j < 5;j++) //内层用以确定该学号对应的各项成绩
{
scanf("%d",&score[i][j]);
}
}
for(i = 0;i < 3;i++)
{
for(j = 0;j < 5;j++)
{
printf("%d ",score[i][j]);
}
printf("
");
}
return 0;
}
该程序对应上文例子结果如图:(现以学号表示,有兴趣的话可以尝试输出前导零或学号,当然要用到字符串数组)
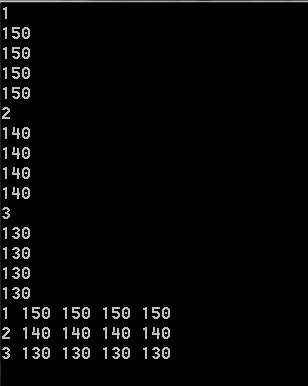
本次就到这里吧...最近都在被期末考试吓得惶惶不可终日,当然是先做一套高数压压惊。其实对于编程而言,重在理解,可能最初并不理解,但是不理解时可以尝试模仿,当模仿到一定程度,那么自然就记住了,等到使用了一定次数或程度后再回头看一下不理解的地方,会发现自己早已经理解了,使用起来也游刃有余,因此,有时间啃理论或者测试完沮丧,不如坐下来耐着性子写完一道题,学习编程确实有时会感到枯燥,笔者也经常一坐坐上五六个小时,但并不是毫无意义的,对于一些不理解的题当通过长时间的摸索最终得到正确解的时候的喜悦是难以言喻的,希望同学们能多体会,相信会有所收获,最后祝同学们期末考试顺利,笔者本人能力也有限,如果有问题的话可以随时来找我,前提是我有时间以及我会的情况下。
最后如发现文中有问题欢迎指正,不胜感激。