|—定位—|—蒙特卡洛方法(定位自身)
| |—卡尔曼滤波器(定位其他车辆)
|—高斯函数
|—循环两个过程—|—测量(测量更新)
| |—运动(预测值)
|—更高维度的高斯和卡尔曼
|—追踪的核心代码(一个二维卡尔曼滤波器)
卡尔曼滤波和蒙特卡洛定位方法主要区别:
- 卡尔曼滤波对一个连续的状态进行估计,蒙特卡洛定位方法得把世界分割成离散的小块。
- 卡尔曼滤波返回单峰分布结果,蒙特卡洛定位方法返回多峰分布结果。
- 都是定位追踪的方法,粒子滤波是连续多峰
卡尔曼滤波器的输入数据来源于(激光)测距仪,以检测其他车辆包括自行车和行人在多个时刻的位置,预测未来的位置和速度。
高斯函数
卡尔曼滤波的分布以高斯函数给出,它是连续函数,下方面积加起来等于1,特征在于两个参数 平均值μ和称为方差宽度σ 2,在一维参数空间中的任何高斯均以(μ,σ2)表示。
我们的任务是保持一个对未知物体位置最佳估计的μ和σ2。高斯函数完整表达式:
 (lg)
(lg)
编程返回(10,4,8)参数的高斯函数值,并且想办法修改x使得到最大值
from math import * def f(mu, sigma2, x): return 1/sqrt(2. * pi * sigma2) * exp(.5 * (x mu) ** 2 / sigma2) print f(10., 4., 8.) 使x与相同使得后面的表达式为0,lg指数为1便可的最大值
测量和运动
卡尔曼滤波在两个过程中循环:测量值更新和运动值更新。
与定位相同,先测量值然后移动,这里是最大值移动,但原理基本相同,在定位中测量值使用乘法得到,用到了贝叶斯定理;运动值通过卷积得到,用到了全概率定理。
测量循环通常称为测量更新,而运动循环通常称为预测值。 测量更新将使用贝叶斯定理,就是一个乘法。 预测值将使用全概率定理,就是一个卷积,或者简单的一个加法。使用高斯函数来实现这两个步骤:
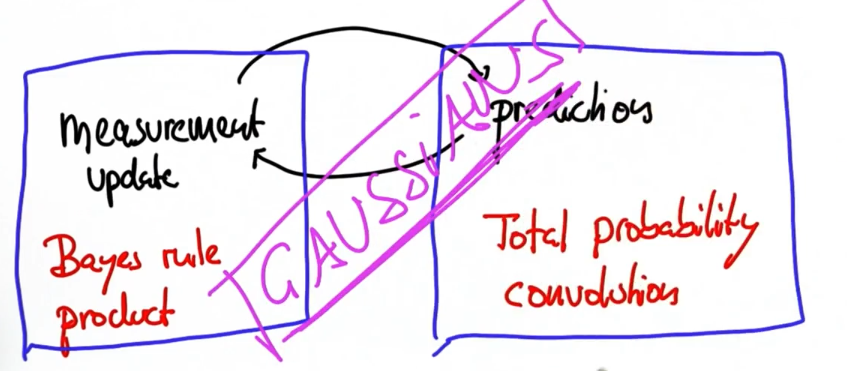
预测的峰值
假设正在定位另一辆车,并且有一个先验mu,函数平滑宽阔(表示不大确定位置),又有一个测量结果值为nu。
现在,高斯函数的新平均值会在哪?它的高度呢?
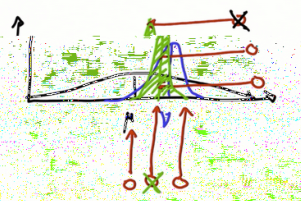
mu与nu之间更靠近nu,因为nu可信度更高,函数越尖可信度越高。
作为结果的高度要高于它的组成部分。
参数更新
假设将两个高斯函数相乘像贝叶斯定理那样,一个先验概率,一个测量值的概率,写出新的平均值和协方差式子(讲义已证明),并从数理上证明新函数位置的确如上。
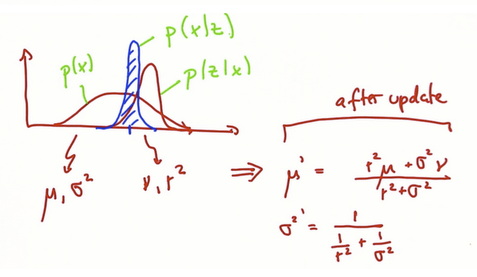
证明是将两高斯函数的指数部分相乘,之后求一阶导令x为0得到新平均值,再二阶导得到新协方差
如果先验和测量的高斯函数是分离的,且宽度相同,新的高斯函数平均值会在哪,高度又如何?
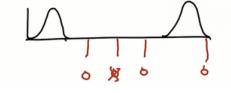

新mu会在两函数中间,且高于组成部分
python化,根据已有两个高斯函数,返回新的平均值和协方差,并以(10., 8., 13., 2.)作为输入求输出
def update(mean2, var1, mean2, var2): new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2) new_var = 1/ (1/ var1 + 1/ var2) return [new_mean, new_var} print update(10., 8., 13., 2.)
>>>12.4, 1.6
预测值(运动循环)
假设一个一维世界,有你对所在位置的最佳估计(x上的蓝色刻度)和你的误差(高斯函数)。 假设向右移动(绿线),动作本身包含自己的误差。 因为运动会丢失信息,得到一个将运动量加到均值上的位置预测,误差比之前增加了。运动的高斯分布平均值U(移动步数)和误差r2(运动的误差),预测结果的高斯分布只是两者加起来。
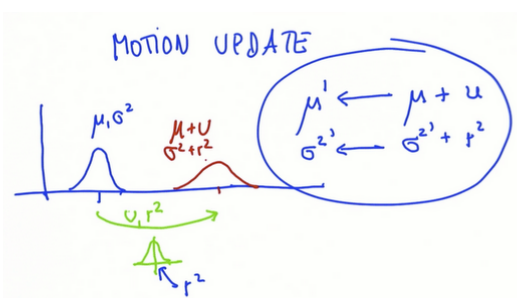
写一个预测函数计算新的更新的均值和方差,使用给定的值获得结果
1 def update(mean2, var1, mean2, var2): 2 new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2) 3 new_var = 1/ (1/ var1 + 1/ var2) 4 return [new_mean, new_var] 5 def predict(mean1, var1, mean2, var2): 6 new_mean = mean1 + mean2 7 new_var = var1 + var2 8 return [new_mean, new_var] 9 print predict(10., 4., 12., 4.)
>>>[22.0,8.0]
这个程序实现了一维卡尔曼滤波器
编写一个主程序,其具有两个函数,更新和预测,根据初始的mu、sigma以及给定的测量和移动的sigma、mu列表,返回新的[mu,sig]对,实现迭代更新。
def update(mean1, var1, mean2, var2): new_mean = float(var2 * mean1 + var1 * mean2) / (var1 + var2) new_var = 1./(1./var1 + 1./var2) return [new_mean, new_var] def predict(mean1, var1, mean2, var2): new_mean = mean1 + mean2 new_var = var1 + var2 return [new_mean, new_var] measurements = [5., 6., 7., 9., 10.] motion = [1., 1., 2., 1., 1.] measurement_sig = 4. motion_sig = 2. mu = 0. sig = 10000. for n in range(len(measurement)): [mu,sig] = updata(mu,sig,measurement[n],measurement_sig) print 'updata: ',[mu,sig] [mu,sig] = pridict(mu,sig,motion[n],motion_sig) print 'predict: ',[mu,sig] print [mu, sig]
代码意义:对于每个测量值重复这两个步骤,即更新和测量,在更新步骤中将新的测量值和以前的预测结合起来产生新的预测(比以前的预测更确信)。在预测步骤中,使用推断出的速度再次创造出一个新的预测(没有以前的预测确信)。
卡尔曼过滤器神奇之处:从来不用担心事情超过两件,更新步骤中是以前的步骤和测量,预测中是以前的预测和推断的速度。这就保持了卡尔曼滤波器所需计算能力较低,并且能实时运行。
多维卡尔曼滤波器假设在一个二维空间中,有一个带有雷达预测每一时刻位置的汽车, 假设t = 0时刻,你的观察对象处于特定的坐标。 稍后又会在其他坐标。t=3可以预测。

在多维空间(如现实世界中)卡尔曼滤波器不仅允许估计你的位置,还要从这些位置测量中推断你的速度。这些推断的速度又可以预测你的未来位置。
注意,传感器本身只能看到位置,不知实际速度,速度从看到的多个位置推断。
具有计算对象速度能力卡尔曼滤波器可以对包含速度的未来位置进行预测。 这就是卡尔曼滤波器在人工智能中如此受欢迎的原因。
高维
已经讨论了一维运动,尽管这捕捉到卡尔曼滤波器的所有要素,但至少应该简要讨论当从一个维度走向更高的维度时会发生什么。
- 平均值成为一个向量, 而不是一个数字,每个维度都有一个元素。
- 方差由协方差代替,当空间具有d维时,它是具有d行和d列的矩阵。
以下是多维高斯的图例,平均值由x 0和y 0表示,协方差是轮廓线:

建立二维预测,其中x轴是位置,y轴是速度,我们将表示为v,位置x相对于时间t的一阶导数是速度的另一种表现。
假设从(1,0)开始,速度变为1,那么下一个预测点会是红点处
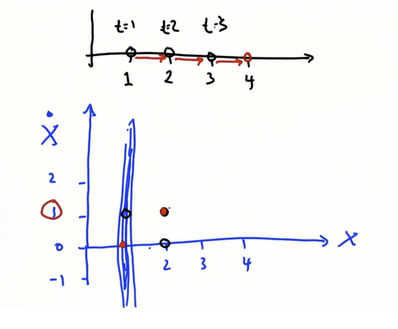
当找到多个数据点时,会发现在一维高斯(蓝色)上的所有可能性都链接到二维高斯(红色)。
先验(红色高斯)和测量(绿色高斯)相乘,以获得对物体速度和位置更好的预测。做数学计算时,会发现在x和y方向都有一个高峰分布,便可以很高的确定性知道我们的位置和速度。多维度高斯相乘的数学尝试查资料。
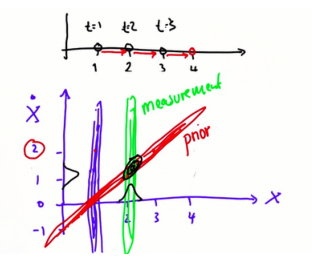
新位置的预测 x'仅仅是以前以前位置的信念x和运动u相加:x'=x+u
卡尔曼滤波器的变量通常被称为“状态”,因为它们反映物理世界的状态,如物体在何处以及移动的速度。 在卡尔曼滤波器中有两个子集:
- 可观察的时刻位置
- 从位置中推测出来的速度
当设计卡尔曼滤波器时,需要效率化两件事情,一种状态转换函数和一种测量函数,它们均表示为矩阵。 称之为状态转移矩阵F和测量矩阵H.
卡尔曼滤波器分为两个步骤:更新步骤和预测步骤。 这些步骤的方程和矩阵及变量的名称如下。

x = 最佳预测,x'=新的x
F = 状态转移矩阵
P =协方差
Z = 测量值
中间未说明的都是过程矩阵,直到最后更新的x、p就好
编写一个给定示例的二维卡尔曼滤波器,可以用到一个包含以上所有公式矩阵操作的类
from math import * class matrix: # implements basic operations of a matrix class def __init__(self, value): self.value = value self.dimx = len(value) self.dimy = len(value[0]) if value == [[]]: self.dimx = 0 def zero(self, dimx, dimy): # check if valid dimensions if dimx < 1 or dimy < 1: raise ValueError, "Invalid size of matrix" else: self.dimx = dimx self.dimy = dimy self.value = [[0 for row in range(dimy)] for col in range(dimx)] def identity(self, dim): # check if valid dimension if dim < 1: raise ValueError, "Invalid size of matrix" else: self.dimx = dim self.dimy = dim self.value = [[0 for row in range(dim)] for col in range(dim)] for i in range(dim): self.value[i][i] = 1 def show(self): for i in range(self.dimx): print(self.value[i]) print(' ') def __add__(self, other): # check if correct dimensions if self.dimx != other.dimx or self.dimy != other.dimy: raise ValueError, "Matrices must be of equal dimensions to add" else: # add if correct dimensions res = matrix([[]]) res.zero(self.dimx, self.dimy) for i in range(self.dimx): for j in range(self.dimy): res.value[i][j] = self.value[i][j] + other.value[i][j] return res def __sub__(self, other): # check if correct dimensions if self.dimx != other.dimx or self.dimy != other.dimy: raise ValueError, "Matrices must be of equal dimensions to subtract" else: # subtract if correct dimensions res = matrix([[]]) res.zero(self.dimx, self.dimy) for i in range(self.dimx): for j in range(self.dimy): res.value[i][j] = self.value[i][j] - other.value[i][j] return res def __mul__(self, other): # check if correct dimensions if self.dimy != other.dimx: raise ValueError, "Matrices must be m*n and n*p to multiply" else: # multiply if correct dimensions res = matrix([[]]) res.zero(self.dimx, other.dimy) for i in range(self.dimx): for j in range(other.dimy): for k in range(self.dimy): res.value[i][j] += self.value[i][k] * other.value[k][j] return res def transpose(self): # compute transpose res = matrix([[]]) res.zero(self.dimy, self.dimx) for i in range(self.dimx): for j in range(self.dimy): res.value[j][i] = self.value[i][j] return res # Thanks to Ernesto P. Adorio for use of Cholesky and CholeskyInverse functions def Cholesky(self, ztol=1.0e-5): # Computes the upper triangular Cholesky factorization of # a positive definite matrix. res = matrix([[]]) res.zero(self.dimx, self.dimx) for i in range(self.dimx): S = sum([(res.value[k][i])**2 for k in range(i)]) d = self.value[i][i] - S if abs(d) < ztol: res.value[i][i] = 0.0 else: if d < 0.0: raise ValueError, "Matrix not positive-definite" res.value[i][i] = sqrt(d) for j in range(i+1, self.dimx): S = sum([res.value[k][i] * res.value[k][j] for k in range(self.dimx)]) if abs(S) < ztol: S = 0.0 res.value[i][j] = (self.value[i][j] - S)/res.value[i][i] return res def CholeskyInverse(self): # Computes inverse of matrix given its Cholesky upper Triangular # decomposition of matrix. res = matrix([[]]) res.zero(self.dimx, self.dimx) # Backward step for inverse. for j in reversed(range(self.dimx)): tjj = self.value[j][j] S = sum([self.value[j][k]*res.value[j][k] for k in range(j+1, self.dimx)]) res.value[j][j] = 1.0/tjj**2 - S/tjj for i in reversed(range(j)): res.value[j][i] = res.value[i][j] = -sum([self.value[i][k]*res.value[k][j] for k in range(i+1, self.dimx)])/self.value[i][i] return res def inverse(self): aux = self.Cholesky() res = aux.CholeskyInverse() return res def __repr__(self): return repr(self.value) ######################################## # Implement the filter function below,以下是核心代码 def kalman_filter(x, P): for n in range(len(measurements)): # measurement update
Z = matrix(measurements[n])
y = Z - (H * x)
S = H * P * H.transpose() + R
K = P * H.transpose() * S.inverse()
x = x + (K * y)
P = (I - (K * H)) * P
# prediction
x = (F * x) + u
P = F * P * F.transpose()
return x,P ############################################ ### use the code below to test your filter! ############################################ measurements = [1, 2, 3] x = matrix([[0.], [0.]]) # initial state (location and velocity) P = matrix([[1000., 0.], [0., 1000.]]) # initial uncertainty u = matrix([[0.], [0.]]) # external motion F = matrix([[1., 1.], [0, 1.]]) # next state function H = matrix([[1., 0.]]) # measurement function R = matrix([[1.]]) # measurement uncertainty I = matrix([[1., 0.], [0., 1.]]) # identity matrix print(kalman_filter(x, P)) # output should be: # x: [[3.9996664447958645], [0.9999998335552873]] # P: [[2.3318904241194827, 0.9991676099921091], [0.9991676099921067, 0.49950058263974184]]
这段代码不算琐事! 它是Google自动驾驶中跟踪其他车辆的核心。 这是以前所见过的逐行实现,测量更新和预测。首先,测量更新n。 误差计算(y = Z(H * x)),矩阵S,卡尔曼增益K与逆,然后回到下一个预测x和测量更新P。最后,用已有方程式完成预测步骤。
对于Google自驾车,这是预测其他车辆的位置以及速度的必要模型。 汽车在前保险杠上使用雷达来测量与其他车辆的距离,并且还会对速度进行估计。 此外,汽车使用其位于屋顶的激光器来测量与其他车辆的距离,并获得速度估计。因此,当Google车辆在路上时,它使用雷达和激光器来估计道路上其他车辆的距离和速度,卡尔曼滤波器使用来自雷达的序列数据,并使用相对距离的状态空间 ,x和y,以及x和y的相对速度,得到状态转换矩阵。
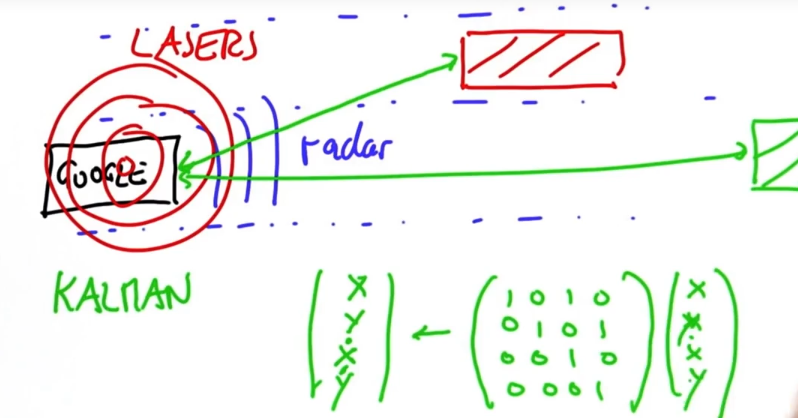
U是动作,可是动作在F中已经包含,那么U的作用到底是什么?
这里讨论的只是追踪目标,并不是控制目标,所以式子里的U设为0,如果可以控制目标可以通过U来设置他的动作
R矩阵的出处在哪里,实际中怎么取得?
噪音矩阵,表示传感器的信号中噪音有多少,目前没有足够理论支持,N.G和S.T有过合作论文《如何学习噪音矩阵》
激光和雷达的测量结果是相同还是不同的,怎样在卡尔曼滤波中使用两个信号源的测量结果?
雷达可以用多普勒效应测量物体速度,这两适合测量不同的物体,在某种程度上是互补的,借助贝叶斯法则可以依次使用这两种传感器的测量结果,对于激光和雷达只用取他们测量结果的乘积。
斯坦利和朱丽尔软硬件上的区别?
斯坦利有6个嵌入式处理器,朱尼尔有2个四核心工控机集成度更高,硬件上最大不同是传感器,斯坦利有廉价的激光测距仪为主安装在正前方,安装有雷达但并未经常使用,朱尼尔安装有更多距离传感器套件,能检测所有方向,被成为周边传感它的激光测距仪安装在顶部旋转。