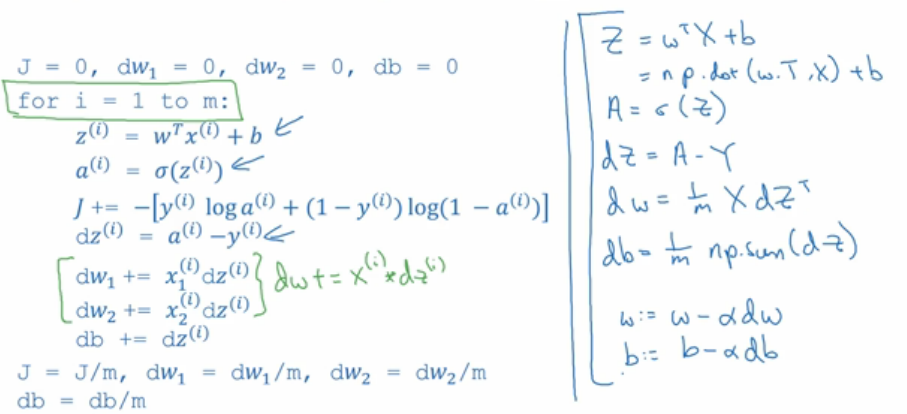二分类问题
在二分分类问题中,目标是训练出一个分类器,这里以图片特征向量x作为输入,预测输出的结果标签y是1还是0,也就是预测图片中是否有猫。 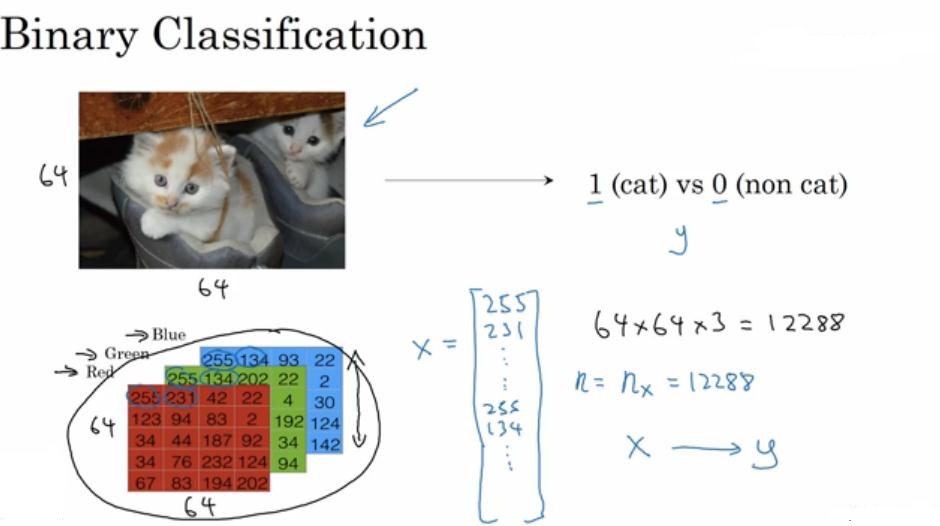
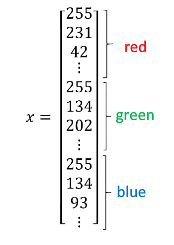
计算机保存一张图片(彩色),要保存三个独立矩阵,分别对应红绿蓝三个颜色通道,如果输入图片是64×64像素,就有三个64×64像素矩阵对应图片中红绿蓝三种像素的亮度。
把这些像素取出来放入特征向量,维度是64×64×3=12288。

- x表示的是特征向量,一个特征向量的长度是nx
- (x,y)表示一个单独样本
- .shape指令是python中的求矩阵维度指令
逻辑回归、梯度下降法
计算图
使用流程图计算函数J(正向传播)

使用流程图计算函数J的导数(反向传播)
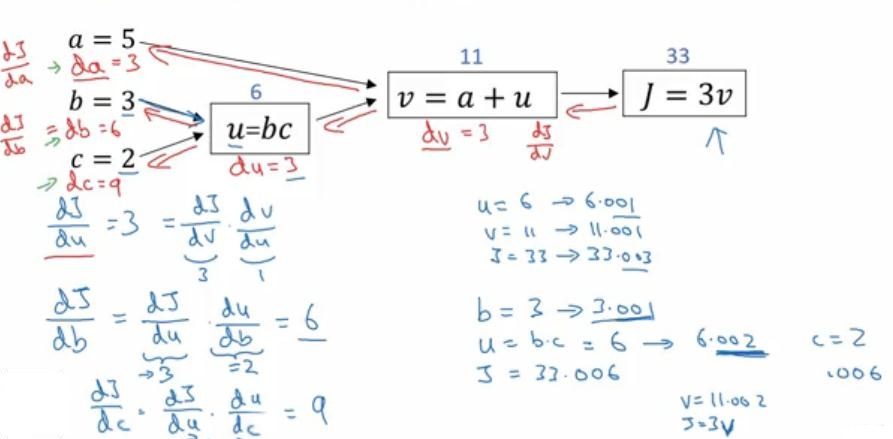
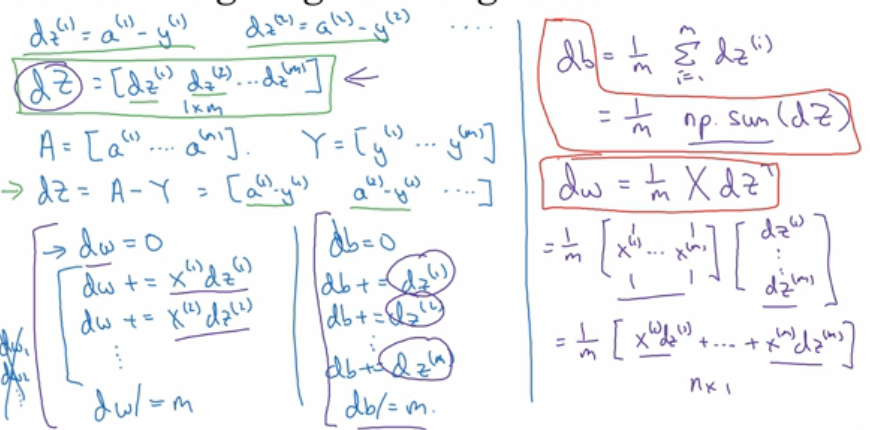
使用导数流程图计算逻辑回归的梯度下降
从后向前算出每一步的导数(偏导)

m个样本的同时梯度下降
梯度下降程序化:
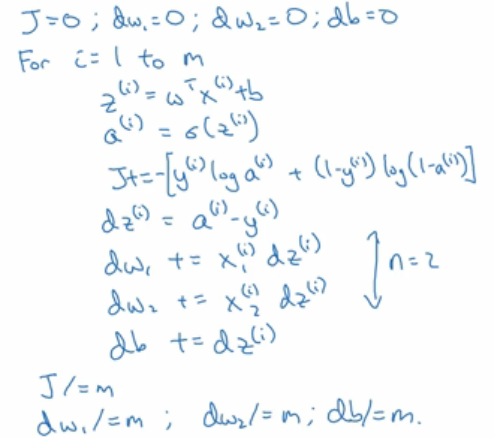
向量化
CPU和GPU都有并行化指令,有时候会叫做SIMD指令(单指令多数据),如果使用了这样的内置函数,比如np.function或者其他能去掉显示for的函数,这样Python的numpy能够充分利用并行化更快地计算,这点对于CPU与GPU上面的计算都是成立的
经验法则:向量化能够消除代码中的for循环,加速算法,只要有其他可能,就不要使用显示for循环
u=AV的向量化非向量化对比
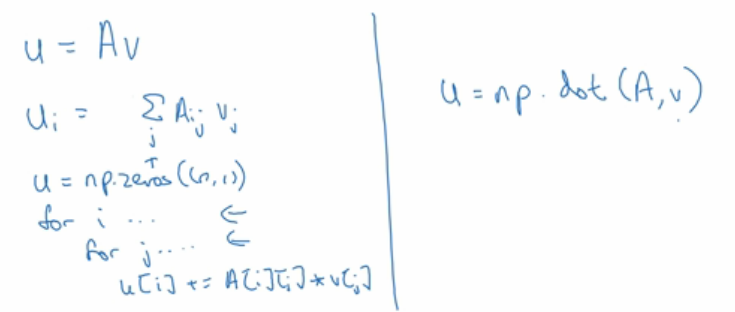
for循环和向量化内置函数对比
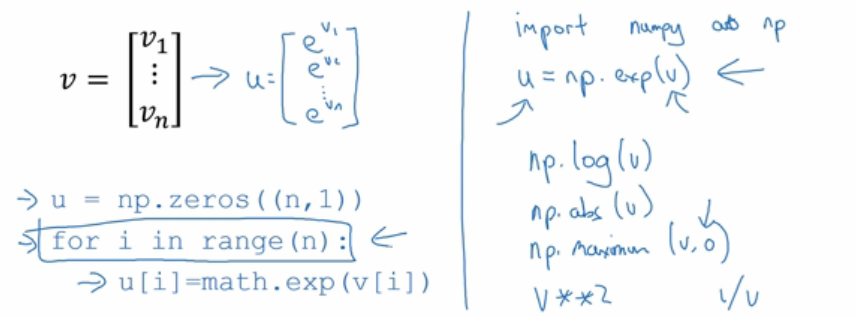
1.用向量化简化一个for,利用的是将循环处理的数据变成向量,再由内置函数批量一次性处理

2.向量化逻辑回归(向量化z和a)
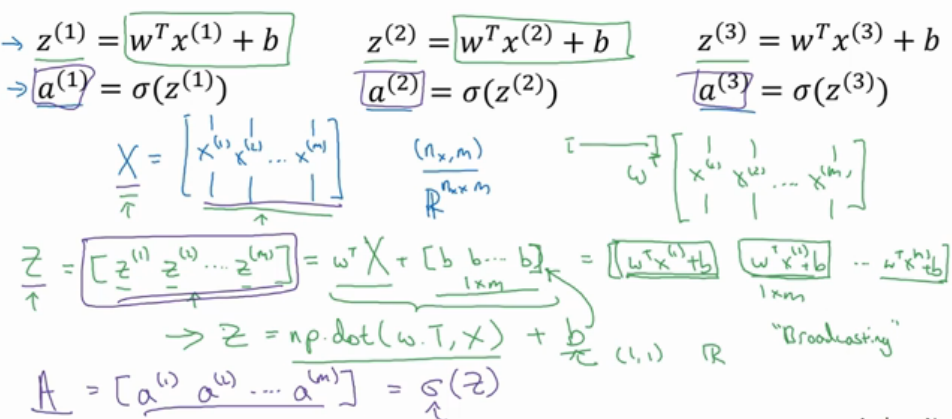
这样只需一行代码就能计算大写Z,大写Z是一个1*m的矩阵,包含所有小写z;
sigmoid函数能处理一个向量,就能把Z当做变量输入,高效地输出大写A
在python中一个向量加上一个实数,会自动把实数扩展成一个向量,这种操作叫做广播,不仅如此,两个不同维度的矩阵相加结果的维度与第一个相同
2.向量化同时计算m个训练数据的梯度
向量化从后向前算出每一步的导数(偏导),并以此简化另一个for循环