原文:https://www.cnblogs.com/lihaichao/p/9627405.html
一.模。
模是指一个计量系统的计数范围。如时钟等。计算机也是一个计算器,它也是有一个计量范围,即都存在一个“模”。
如时钟的计量范围是0~11,模 = 12。
32位计算机的计量范围是2^32,模 = 2^32。
二.补数。
假设当前时针指向11点,而准确时间是8点,调整时间可有以下两种拨法:
- 一种是倒拨3小时,即:
11-3=8 - 另一种是顺拨9小时:
11+9=12+8=8
在以模为12的系统中,加9和减3效果是一样的,因此凡是减3运算,都可以用加9来代替。对“模”12而言,9和3互为补数(二者相加等于模)。所以我们可以得出一个结论,即在有模的计量系统中,减一个数等于加上它的补数,从而实现将减法运算转化为加法运算的目的。
在补码中,0有唯一的表示。
三.补码原理。
# 按以上理论,减一个数等于加上它的补数,所以 5 - 3 # 等价于 5 + (16 - 3) // 算术运算单元将减法转化为加法 # 用二进制表示则为: 0101 + (10000 - 0011) # 等价于 0101 + ((1 + 1111) - 0011) # 等价于 0101 + (1 + (1111 - 0011)) # 等价于 0101 + (1 + 1100) // 括号内是3(0011)的反码+1,正是补码的定义 # 等价于 0101 + 1101 # 所以从这里可以得到 -3 = 1101 # 即 `-3` 在计算机中的二进制表示为 `1101`,正是“ -3 的正值 3(`0011`)的补码(`1101`)”。 # 最后一步 0101 + 1101 等于 1001
四.移码。
移码常用来表示浮点数的阶码。IEEE754中解码用移码表示。

其中X为真值,与补码相比,数值位完全相同,符号位相反。
五.浮点数据表示。

阶码部分E采用的是移码。
为什么采用移码?
原文:https://blog.csdn.net/a7515780/article/details/60469155
单精度浮点数(32位),阶码(后面的用偏移阶码表示,其实在IEEE754表示单精度浮点数都是一个概念)8位,那么原来8位二进制数有符号二进制表示范围是-127~127,但是IEEE为了不在阶码中引入符号位,且8位偏移阶码(阶码中二进制数为无符号数)范围是1~254(为什么不包括0和255?后面说),因此引入偏移码(移码),在有符号位的二进制基础上加127,那么就有了偏移阶码范围0~254,但是0不合法,后面说,因此偏移阶码范围是1~254。 为什么是127呢??是不是很多人都有这个疑惑。 加上127不就从原来的二进制有符号转变为无符号了嘛。IEEE不就是为了不在阶码E中不引入符号位才加的127嘛。
填坑,为什么范围是1~254?
因为0用8位阶码用全0表示,255用8位阶码用全1。 出现全0,尾数M全0,符号位为0,为正0,符号位为1,为负0(IEEE754规定的浮点数有正0负0之分),偏移阶码出现全1,尾数M全0,符号位S为0,为正无穷大,符号位S为1,为负无穷大。 这就是为什么不把0和255放入偏移阶码范围中的原因。
即:全尾数全0或全1时表示其他特殊意义的数。
我之前也在纠结这个问题,纠结在为什么是127不是128或者其他数,其实很简单,就是为了将有符号转换为无符号。 希望我这篇微博可以帮到还处于迷茫的小伙伴。
而移码是真值加一个偏移值得到的。
- 对于单精度而言。偏移值由上得到为:2^7 - 1= 127.
- 对于双精度而言。偏移值由上得到为:2^10 -1 = 1023
所以一个浮点数可表示为:

不同情况:

六.十进制浮点数真值转换为单精度IEEE754.

七.单精度IEEE754转换为十进制浮点数真值.
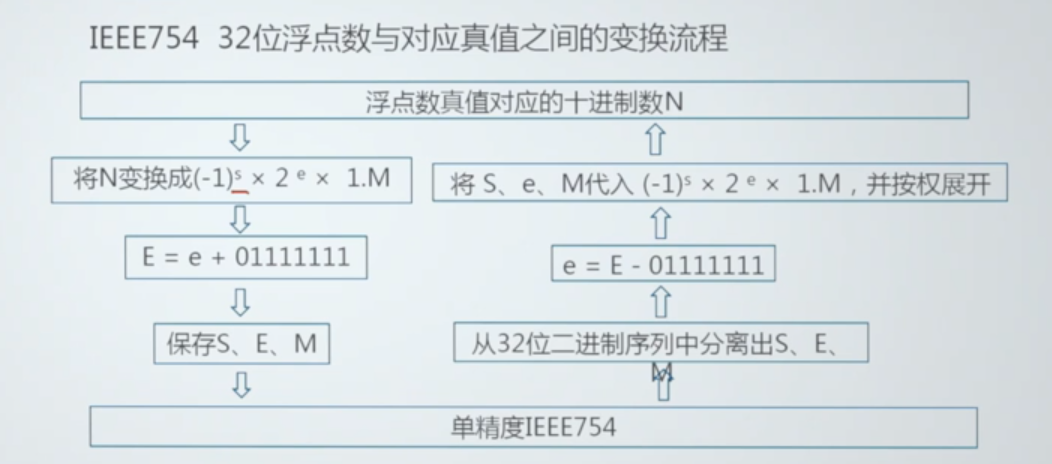
例子:
