示波器测各种类型信号需要多大采样率实测
我们知道示波器的运作过程大致如下图所示:
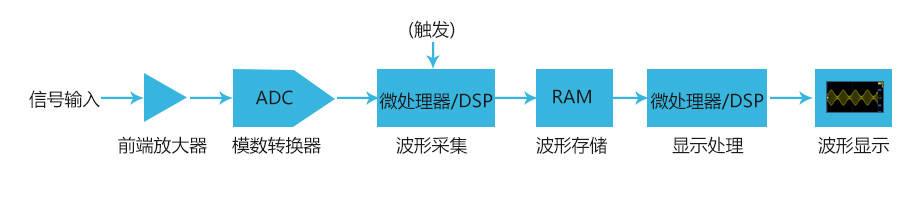
我们通过探头给示波器输入一个信号,被测信号经过示波器前端的放大、衰减等信号调理电路后,然后高速 ADC 模数转换器进行信号采样和数字量化,示波器的采样率就是对输入信号进行模数转换时采样时钟的频率,通俗的讲就是采样间隔,每个采样间隔采集一个采样点。比如 1GSa/s 的采样率,代表示波器具备每秒钟采集 10 亿个采样点的能力,此时其采样间隔就是 1 纳秒。
对于实时示波器来说,目前普遍采用的是实时采样方式。所谓实时采样,就是对被测的波形信号进行等间隔的一次连续的高速采样,然后根据这些连续采样的样点重构或恢复波形。在实时采样过程中,很关键的一点是要保证示波器的采样率要比被测信号的变化快很多。
那么究竟要快多少呢?数字信号处理中的奈奎斯特(Nyquist)定律说, 如果被测信号带宽是有限的,那么在对信号进行采样和量化时,如果采样率是被测信号带宽的 2 倍以上,就可以完全重建或恢复出信号中承载的信息而不会产生混叠。
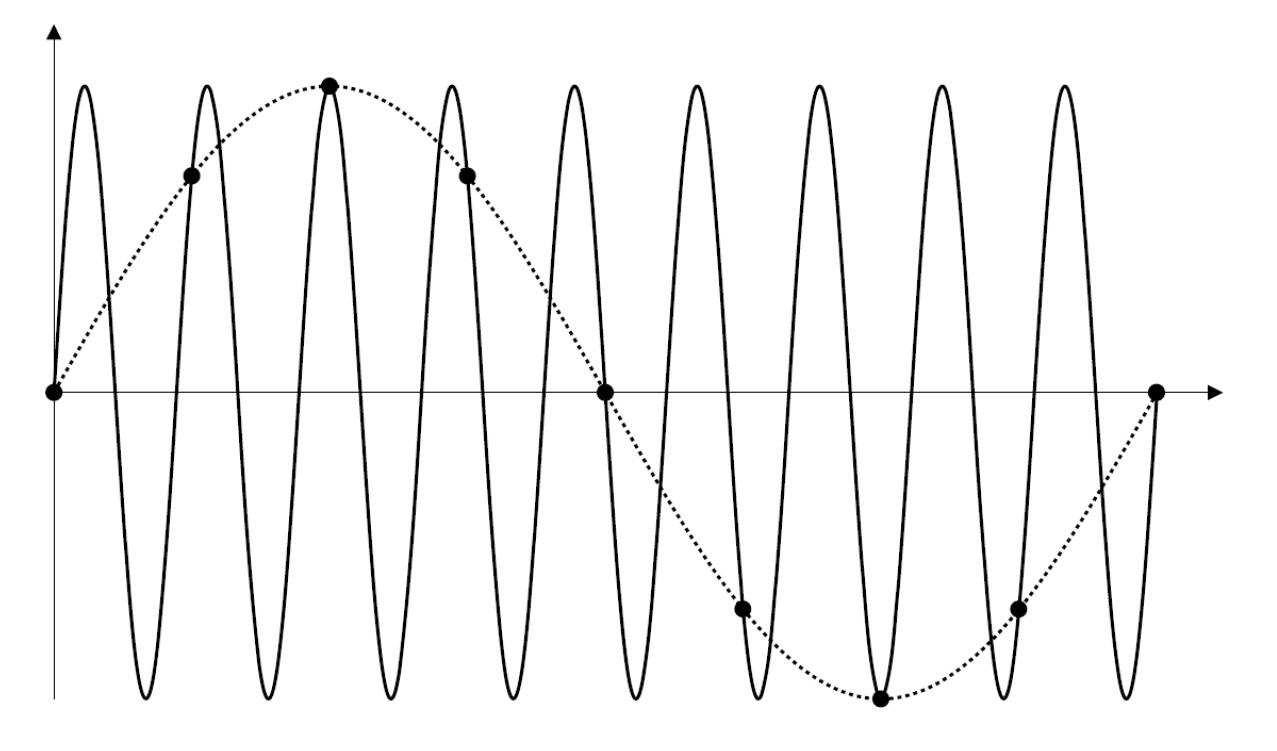
如下图就是采样率不足导致的信号混叠,可以看到采集到的信号和原始信号相比,频率变小了很多。
如果对示波器采样率概念不是很了解的朋友,可以搜索查看我们之前的文章《示波器的采样率概念详解》进行学习。今天我们抛开理论,分别用示波器对 1MHz 正弦波,1MHz 方波,100KHz 锯齿波,100KHz 三角波进行实际测量一下,看看结果。
我们先用信号发生器生成一个幅值为 10V,频率为 1MHz 的正弦波输入到示波器,通过调节存储深度和时基,将采样率降到我们期望的值。如下图种可以看出示波器此时的时基是 2ms,存储深度是 28K,采样率 = 存储深度 /(时基 * 14),采样率正好就是 1MSa/s。
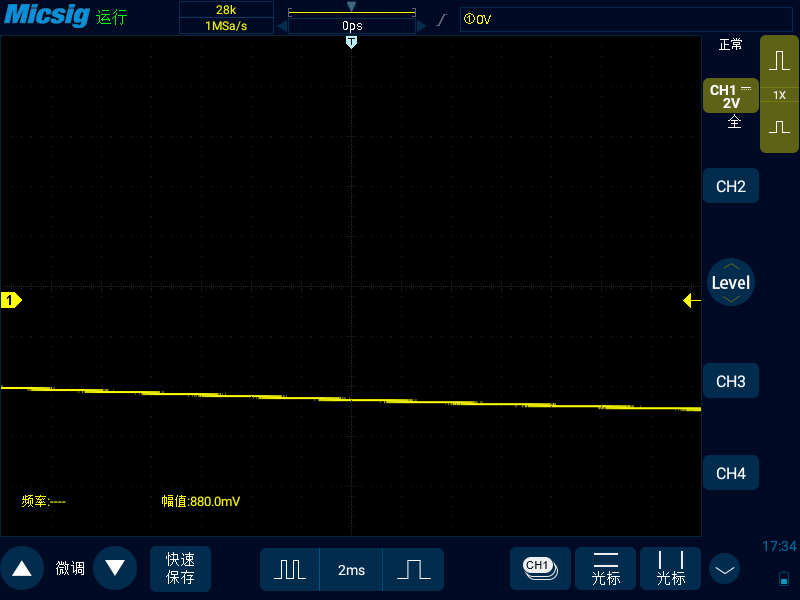
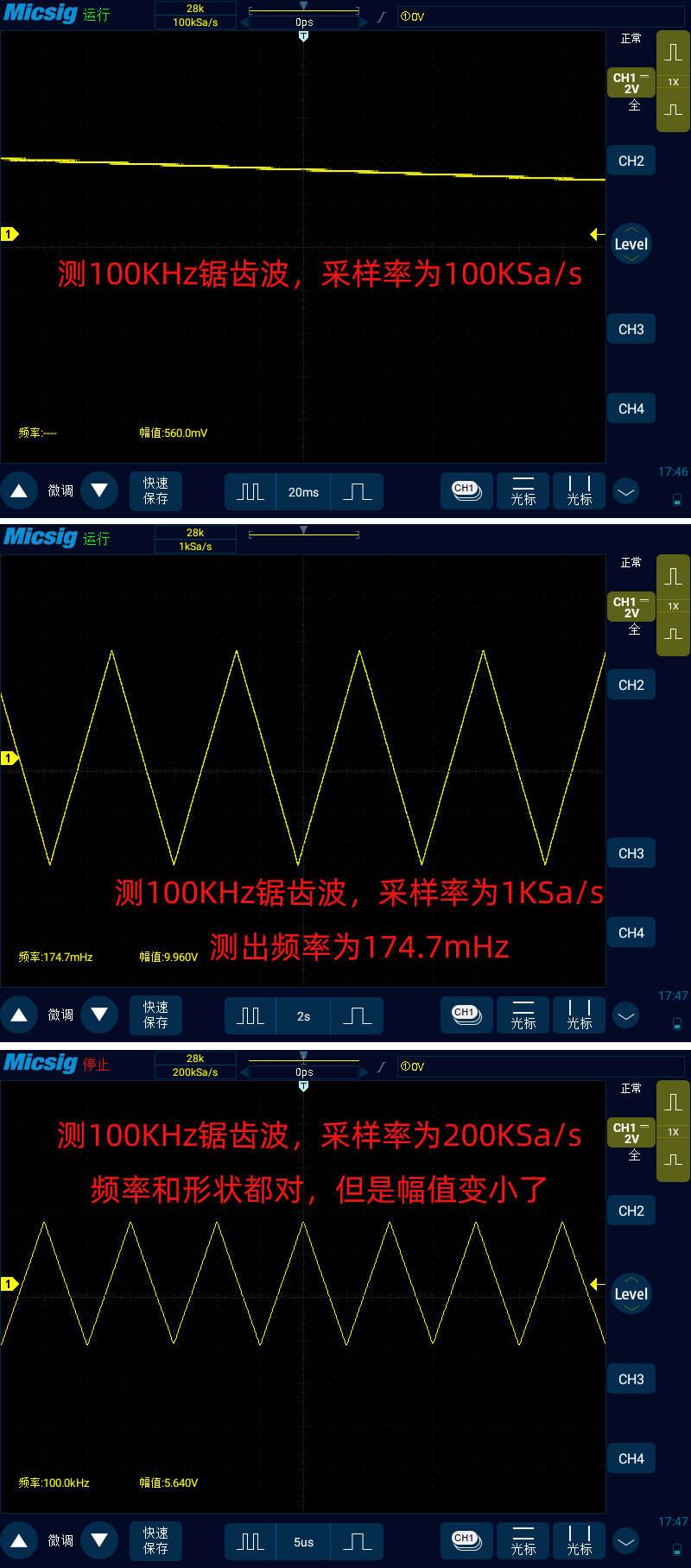
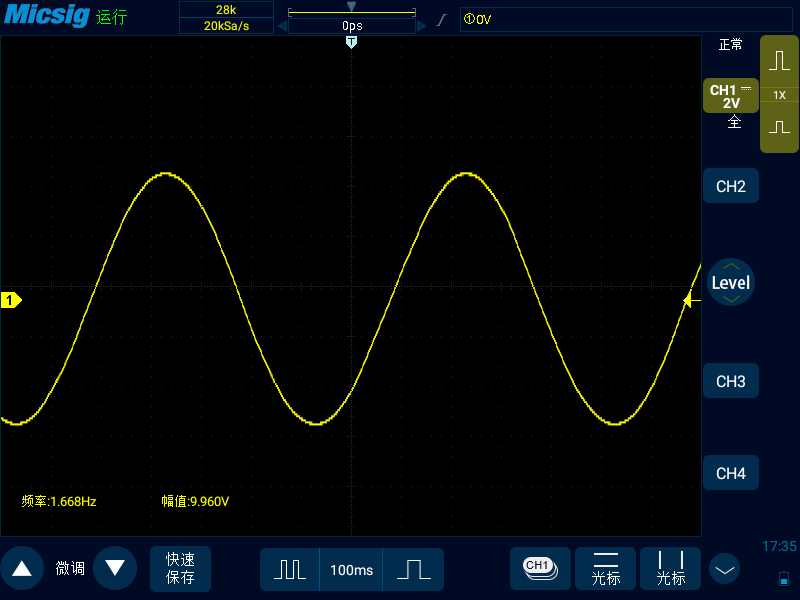
可以看到,当采样率等于信号频率的时候,示波器无法显示正常的正弦波图形,波形已经失真。我们将时基继续打大,存储深度固定不变,此时采样率下降到了 20KSa/s,可以看到示波器屏幕中可以看出信号是正弦波,但是信号的频率从真实的 1MHz 下降到了 1.668Hz,也就是发生了上述采样率不足导致的信号混叠。
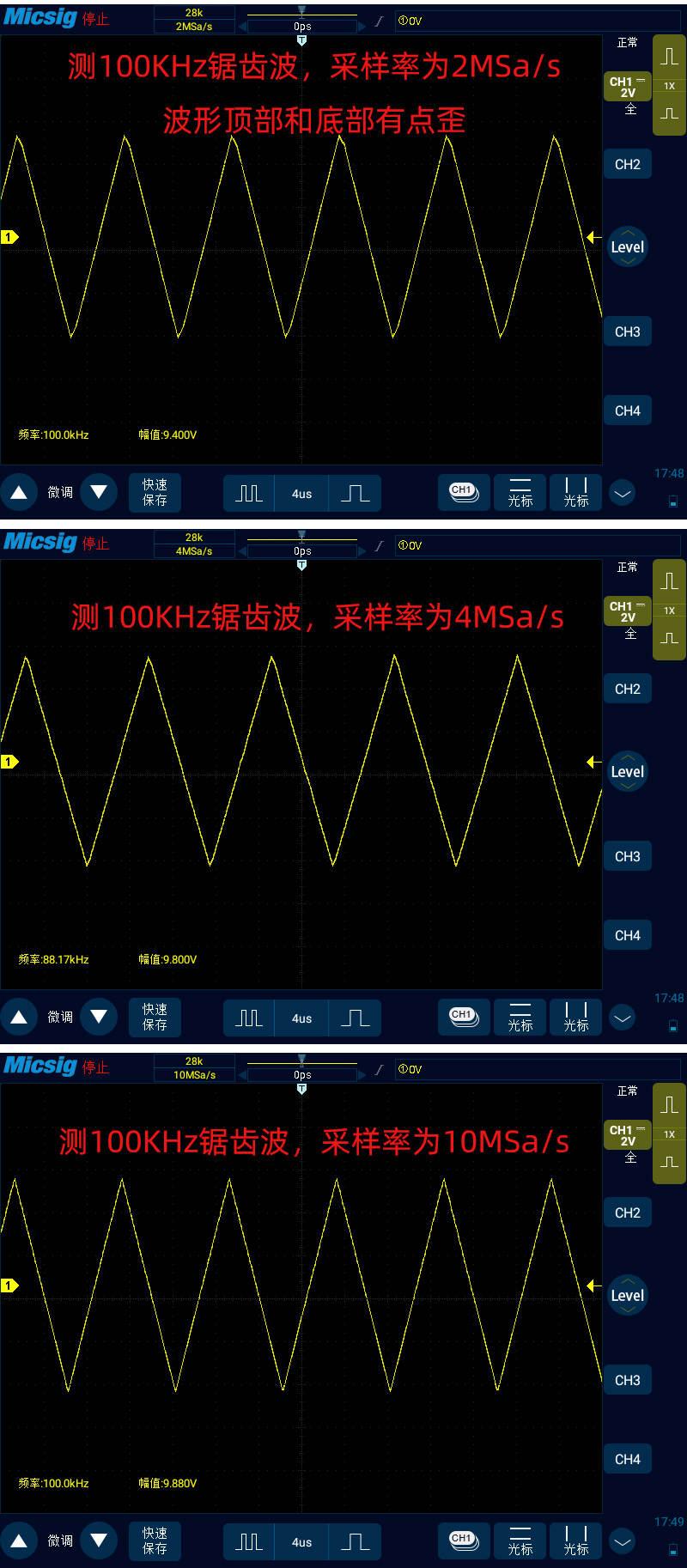
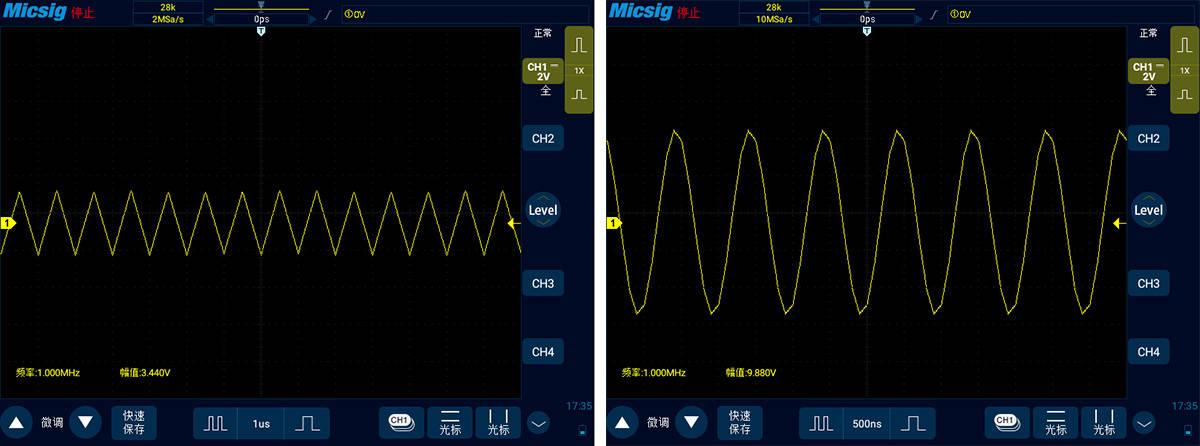
接下去我们将时基调小,这样采样率就变大了,一直调到采样率为信号频率的 2 倍和 10 倍来观察信号变化,也就是 2MSa/s 和 10MSa/s。下图中左边的信号就是 2MSa/s 采样率下的,可以看到信号的频率变回了 1MHz,也就是信号正确的频率值。但是原本的正弦波变成了三角波,波形已经失真。当采样率变为 10MSa/s 时,也就是下图右边的信号,可以看到信号越来越接近正弦波的样子了,但依然不是很漂亮。
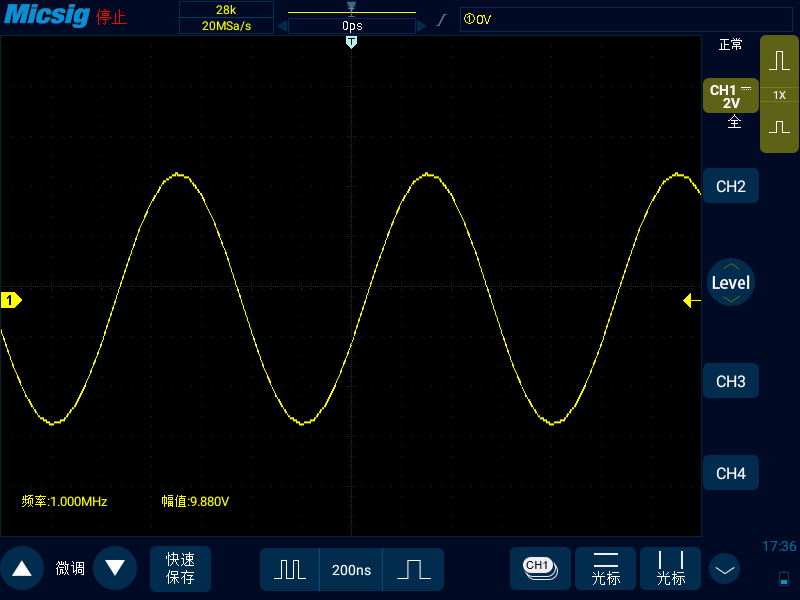
我们继续减少时基,使得采样率为信号频率的 20 倍,也就是 20MSa/s,此时可以看到就是比较漂亮的正弦波了,因此可以得出结论,观察 1MHz 的正弦波,采样率最好可以至少达到其 20 倍,才可以还原信号真实的样子。
我们以同样的方式对 1MHz 方波,100KHz 三角波,100KHz 锯齿波进行实际测量,结果如下图所示:
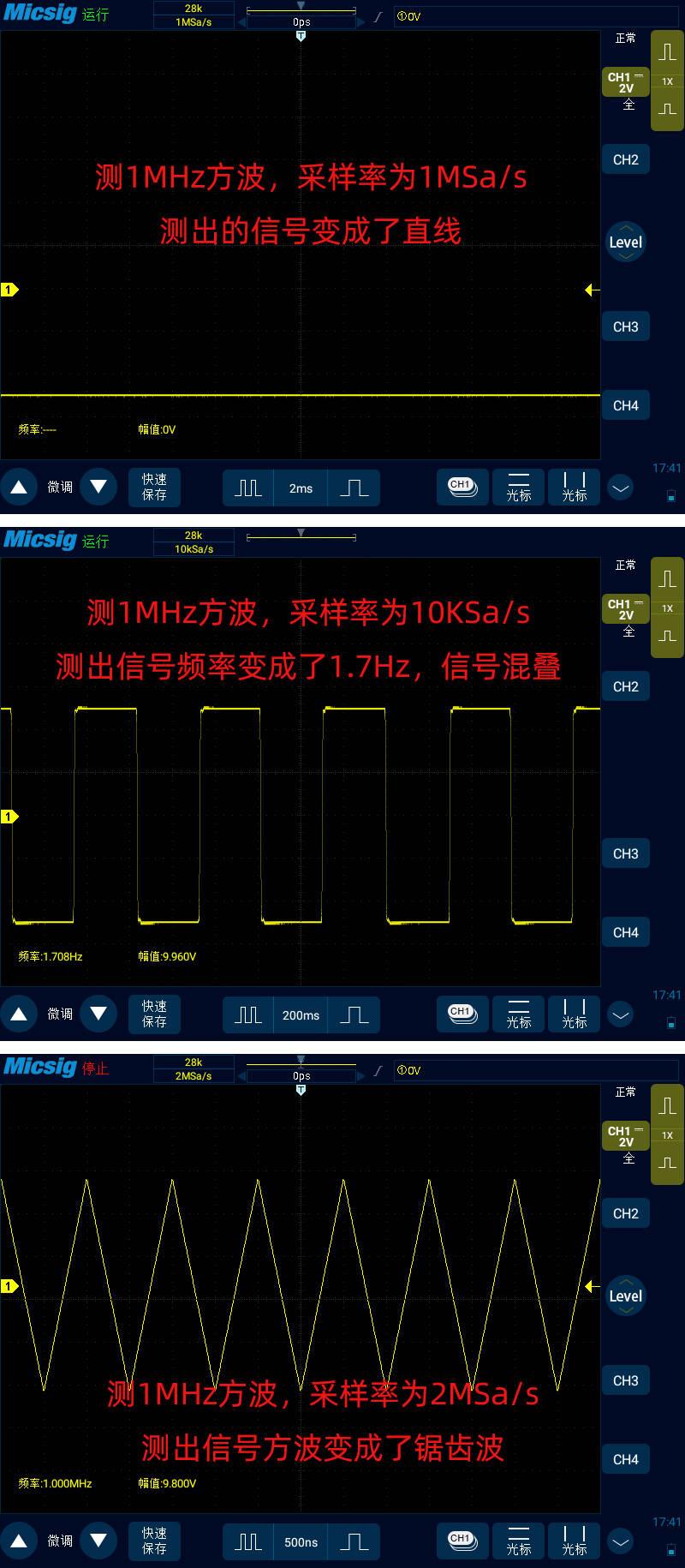
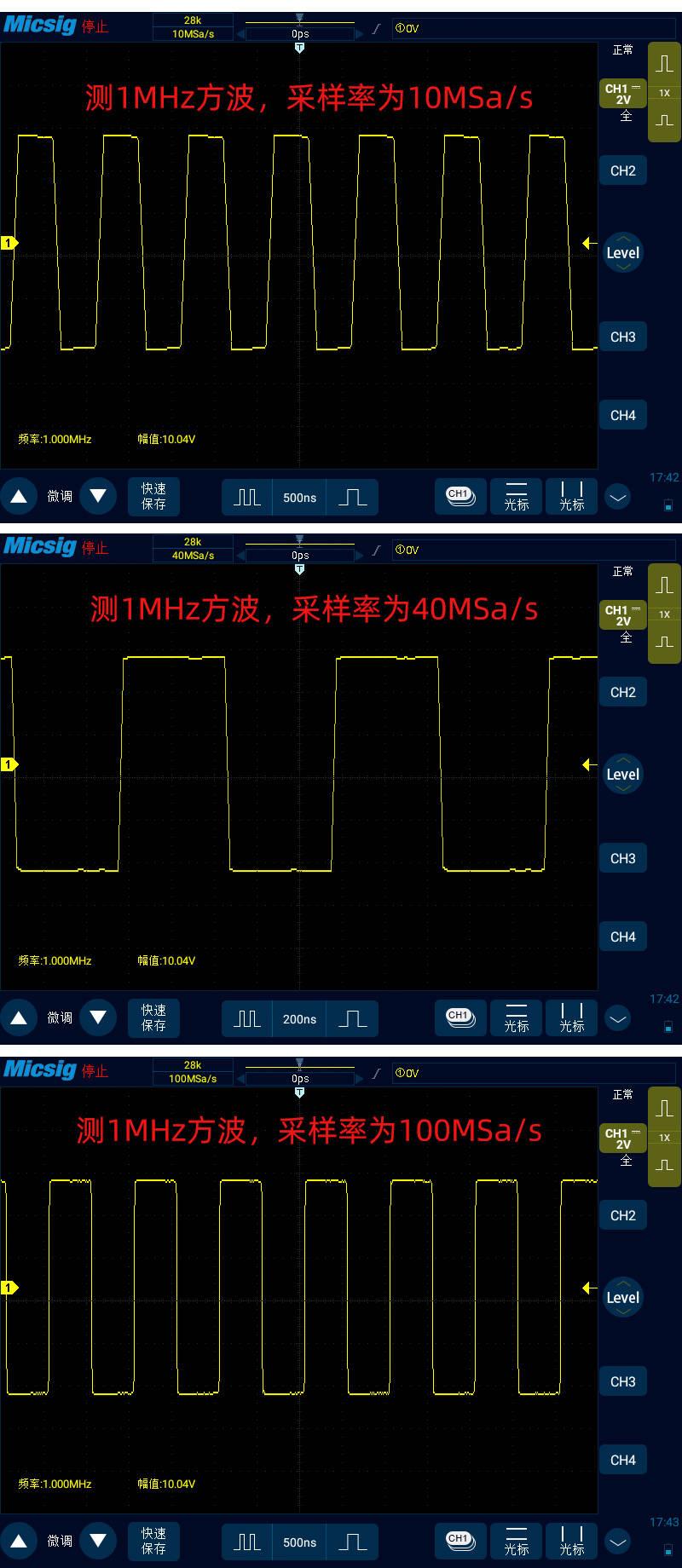
由此可以看出,测量 1MHz 方波对采样率的要求比测量 1MHz 正弦波要高的多。测量 1MHz 正弦波在 20 倍的采样率下就可以接近真实信号,而测量 1MHz 方波即使到了 40 倍上升沿依然坡度比较明显的不直。
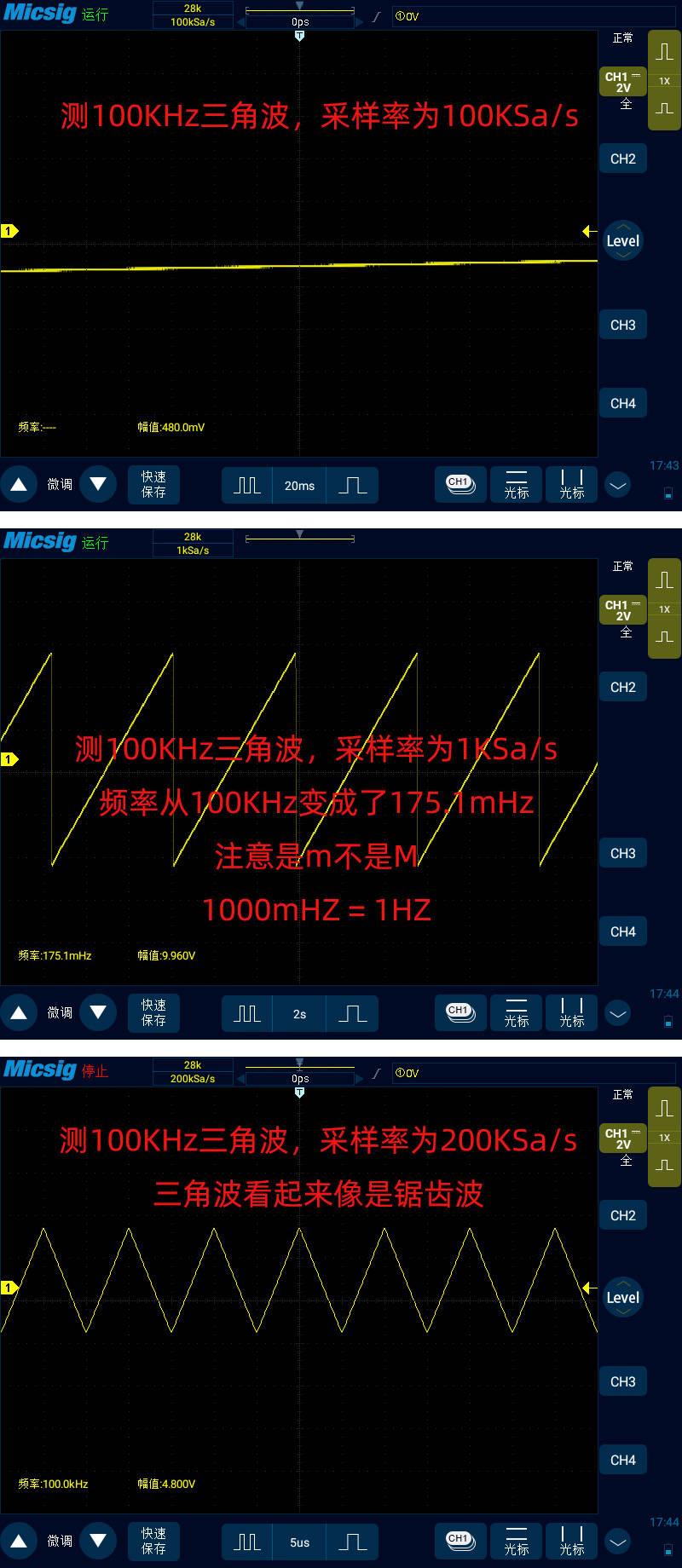
下面来看 100KHz 三角波:

最后我们来看下 100KHz 锯齿波: