多项式全家桶——Part.2 多项式位运算

此划水文全为结论、板子，证明还得看大爷证明。

我们可以用FFT、NTT计算多项式乘法：

[C(k)=sum_{i+j=k}A(i)*B(j) ]

但是计算不了这种玩意：

[C(k)=sum_{i|j=k}A(i)*B(j) ]

或者这种东东：

[C(k)=sum_{i&j=k}A(i)*B(j) ]

或者这种：

[C(k)=sum_{i xor j=k}A(i)*B(j) ]

所以一个算法应着时代的需求诞生了：

多项式位运算

前言

(WTF) FWT是一个神奇的算法，它的名字叫做“快速沃尔什变换”。
虽然不知道百度百科写的是smg，但是网上博客已经足够多以至于让人学懂了。
话说我以前还不知不解地打过这个板子。现在学感觉当时浪费了这么好的一个算法。

或运算

过程

多项式或运算是用来快速做这条式子的：

[C(i)=sum_{i=k|j}A(j)*B(k) ]

其具体思想其实和FFT差不多，首先先把多项式A转化为点值表达，然后再快速运算。
然后再转回插值。这样完成一个算法流程。然鹅我们如何快速DFT这个丑陋的式子呢？
拿出流程图：

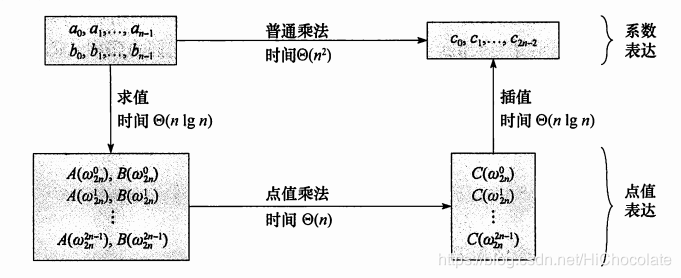
一样三部曲：

如何找出类似于FFT的点值乘法

我们这里并不考虑去什么点值插值，我们只需要一些简单的数论变换即可得到我们所要求的东东。
同样的思路，考虑把A转化成另外一个东东，假设叫做(FWT(A))，其满足可以快速求出(FWT(C)=FWT(A)*FWT(B))。算出来之后还可以快速转化回(A)，也就是(IFWT)逆变换。

首先我们观察柿子：(i|j=k)，我们发现，由于是或运算，看到或运算就应该拆位（这个套路真的好用）。
那么拆完位就可以得到一个结论：如果将k拆位完后，得到1位置集合。那么i的1位置集合与j的1位置集合即为k的1位置集合的子集。
得到这个结论后，我们即可构造：

[FWT(A)=sum_{i=i|j}A(j) ]

这条柿子的意义即为：j的1的位置集合为i的1的位置集合的子集。
（其实为什么这样构造，理由是要去进行一波反演得到的。这里就8推了，记结论）
那么如果把(FWT(A))和(FWT(B))乘起来会变成什么呢？

[FWT(A)*FWT(B)=sum_{i=i|j}A(j)*sum_{i=i|k}B(k)\=sum_{i=i|j}sum_{i=i|k}A(j)*B(k)\=sum_{i=i|(j|k)}A(j)*B(k)\=FWT(C) ]

那么就有方向了。如果现在已经得到一个新的东东(FWT(A))，那么答案就可以在(O(n))时间内求出。
问题是如何快速求出(FWT(A))。

如何找出FWT正变换

同样考虑像FFT一样分治求之。

那么递归可能会慢。怎么办？能不能像FFT一样把下标取出掘其规律？
那就试试。（逝世）

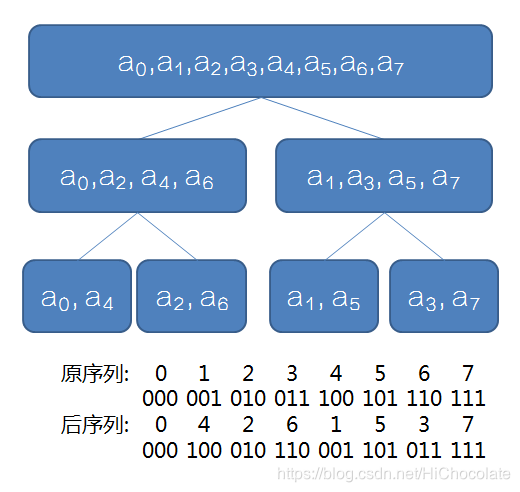
还记得这张神图把。
考虑设a0表示当前分治到的当前位为0的序列，a1表示当前分治到的当前位为1的序列。
再回顾(FWT(A))的定义：

[FWT(A)=sum_{i=i|j}A(j) ]

那么可以知道在对应位置的a0永远是a1的子集。
所以可以写成这个式子：

[FWT(A)=(FWT(A0),FWT(A1+A0)) ]

其中(A1+A0)表示对应位置相加。

于是我们的FWT正变换就完成了。

如何找出FWT逆变换（IFWT）

这个直接理解还挺简单的。我们发现，由于FWT是求子集和，现在要求的是当前值。
所以把子集减去即可。
于是写成这个式子：

[FWT(A)=(FWT(A0),FWT(A1-A0)) ]

后话
话说其实FWT可以有多种方法来看。
网上有的说这其实是FMT（快速莫比乌斯变换）（其实这玩意我真的没搞懂它和反演有什么区别），我一开始看Vfleaking的反演觉得是个子集反演用分治来做。
然鹅比较简单的理解就是从位运算的意义上理解，可以推柿子来比较严谨地去证明，当然也可以我这样直接理解地去推结论。
一个问题有多种角度去看，有时是一件好事，有时却是一件坏事，因为可能会莫衷一是，一开始学会陷入理解的困境。
不管怎样，还是挺好玩的。就好像3blue1brown让我学会的一个道理，去发现数学的美，而不是去死板地认为这个就是一个工具。
诶我tm怎么莫名其妙就放了怎么多没用的屁话

结论

[FWT(A)=(FWT(A0),FWT(A1+A0)) ]

[IFWT(A)=(IFWT(A0),IFWT(A1-A0)) ]

代码

void orfwt(int a[],int inv)
{
	long long op,oq;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				op=inv*a[k];
				oq=a[k+mid];
				op=(op+oq+mo)%mo;
				a[k+mid]=op;
			}
		}
	}
}

和运算

过程

这个过程和或运算的过程其实长得基本一样，就不再推一遍了。

结论

[FWT(A)=(FWT(A0+A1),FWT(A1)) ]

[IFWT(A)=(IFWT(A0-A1),IFWT(A1)) ]

代码

void andfwt(int a[],int inv)
{
	long long op,oq;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				op=a[k];
				oq=inv*a[k+mid];
				op=(op+oq+mo)%mo;
				a[k]=op;
			}
		}
	}
}

异或运算

过程

这个其实和上面的思路差不多，但是构造的东东还是很不同的。

如何找出类似于FFT的点值乘法

考虑设一个函数(f(x))表示当前(x)在二进制表示下1的数量的奇偶性。
则有：

[FWT(A)=sum_{f(i&j)=0}A(j)-sum_{f(i&j)=1}A(j) ]

这玩意当然满足(FWT(C)=FWT(A)*FWT(B))
理由就是把这条柿子带进去，然后再瞎换一下即可得到。
当然，在推柿子的时候可能要用到一个结论：(f(i&j) xor f(i&k)=f(i&(j xor k)))
这里8推了。

如何找出FWT正变换
考虑如何求(FWT(A))
观察柿子：

[FWT(A)=sum_{f(i&j)=0}A(j)-sum_{f(i&j)=1}A(j) ]

由于是位运算，那么继续套路，拆位。
考虑当前第i位，这一位就有4种情况：

• 0 xor 0=0，奇偶性不会改变。
• 0 xor 1=1，奇偶性不会改变。
• 1 xor 0=1，奇偶性不会改变。
• 1 xor 1=0，这时奇偶性改变。

这意味着什么呢？
假如把(FWT(A))取个绝对值（当然这样计算最后的答案是不会改变的），那么就可以把奇偶性改变都看做是减去贡献，反之则为加上贡献。

那么正变换就得到了：

[FWT(A)=(FWT(A0+A1),FWT(A0-A1)) ]

如何找出FWT逆变换（IFWT）

逆变换一样简单，把上面的计算贡献反过来即可。

[IFWT(A)=(frac{IFWT(A0+A1)}2,frac{IFWT(A0-A1)}2) ]

结论

[FWT(A)=(FWT(A0+A1),FWT(A0-A1)) ]

[IFWT(A)=(frac{IFWT(A0+A1)}2,frac{IFWT(A0-A1)}2) ]

代码

void xorfwt(int a[],int inv)
{
	long long op,oq,kk;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				if (inv==1)
				{
					op=a[k];
					oq=a[k+mid];
					kk=(op+oq+mo)%mo;a[k]=kk;
					kk=(op-oq+mo)%mo;a[k+mid]=kk;
				}
				else
				{
					op=a[k];
					oq=a[k+mid];
					kk=(op+oq+mo)%mo*inv2%mo;a[k]=kk;
					kk=(op-oq+mo)%mo*inv2%mo;a[k+mid]=kk;
				}
			}
		}
	}
}

总代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
const long long mo=998244353;
const long long inv2=499122177;

int n,m,a[131072],b[131072],ja[131072],jb[131072];

void orfwt(int a[],int inv)
{
	long long op,oq;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				op=inv*a[k];
				oq=a[k+mid];
				op=(op+oq+mo)%mo;
				a[k+mid]=op;
			}
		}
	}
}

void andfwt(int a[],int inv)
{
	long long op,oq;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				op=a[k];
				oq=inv*a[k+mid];
				op=(op+oq+mo)%mo;
				a[k]=op;
			}
		}
	}
}

void xorfwt(int a[],int inv)
{
	long long op,oq,kk;
	for (int len=2;len<=m;len<<=1)
	{
		int mid=len/2;
		for (int j=0;j<mid;j++)
		{
			for (int k=j;k<m;k+=len)
			{
				if (inv==1)
				{
					op=a[k];
					oq=a[k+mid];
					kk=(op+oq+mo)%mo;a[k]=kk;
					kk=(op-oq+mo)%mo;a[k+mid]=kk;
				}
				else
				{
					op=a[k];
					oq=a[k+mid];
					kk=(op+oq+mo)%mo*inv2%mo;a[k]=kk;
					kk=(op-oq+mo)%mo*inv2%mo;a[k+mid]=kk;
				}
			}
		}
	}
}

void solve(int a[],int b[],int ki)
{
	if (ki==1) orfwt(a,1),orfwt(b,1);
	else if (ki==2) andfwt(a,1),andfwt(b,1);
	else xorfwt(a,1),xorfwt(b,1);
	long long op,oq;
	for (int i=0;i<m;i++)
	{
		op=a[i];
		oq=b[i];
		op=op*oq%mo;
		a[i]=op;
	}
	if (ki==1) orfwt(a,-1);
	else if (ki==2) andfwt(a,-1);
	else xorfwt(a,-1);
	for (int i=0;i<m;i++)
	{
		printf("%d ",a[i]);
	}
	printf("
");
}

int main()
{
	scanf("%d",&n);
	m=1<<n;
	for (int i=0;i<m;i++)
	{
		scanf("%d",&ja[i]);
	}
	for (int i=0;i<m;i++)
	{
		scanf("%d",&jb[i]);
	}
	for (int i=1;i<=3;i++)
	{
		memcpy(a,ja,sizeof(a));
		memcpy(b,jb,sizeof(b));
		solve(a,b,i);
	}
}

学习资料：
http://oi-wiki.com/math/poly/fwt/
https://blog.csdn.net/zhouyuheng2003/article/details/85950280
https://blog.csdn.net/hzj1054689699/article/details/83340154
https://www.cnblogs.com/cjyyb/p/9065615.html
http://blog.leanote.com/post/rockdu/TX20
https://blog.csdn.net/zhouyuheng2003/article/details/84728063
https://zhuanlan.zhihu.com/p/41867199
https://www.cnblogs.com/wjyyy/p/FWT.html