由来
主席树又称函数式线段树,顾名思义,也就是通过函数来实现的线段树
然而我并不知道什么是函数式线段树,某位大爷说:“主席树与可持久化线段树没有区别”。我们暂且相信他怎么说。
主席树大概是 @fotile96 发明的,名字的由来是由于发明人的名字缩写。“HJT”(笑)或是主席树的近亲(可持久化)presistent≈(主席)president得名的吧。
好了,接下来我们来详细讲讲主席树到底是个啥吧。
定义?不存在的
我也不知道怎么定义。
主席树就是利用函数式编程的思想来使线段树支持询问历史版本、同时充分利用它们之间的共同数据来减少时间和空间消耗的增强版的线段树。
说白了,也就是可持久化线段树。
引入
写博客的大佬都是先从一到例题来引入的对吧?
那么我们也用一个简单的例题来引入。
给你一个n个数的数列a,m次每次询问l~r区间内的第k小数。
很熟悉对吧?
简单做法:对于每次询问,排个序,直接输出。
简单暴力,当然,便宜货除了便宜,其他什么都不好——O(n log n*m)
有点机智的做法:暴力建n颗权值线段树。当然,这个做法机智就机智在可以在线段树上二分来搞。
然而过于机智,我没打过。这个做法随便分析一下你就会发现还是不够优秀。
有个更机智的做法:归并树。顾名思义就是根据归并排序实现的。详细的讲就是每个节点保存的是该区间归并排序后的序列,然后就可以并来并去了。
但是你用脑子想想就会发现虽然比之前的做法机智了些,但还是很慢,空间也很大,所以一般只有无脑的人才会用归并树用在这。
为什么这么说?因为接下来要介绍很有脑子的做法。
那就是最机智的做法:主席树。(可持久化权值线段树)
我们回到之前暴力建权值线段树的机智做法。为了保障时间满足,我们用脑子想想我们可以发现直接用一个前缀和来维护即可。这样一来我们的时间可以稍微保证一下,但是我们的空间还是很大,怎么办?凉拌
正题
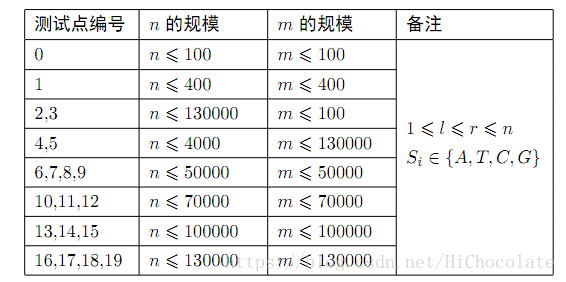
接下来我们用一张图来解释:
这是一颗权值线段树,上面编号表示l~r区间内的信息所在的节点。这个不懂就先去看看权值线段树再来学主席树吧,不然看不懂的。我原来也是这样.jpg
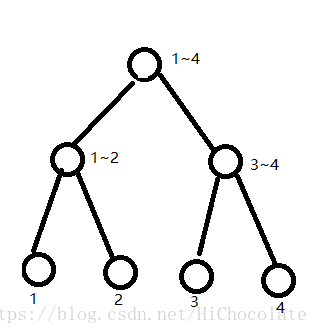
然后我们同样暴力建出n个权值线段树,每个节点表示l~r区间内的数的个数。如下图:

注:每棵树表示1~i(当前树的位置)所有的数字建成的权值线段树的样子。
仔细理解理解。
Q:为什么要这样建
A:就是对于每次询问区间第k小的时候,可以利用前缀和的特性来维护区间第k小。
因为我们当前第r棵树是1~r所有数的权值线段树,于是我们找出的第k小也是1~r区间内的,但是我们可以同时搞第l-1棵树内的比k小的数(或想你怎么弄),然后我们就可以算出l~r区间内的第k小的数了。
这也是要仔细思考思考,研究研究。
然后,我们再等等,请再思考思考,研究研究。
再思考思考,研究研究(重要的事情说三遍)
思考完了吗?往下看:

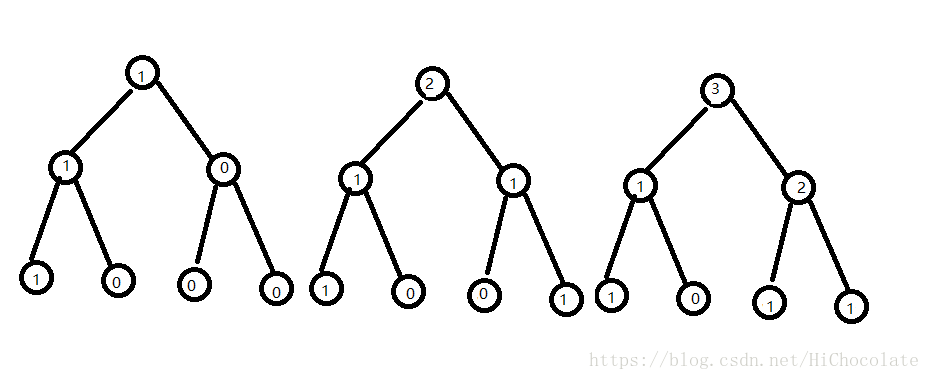
先回忆一下,刚才的做法我们是要优化空间,上面就有一个极为机智的方法。
看到中间的树和左边的树,我们发现左边的树红色圈圈部分是与中间的树一样的。
wow!这个发现很神奇对吧~
然后同样的
右边的树与中间的树也有相同的。
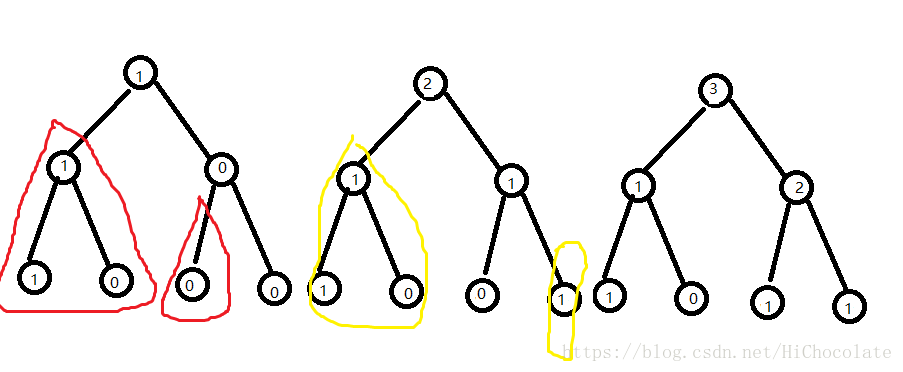
然后我们反过来看,当前的树与之前的树只有一条东东是不同的,也就是一条长为log的链,然后是当前树所对应修改的数的一条链。
看图来理解,效果更佳。
那么,我们就可不可以每颗数只保留一条log的链,其他的不弄出来占空间呢?
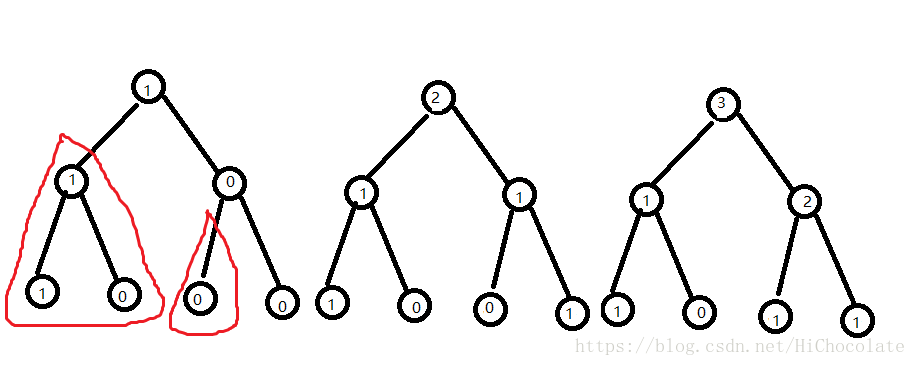
再来看图(相信我,看图理解效果很好)
这个图很神奇地把后面一颗树重复的东东在前面几颗树里面找到了,
并且把它连了一条边,把这一块东东作为了当前树里面的一个子树。
是不是很神奇,很美妙?
别急着赞叹,赶紧理解理解,我们马上就要来谈谈如何运用了。
练习
NO.1
【GDKOI2009模拟3】Zoo from——jzoj1011
Description
JZ拥有一个很大的野生动物园。这个动物园坐落在一个狭长的山谷内,这个区域从南到北被划分成N个区域,每个区域都饲养着一头狮子。这些狮子从北到南编号为1,2,3,…,N。每头狮子都有一个觅食能力值Ai,Ai越小觅食能力越强。饲养员西西决定对狮子进行M次投喂,每次投喂都选择一个区间[I,J],从中选取觅食能力值第K强的狮子进行投喂。值得注意的是,西西不愿意对某些区域进行过多的投喂,他认为这样有悖公平。因此西西的投喂区间是互不包含的(即区间[1,10]不会与[3,4]或[5,10]同时存在,但可以与[9,11]或[10,20]一起)。同一区间也只会出现一次。你的任务就是算出每次投喂后,食物被哪头狮子吃掉了。
Input
觅食能力值。(1<=能力值<=maxlongint)。此后M行,每行描述一次投喂。第t+2的三个数I,J,K表示在第t次投喂中,西西选择了区间[I,J]内觅食能力值第K强的狮子进行投喂。
Output
输出文件有M行,每行一个整数。第i行的整数表示在第i次投喂中吃到食物的狮子的觅食能力值。
Sample Input
7 2
1 5 2 6 3 7 4
1 5 3
2 7 1
Sample Output
3
2
Data Constraint
对于100%的数据,有1<=N<=100000,1<=M<=50000。
好吧,也就是区间第k小。
我们很显然地可以建一颗主席树来弄。
怎么弄呢?我们结合代码来看:
procedure insert(l,r,x:longint;var y:longint);
var
mid:longint;
begin
if l=r then
begin
inc(tot);
y:=tot;
size[y]:=size[x]+1;
left[y]:=left[x];
right[y]:=right[x];
end
else
begin
inc(tot);//节点个数
y:=tot;
size[y]:=size[x]+1;//当前节点包含的数字的个数
left[y]:=left[x];//左儿子
right[y]:=right[x];//右儿子
mid:=(l+r) div 2;
if a[i]<=mid then
begin
insert(l,mid,left[x],left[y]);
end
else
begin
insert(mid+1,r,right[x],right[y]);
end;
end;
end;看着很像普通的线段树对吧~~~
然后我们就是查询操作了:
function find(l,r,x,y,kth:longint):longint;
var
mid:longint;
begin
if l=r then
begin
exit(ans[l]);//退出答案
end
else
begin
mid:=(l+r) div 2;//二分的过程
if size[left[y]]-size[left[x]]>=kth then//找找l~r区间内的x~y的个数有多少个。
begin
exit(find(l,mid,left[x],left[y],kth));
end
else
begin
exit(find(mid+1,r,right[x],right[y],kth-size[left[y]]+size[left[x]]));
end;
end;
end;也很简单对吧~
但是对于本题需要注意的一个东东是,他的范围很大,所以我们需要离散化一下。
标程:
uses math;
var
a,b,c,ans,root:array[0..100000]of longint;
size,left,right:array[0..10000000] of longint;
i,j,k,l,n,m,tot,x,y,z,zd:longint;
procedure discretize;
var
i,j,k,l:longint;
procedure qsort(l,r:longint);
var
i,j,k,m:longint;
begin
i:=l;j:=r;
m:=a[(l+r) div 2];
repeat
while a[i]<m do inc(i);
while a[j]>m do dec(j);
if i<=j then
begin
k:=a[i];
a[i]:=a[j];
a[j]:=k;
k:=b[i];
b[i]:=b[j];
b[j]:=k;
inc(i);dec(j);
end;
until i>j;
if l<j then qsort(l,j);
if r>i then qsort(i,r);
end;
begin
fillchar(b,sizeof(b),0);
fillchar(c,sizeof(c),0);
for i:=0 to n do b[i]:=i;
qsort(0,n);
c[b[0]]:=0;
j:=0;
for i:=1 to n do
begin
if (a[i]=a[i-1]) then
begin
c[b[i]]:=c[b[i-1]];
end
else
begin
inc(j);
c[b[i]]:=j;
end;
end;
zd:=0;
j:=0;
for i:=1 to n do
begin
if a[i]<>a[i-1] then
begin
inc(j);
inc(zd);
ans[j]:=a[i];
end;
end;
fillchar(a,sizeof(a),0);
for i:=0 to n do a[i]:=c[i];
end;
function find(l,r,x,y,kth:longint):longint;
var
mid:longint;
begin
if l=r then
begin
exit(ans[l]);
end
else
begin
mid:=(l+r) div 2;
if size[left[y]]-size[left[x]]>=kth then
begin
exit(find(l,mid,left[x],left[y],kth));
end
else
begin
exit(find(mid+1,r,right[x],right[y],kth-size[left[y]]+size[left[x]]));
end;
end;
end;
procedure insert(l,r,x:longint;var y:longint);
var
mid:longint;
begin
if l=r then
begin
inc(tot);
y:=tot;
size[y]:=size[x]+1;
left[y]:=left[x];
right[y]:=right[x];
end
else
begin
inc(tot);
y:=tot;
size[y]:=size[x]+1;
left[y]:=left[x];
right[y]:=right[x];
mid:=(l+r) div 2;
if a[i]<=mid then
begin
insert(l,mid,left[x],left[y]);
end
else
begin
insert(mid+1,r,right[x],right[y]);
end;
end;
end;
begin
assign(input,'zoo.in');reset(input);
assign(output,'zoo.out');rewrite(output);
readln(n,m);
for i:=1 to n do
begin
read(a[i]);
end;
discretize;
for i:=1 to n do
begin
insert(1,zd,root[i-1],root[i]);
end;
for i:=1 to m do
begin
readln(x,y,z);
writeln(find(1,zd,root[x-1],root[y],z));
end;
end.
end.NO.2
【清华集训2014】mex from——jzoj3547
Description
有一个长度为n的数组{a1,a2,…,an}。m次询问,每次询问一个区间内最小没有出现过的自然数。
Input
第一行n,m。
第二行为n个数。
从第三行开始,每行一个询问l,r。
Output
一行一个数,表示每个询问的答案。
Sample Input
5 5
2 1 0 2 1
3 3
2 3
2 4
1 2
3 5
Sample Output
1
2
3
0
3
Data Constraint
对于30%的数据:
1<=n,m<=1000
对于100%的数据:
1<=n,m<=200000
0<=ai<=10^9
1<=l<=r<=n
偷偷告诉你,这题可以离线搞。
但是在线可以用主席树来弄,我们就来看看:
NO.2.5
【北大夏令营2018模拟5.13】Mex from——jzoj5710
描述根上题一样,只是多加了个强制在线而已。
那么我们就来看这道题。
本题就是让我们求一个区间内最小的没有出现的数字。
那么我们也可以同样地建一颗权值线段树,但是我们这棵树记录的是当前区间内的值出现的min(最右位置)
然后一个二分(从R开始),如果区间内所有数的最右位置都≥L以内就在右边,否则在左边
是不是很神奇?主席树博大精深!
代码:
uses math;
var
a,b,c,ans,root:array[0..200000]of longint;
left,right,tree:array[0..4000000] of longint;
i,j,k,l,r,n,m,tot,x,y,z,zd,mid,answer:longint;
function find(x,l,r,kth:longint):longint;
var
mid:longint;
begin
if l=r then
begin
exit(l);
end
else
begin
mid:=(l+r) div 2;
if tree[left[x]]<kth then
begin
exit(find(left[x],l,mid,kth));
end
else
begin
exit(find(right[x],mid+1,r,kth));
end;
end;
end;
procedure insert(l,r,x:longint;var y:longint);
var
mid:longint;
begin
if l=r then
begin
inc(tot);
y:=tot;
left[y]:=left[x];
right[y]:=right[x];
tree[y]:=i;
end
else
begin
inc(tot);
y:=tot;
left[y]:=left[x];
right[y]:=right[x];
mid:=(l+r) div 2;
if a[i]<=mid then
begin
insert(l,mid,left[x],left[y]);
end
else
begin
insert(mid+1,r,right[x],right[y]);
end;
tree[y]:=min(tree[left[y]],tree[right[y]]);
end;
end;
begin
assign(input,'mex.in');reset(input);
assign(output,'mex.out');rewrite(output);
readln(n,m);
for i:=1 to n do
begin
read(a[i]);
insert(0,200000,root[i-1],root[i]);
end;
for i:=1 to m do
begin
readln(x,y);
writeln(find(root[y],0,200000,x));
end;
end.
end.NO.3
【NOI2016模拟7.16】基因改造计划 from——jzoj4645
Description

Input

Output

Sample Input
6 2
ACACAA
1 3
3 6
Sample Output
4
6
Hint
Data Constraint
10%easy
20%马拉车或回文自动机
30%神奇的DP 我不会
45%~75%莫队 别看我,我不会
对于我这种蒟蒻来看,可以拿的部分分好少,真不够良心的。
直接看100%
这题还需要用到马拉车来做(Manacher)
先学吧~~
学会的看下面:
首先,我们求出半径f[i]
那么就代表有f[i]+1个不同的字符串对吧。
我们对于每次询问,很显然地就发现了——

L=l*2+1
R=r*2+1
然后我们可以求一个mid=(L+R) div 2;
然后呢,我们就把它分为两个部分搞:
for k:=L to mid do
ans:=ans+min(f[k],k-L);
&
for k:=mid+1 to R do
ans:=ans+min(f[k],R-k);
然后呢,我们看第一个部分。
k-L是不定的,我们想把它变成一定的,那么就变成
min(f[k]-k,-L)+k
然后呢,f[k]-k也是可以预处理出来变成一个东东,我们记为pp[k]
第二部分也是一样的。
于是,我们就要去掉min。
通过分类讨论我们可以发现,这就是个可持久化权值线段树——
对于一段区间,我们查询比-L小的数的和,同时我们求出有多少个比-L小的数,然后通过繁琐的计算,我们就可以在log 的时间复杂度内给出每次询问的答案。
当然,也可以看作是经典的求二维矩阵内点权和,当然,我不会。
开玩笑的,其实就是弄弄扫描线,然后再排排序,于是我们就可以很好地离线搞啦~~
由于本文讲的是主席树,于是我们就只看看主席树的做法——
代码:
var
f,pp,pp1,sum,sum1,sum2:array[0..1000000] of int64;
tree1,tree2,size1,size2:array[0..5000000]of int64;
root1,root2,left1,right1,left2,right2:array[0..5000000] of longint;
i,j,k,l,n,m,x,y,o,p,mid,zd1,zd2,zx1,zx2,tot1,tot2,gs,mid1:longint;
s,v:ansistring;
ans:int64;
ch:char;
function min(x,y:longint):longint;
begin
if x<y then exit(x);
exit(y);
end;
function max(x,y:longint):longint;
begin
if x>y then exit(x);
exit(y);
end;
procedure find2(l,r,x,y,kth:longint);
var
mid:longint;
begin
if (l=r) then
begin
ans:=ans+tree2[y]-tree2[x];
gs:=gs+size2[y]-size2[x];
end
else
begin
if l+r<0 then mid:=(l+r-1) div 2
else mid:=(l+r) div 2;
if mid>=kth then
begin
find2(l,mid,left2[x],left2[y],kth);
end
else
begin
find2(mid+1,r,right2[x],right2[y],kth);
ans:=ans+tree2[left2[y]]-tree2[left2[x]];
gs:=gs+size2[left2[y]]-size2[left2[x]];
end;
end;
end;
procedure insert2(l,r,x:longint;var y:longint;value:longint);
var
mid:longint;
begin
if (l=r) then
begin
inc(tot2);
y:=tot2;
size2[y]:=size2[x]+1;
left2[y]:=left2[x];
right2[y]:=right2[x];
tree2[y]:=value*size2[y];
end
else
begin
inc(tot2);
y:=tot2;
size2[y]:=size2[x]+1;
left2[y]:=left2[x];
right2[y]:=right2[x];
if l+r<0 then mid:=(l+r-1) div 2
else mid:=(l+r) div 2;
if value<=mid then
begin
insert2(l,mid,left2[x],left2[y],value);
end
else
begin
insert2(mid+1,r,right2[x],right2[y],value);
end;
tree2[y]:=tree2[y]+tree2[left2[y]]+tree2[right2[y]];
end;
end;
procedure find1(l,r,x,y,kth:longint);
var
mid:longint;
begin
if (l=r) then
begin
ans:=ans+tree1[y]-tree1[x];
gs:=gs+size1[y]-size1[x];
end
else
begin
if l+r<0 then mid:=(l+r-1) div 2
else mid:=(l+r) div 2;
if mid>=kth then
begin
find1(l,mid,left1[x],left1[y],kth);
end
else
begin
find1(mid+1,r,right1[x],right1[y],kth);
ans:=ans+tree1[left1[y]]-tree1[left1[x]];
gs:=gs+size1[left1[y]]-size1[left1[x]];
end;
end;
end;
procedure insert1(l,r,x:longint;var y:longint;value:int64);
var
mid:longint;
begin
if (l=r) then
begin
inc(tot1);
y:=tot1;
size1[y]:=size1[x]+1;
left1[y]:=left1[x];
right1[y]:=right1[x];
tree1[y]:=value*size1[y];
end
else
begin
inc(tot1);
y:=tot1;
size1[y]:=size1[x]+1;
left1[y]:=left1[x];
right1[y]:=right1[x];
if l+r<0 then mid:=(l+r-1) div 2
else mid:=(l+r) div 2;
if value<=mid then
begin
insert1(l,mid,left1[x],left1[y],value);
end
else
begin
insert1(mid+1,r,right1[x],right1[y],value);
end;
tree1[y]:=tree1[y]+tree1[left1[y]]+tree1[right1[y]];
end;
end;
begin
assign(input,'gene.in');reset(input);
assign(output,'gene.out');rewrite(output);
readln(n,m);
s:='~#';
readln(v);
for i:=1 to length(v) do s:=s+v[i]+'#';
s:=s+'`';
l:=length(s);
x:=0;
y:=0;
for i:=2 to l-1 do
begin
if x>i then f[i]:=min(f[2*y-i],x-i) else f[i]:=1;
while s[i+f[i]]=s[i-f[i]] do inc(f[i]);
if f[i]+i>x then
begin
x:=f[i]+i;
y:=i;
end;
end;
for i:=1 to l do
begin
zx1:=min(zx1,f[i]-i-2);
zx2:=min(zx2,f[i]+i-2);
zd1:=max(zd1,f[i]-i-2);
zd2:=max(zd2,f[i]+i-2);
end;
for i:=1 to l do
begin
f[i]:=f[i]-1;
if f[i]>0 then
pp[i]:=f[i]-i-1
else
pp[i]:=zd1+1;
if f[i]>0 then
pp1[i]:=f[i]+i-1
else
pp1[i]:=zd2+1;
if f[i]>0 then sum[i]:=sum[i-1]+i
else sum[i]:=sum[i-1];
if f[i]>0 then sum1[i]:=sum1[i-1]+1
else sum1[i]:=sum1[i-1];
if (f[i]>0) and (f[i] mod 2=0) then sum2[i]:=sum2[i-1]+1
else sum2[i]:=sum2[i-1];
end;
for i:=1 to l do
begin
if i=14 then
j:=0;
insert1(zx1,zd1+1,root1[i-1],root1[i],pp[i]);
insert2(zx2,zd2+1,root2[i-1],root2[i],pp1[i]);
j:=0;
end;
for i:=1 to m do
begin
ans:=0;
read(o,p);
mid:=(o*2+1+p*2+1) div 2;
mid1:=(p+o) div 2;
ans:=0;
gs:=0;
find1(zx1,zd1+1,root1[o*2],root1[mid],-(o*2+1));
ans:=ans+(sum1[mid]-sum1[o*2]-gs)*(-(o*2+1));
ans:=ans+sum[mid]-sum[o*2]+sum2[mid]-sum2[o*2];
gs:=0;
find2(zx2,zd2+1,root2[mid],root2[p*2+1],(p*2+1));
ans:=ans+(sum1[p*2+1]-sum1[mid]-gs)*(p*2+1);
ans:=ans+sum2[p*2+1]-sum2[mid];
ans:=ans-sum[p*2+1]+sum[mid];
ans:=ans div 2;
ans:=ans+p-o+1;
writeln(ans);
end;
end.
end.
温馨提示:有很多很多关于div 2 的计算会导致答案错误,所以这题真的很难很难调。
可以列为比较难的入门题了吧。
结尾的话
还是不存在的。
主席树是个很多用的个东东,他虽然有点难想到,身价很高,比起暴力看很“贵”。但是,贵的东西只有一个缺点,就是贵,其他什么都好。所以比赛拿这这个贵的东东,打更多部分分或是切题乃是很好的一个东东,更重要的是,可以锻炼你的思维,让你多思考多思考,对整个人都是有益的!