#总
费用流+KM算法 √
#费用流(spfa版)
首先费用流是个什么东东呢?
就是最大流的升级版——加了一个费用限制。
什么意思?
最简单的问题——
farmer John要从自来水厂引水来自己家,有n个水中转站,m条水管,水管一次性的,流量为w,那么farmer John要最多的水流到自己家中。
(最大流)
farmer John要从自来水厂引水来自己家,有n个水中转站,m条水管,水管一次性的,流量为w,费用为v,那么farmer John要在有最多的水流到自己家中的情况下,费用最小。
(费用流)
这就是区别。
一个直观的想法——
能不能用最大流的处理方法类似地处理费用流呢??
答案是可以的!
首先,我们用spfa跑一下以费用为权值的最短路,那么就可以贪心地求出最小的费用。
然后我们就在最大流的基础上,将dfs增广换成spfa的最短路。
每次加入最少费用的边,然后流过去,当然,要连反向边。
证明?
大家都会ford-fulkerson(FF)或Edmonds-Karp(EK)吧?
你说不会?
自己学。
那么这种就像上面两种最大流的方法,找一条单位费用最小的路,增广。
然后不行的话可以有反向边,所以不会出现错误。
这样好像是单路增广。
会跑得有点慢,怎么办?
先讲讲两个小优化:
(从网上学的)
1、一个是slf优化,就是对于spfa的进队操作,进之前判一下若小于队头就直接插在队头,这个还是蛮有用的,可以提升点速度;
2、 另一个是记路径的时候可以不用记前趋点,只要记边,反向边指向的就是前趋,就不用多开一个数组的空间。
很神奇?
但是正如作者所说——“提升点速度”
我们雄心勃勃地想要提升很多速度,怎么办?
这个过程就很像dinic。
你又说你不会?我才不会再发张——震惊.jpg给你看呢
过程就像是这样:
首先我们求出spfa,然后用dfs增广。
每次增广完就把路径上的节点清空,然后找增广路上最早的一个有流量的点,然后继续增广。
实现多路增广!
时间提升很多?是的,但是还是不够多!我们要更多!
#KM算法
诶,你刚刚要讲更好的算法,怎么来讲这个带权二分图匹配问题?
因为学好这个,你就可以由更好的思路来搞搞阵。
首先你会不会匈牙利算法?
你又不会?
孺子不可教也。
自己上百度。
那么我们现在学会了匈牙利了。
我们就来看看KM算法是个什么东东。
这个就是求最大匹配费用的。
KM算法大致思路就是求出一个距离编号,然后每次匹配的时候就边匹配,边修改这个距离编号。
具体怎么做可以看看这个blog——
https://www.cnblogs.com/logosG/p/logos.html
十分完整。
至于为什么我不写,是因为这不是主要的要讲的东西。
我们只是需要借助到其中的一个思想。
只与距离编号相同的边匹配,若是找不到边匹配,对此条路径的所有左边顶点-1,右边顶点+1,再进行匹配,若还是匹配不到,重复+1和-1操作。
这个就是重点了。
具体怎么做就看上面的blog,然后我们就借助这个思想来做更强大的费用流。
#zkw费用流
首先,zkw是一位卡常大佬,我们都很清楚他的线段树《统计的力量》
当然,他的费用流也如他的线段树一样好用。
主要思想仍然是找增广路,只是有了一些优化在里边。
原来我们找增广路主要是依靠最短路算法,如SPFA。因此此算法的时间复杂度主要就取决于增广的次数和每次增广的耗费。
由于每一次找增广路是都是重新算一遍,有时会浪费时间。
然后,如何优化时间呢?
运用到上面的KM算法,我们就弄一个距离编号dis[i]表示汇点到源点的最短路。
然后呢,我们每次走就像是KM一样,找一个dis[i]=dis[tov[i]]+map[i,tov[i]]
然后我们就可以这样子来增广。
一旦不存在到达终点的路径,就扫描每一条边,找到最小的距离增加值,使得有至少一条新边被加入相等子图。
这就是核心的东东。
算法流程——
1、计算dis(spfa或dij)
2、从源点开始流,每次流一条流量大于0的边,而且满足上面的式子。流完之后,我们还有连反向边。然后依次寻找,寻找完了之后到3
3、我们就开始考虑更改dis。
扫描每一条边,找到最短距离增加值,然后修改dis值。
如果没有变可以修改了,那么代表算法结束。
否则继续走2。
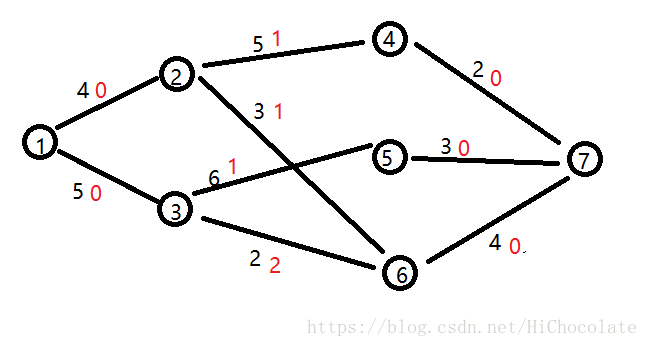
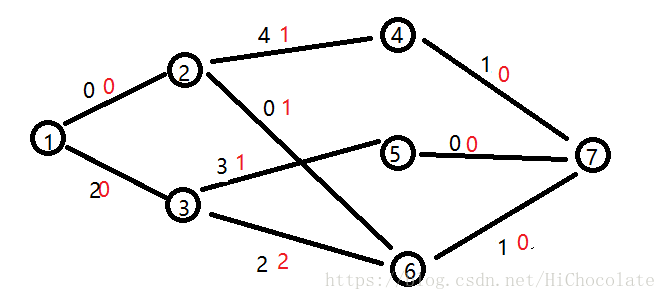
我们来画图模拟模拟(其实很简单)
红色为费用,黑色为流量
然后,我们可以算出:
dis[1,1,1,0,0,0,0]
然后,我们就从1开始流。
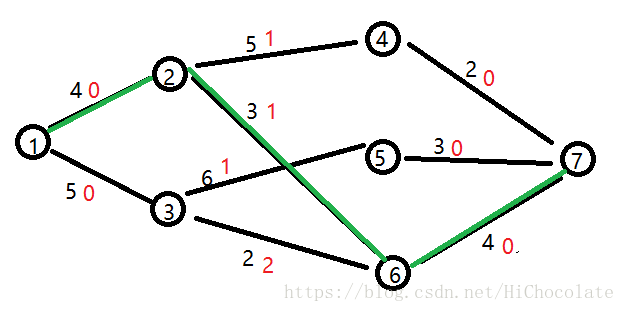
直观的流法——
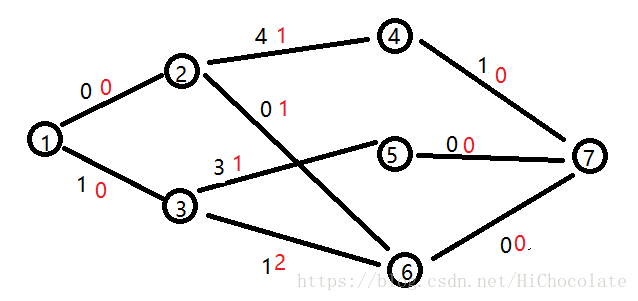
然后流量就变了——
继续流从2→4,然后再到3,到5——
6跑不到,因为dis[3]<>dis[5]+map[3,5]
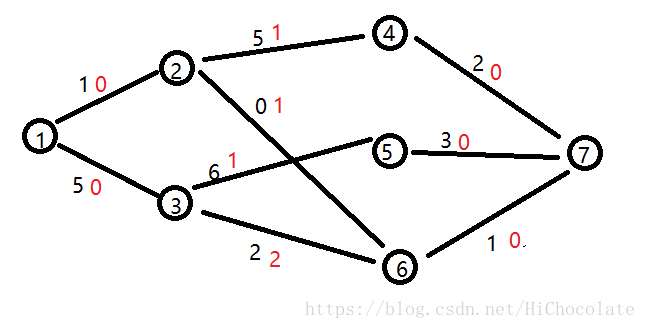
然后,我们就要开始考虑更改dis了。
我们选择一个费用比较小的且流量>0的边,也就是3→5。
那么,我们就更新:
dis[2,1,2,0,0,0,0]
这样就可以流到6了。
但是,我们发现一个蛋疼的东东——
1→3的流量还是1。
这样不是最优。
那么我们就可以考虑反向边了。
那么我们根据最大流的一些证明,最后可以在这个图中流到最大流!
至于怎么流,就很麻烦模拟了,自己手玩吧~~~
记住!
必须要学通最大流的各种算法,然后再来学这个费用流,否则将会很难理解。
我们发现,其实zkw的算法有点像sap。
233
所以说,你还可以加当前弧优化等等。
(我不知道可不可以加GAP)
还可以加动态加边的优化(很好用!!!)
然后你问我负边怎么弄?
这个自己想
我不知道
分析优缺点:
优点:
zkw在重标号的时候,只是对于一个对边操作,比spfa优很多,因为spfa会不止一次地去扫描。
zkw是多路增广的,所以这样可以优化很多路径费用相等的情况。
缺点:
zkw可能会在增广的时候,只增加一个重复标号,然后就可能不能次次增广,那么就会很慢。
所以:
zkw用在费用取值范围不大的图或增广路较少的图很优。
如果相反呢?你还用spfa吗?
不不不,我们可以考虑——
SLF优化。
用SLF优化的spfa来维护zkw的距离编号,那么就可以保留多路增广。
但是,除了第一次以外,spfa都工作在一个所有边均为正数的图上(线性规划),这和不维护顶标记直接spfa不同。
那么我们想想看,spfa甚至可以用dij来做。
这个方法在稠密的二分图上不够优秀,但是远远胜过原来的spfa。而且,在其他图上,这个方法比原来的zkw和spfa更优。
为什么?这个zkw是多路增广,而且使用了线性规划,缩小了费用范围,那么就可以很高效地来针对缺点去优化。而且,线性规划后,更可以使SLF来发挥作用。dij来完成之后的工作,比原来的zkw快的原因是:在流小费用大距离长的图上,一次性把距离标号改对往往比反复调整更有效率。
上述纯属zkw大佬优~~(ka)~~化 ~~(chang)~~神技,我只是负责口胡一下,这个优化的详细请看:
https://artofproblemsolving.com/community/c1368h1020435
一个非zkw的伪代码——
uses math;
var
dis:array[1..10000] of longint;//距离编号
last,next,kp,tov,flew,value,id,now:array[1..10000] of int64;//分别表示路线开始、下一条边、记录原来状态、终点、流量、费用、反向弧编号、当前弧优化。
pd:array[1..102]of boolean;//记录哪些点满足等式,注意,它记录点的访问情况
function flow(x,t:longint):longint;
var
k,l,minn:longint;
begin
pd[x]:=true;//该点被流到,说明满足等式
if x=en then
begin
inc(ans,t*dis[1]);//流到啦,记录答案
exit(t);
end;
k:=now[x];
while k<>0 do
begin
if (flew[k]>0) and (pd[tov[k]]=false) and //判断点是否可以到达
(dis[x]=dis[tov[k]]+value[k])then//判断是否满足等式
begin
minn:=min(t,flew[k]);
l:=flow(tov[k],minn);
if l>0 then
begin
inc(flew[id1[k]],l);//修改流量
dec(flew[k],l);
now[x]:=k;//当前弧优化
exit(l);
end;
end;
k:=next[k];
end;
now[x]:=0;//当前弧优化
exit(0);
end;
function change:boolean;
var
minn,k:longint;
begin
minn:=maxlongint;
for i:=1 to n+m+2 do
begin
if pd[i] then
begin
k:=kp[i];
while k<>0 do
begin
if (flew1[k]>0)and(pd[tov1[k]]=false)and(dis[tov1[k]]+value1[k]-dis[i]<minn)
then minn:=dis[tov1[k]]+value1[k]-dis[i];
k:=next1[k];//寻找费用最小的边
end;
end;
end;
if minn=maxlongint then exit(true);
for i:=1 to n+m+2 do
begin
if pd[i] then
begin
inc(dis[i],minn);//修改距离标号
pd[i]:=false;
end;
end;
exit(false);
end;
//这里是dij的堆优化
procedure up(x:longint);
var
temp:longint;
begin
while (x div 2>0) and (dis[d[x]]<dis[d[x div 2]]) do
begin
bh[d[x]]:=x div 2;
bh[d[x div 2]]:=x;
temp:=d[x];
d[x]:=d[x div 2];
d[x div 2]:=temp;
x:=x div 2;
end;
end;
procedure down(y:longint);
var
temp,x:longint;
begin
x:=1;
while ((x*2<=t) and (dis[d[x]]>dis[d[x*2]])) or ((x*2+1<=t) and (dis[d[x]]>dis[d[x*2+1]])) do
begin
if (x*2+1<=t) and (dis[d[x*2+1]]<dis[d[x*2]]) then
begin
bh[d[x]]:=x*2+1;
bh[d[x*2+1]]:=x;
temp:=d[x];
d[x]:=d[x*2+1];
d[x*2+1]:=temp;
x:=x*2+1;
end
else
begin
bh[d[x]]:=x*2;
bh[d[x*2]]:=x;
temp:=d[x];
d[x]:=d[x*2];
d[x*2]:=temp;
x:=x*2;
end;
end;
end;
begin
//构图过程已略
//最短路求距离标号dis
fillchar(dis,sizeof(dis),127);
maxx:=dis[1];
t:=1;
dis[n+m+2]:=0;
b[n+m+2]:=true;
bh[n+m+2]:=t;
d[t]:=n+m+2;
up(t);
while t>0 do
begin
b[d[1]]:=true;
i:=last[d[1]];
while i>0 do
begin
if (b[tov[i]]=false) and (dis[d[1]]+value[i]<dis[tov[i]]) then
begin
if dis[tov[i]]=maxx then
begin
inc(t);
dis[tov[i]]:=dis[d[1]]+value[i];
bh[tov[i]]:=t;
d[t]:=tov[i];
up(t);
end
else
begin
dis[tov[i]]:=dis[d[1]]+value[i];
up(bh[tov[i]]);
end;
end;
i:=next[i];
end;
bh[d[1]]:=0;
bh[d[t]]:=1;
d[1]:=d[t];
dec(t);
down(t);
end;
//费用流
kp:=now;//当前弧优化
repeat
for i:=1 to en do now[i]:=kp[i];
while flow(1,maxlongint)>0 do//费用流
begin
for i:=1 to en do pd[i]:=false;
end;
//可以在这里动态加边,代码已省略
until change;//change表示改变距离标号
writeln(ans);
end.
放些题目——
T1、【TJOI2014】匹配(match)
题解:水题。
KM或费用流都可做。
主要讲讲费用流。
我们可以从s连n个男孩1流量、0费用。
每个男孩连女孩1流量,hij费用。
每个女孩连t1流量、0费用。
可以考虑zkw+动态加边优化。
T2、【GDOI2016模拟】作业分配
这个也是KM或费用流都可做。
我写了一篇blog来详细解释。
https://blog.csdn.net/hichocolate/article/details/81044164
T3、炼狱 by——zlt
题目主要的部分——
作者说解法为裸的费用流,但,本人太菜,还未想到一个很好的解法。
所以,先放着咯~~~