Description
Input
Output
Sample Input
3 2
7 11
1 5
3 8
4
7
Sample Output
5
Data Constraint
题解
这道题看似很难做。
实际上可以利用一些很简单的计算答案方式来弄。
我就选择了一个比较好理解但实现很难弄的。
~~ 别人打1000Byte,我打6000Byte~~
首先,我们把输入的x[i],y[i],a[i]全部都离散化一下。
然后,把离散完的x[i],y[i]依照x为关键字排序,把a[i]排序。
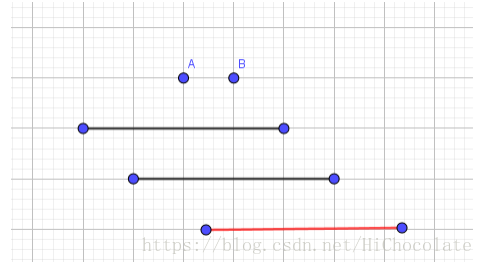
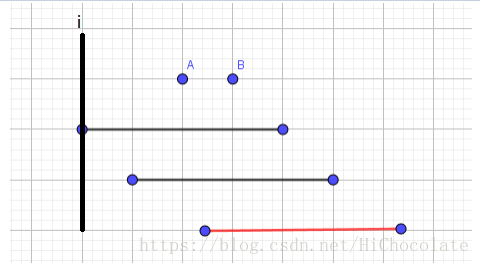
于是乎,建出来的图类似于下面的这个图:
然后,我们就考虑从左边一个i扫过去。
那么我们每次到达一条线段的左端点就把它的右端点加入一个堆中,反之就从堆中删除。
那么我们一旦走到一个安全的地方,就可以直接得出当前这个地方所能挖到的矿。(在堆里)
假设当前到了第k个安全地方,那么它所能够挖的矿物为dk[],总数为gk
之前可以挖到的矿物为dj[]
那么我们发现这两个集合中,dk[]有一些是之前dj[]里有的,一共有cf个重复的矿物。那么计算答案时就不可以算重复。
实际上,答案就是:
这样一来,我们就可以从左边一直扫到右边,同时可以保证答案的正确。
至于怎么算这个重复的矿物。
我们可以对于当前的dk[]中新加入的点都打个k的标记,那么下次维护堆同时利用这个标记来维护cf即可。
const op=100000;
var
ans:int64;
mo:int64=998244353;
i,j,k,l,n,m,tot,last,maxx,st,now,one,two:longint;
x,y:array[1..op] of longint;
a,d,id,ye:array[1..op*2] of longint;
lsh,bh,kind:array[1..3*op] of longint;
mi:array[0..op+1] of int64;
jl:array[1..op] of boolean;
flag:boolean;
procedure up(x:longint);
var
temp:longint;
begin
while (x div 2>0) and (d[x]<d[x div 2]) do
begin
temp:=d[x];
d[x]:=d[x div 2];
d[x div 2]:=temp;
temp:=id[x];
id[x]:=id[x div 2];
id[x div 2]:=temp;
temp:=ye[x];
ye[x]:=ye[x div 2];
ye[x div 2]:=temp;
x:=x div 2;
end;
end;
procedure down(y:longint);
var
temp,x:longint;
begin
x:=1;
while ((x*2<=tot) and (d[x]>d[x*2])) or ((x*2+1<=tot) and (d[x]>d[x*2+1])) do
begin
if (x*2+1<=tot) and (d[x*2+1]<d[x*2]) then
begin
temp:=d[x];
d[x]:=d[x*2+1];
d[x*2+1]:=temp;
temp:=id[x];
id[x]:=id[x*2+1];
id[x*2+1]:=temp;
temp:=ye[x];
ye[x]:=ye[x*2+1];
ye[x*2+1]:=temp;
x:=x*2+1;
end
else
begin
temp:=d[x];
d[x]:=d[x*2];
d[x*2]:=temp;
temp:=ye[x];
ye[x]:=ye[x*2];
ye[x*2]:=temp;
x:=x*2;
end;
end;
end;
procedure qsorta(l,r:longint);
var
i,j,k,m:longint;
begin
i:=l;j:=r;
m:=a[(l+r) div 2];
repeat
while a[i]<m do inc(i);
while a[j]>m do dec(j);
if i<=j then
begin
k:=a[i];
a[i]:=a[j];
a[j]:=k;
inc(i);
dec(j);
end;
until i>j;
if l<j then qsorta(l,j);
if r>i then qsorta(i,r);
end;
procedure qsortw(l,r:longint);
var
i,j,k,m:longint;
begin
i:=l;j:=r;
m:=x[(l+r) div 2];
repeat
while x[i]<m do inc(i);
while x[j]>m do dec(j);
if i<=j then
begin
k:=x[i];
x[i]:=x[j];
x[j]:=k;
k:=y[i];
y[i]:=y[j];
y[j]:=k;
inc(i);
dec(j);
end;
until i>j;
if l<j then qsortw(l,j);
if r>i then qsortw(i,r);
end;
procedure qsort(l,r:longint);
var
i,j,k,m:longint;
begin
i:=l;j:=r;
m:=lsh[(l+r) div 2];
repeat
while lsh[i]<m do inc(i);
while lsh[j]>m do dec(j);
if i<=j then
begin
k:=lsh[i];
lsh[i]:=lsh[j];
lsh[j]:=k;
k:=bh[i];
bh[i]:=bh[j];
bh[j]:=k;
k:=kind[i];
kind[i]:=kind[j];
kind[j]:=k;
inc(i);
dec(j);
end;
until i>j;
if l<j then qsort(l,j);
if r>i then qsort(i,r);
end;
begin
assign(input,'ore.in');reset(input);
assign(output,'ore.out');rewrite(output);
readln(n,m);
for i:=1 to n do
begin
readln(x[i],y[i]);
inc(tot);
lsh[tot]:=x[i];
bh[tot]:=i;
kind[tot]:=1;
inc(tot);
lsh[tot]:=y[i];
bh[tot]:=i;
kind[tot]:=2;
end;
for i:=1 to m do
begin
readln(a[i]);
inc(tot);
lsh[tot]:=a[i];
bh[tot]:=i;
kind[tot]:=3;
end;
qsort(1,tot);
j:=0;
last:=0;
for i:=1 to tot do
begin
if lsh[i]<>last then
begin
inc(j);
last:=lsh[i];
end;
if kind[i]=1 then x[bh[i]]:=j
else if kind[i]=2 then y[bh[i]]:=j
else a[bh[i]]:=j;
end;
qsorta(1,m);
qsortw(1,n);
maxx:=j;
mi[0]:=1;
mi[1]:=2;
for i:=2 to n+1 do
begin
mi[i]:=(mi[i-1]*2) mod mo;
end;
st:=1;
now:=1;
tot:=0;
flag:=true;
for i:=1 to maxx do
begin
while (tot>0) and (d[1]<i) do
begin
if ye[1]<>now then
begin
dec(two);
end;
d[1]:=d[tot];
id[1]:=id[tot];
ye[1]:=ye[tot];
dec(tot);
down(1);
end;
while (st<=n) and (x[st]<=i) do
begin
inc(tot);
d[tot]:=y[st];
id[tot]:=st;
ye[tot]:=now;
inc(st);
up(tot);
end;
if a[now]=i then
begin
begin
one:=tot;
ans:=(ans+(mi[one]-mi[two]+mo) mod mo) mod mo;
two:=tot;
end;
inc(now);
end;
end;
writeln(ans);
end.