Traveler
The famous traveler BaoBao is visiting the Dream Kingdom now. There are n cities in Dream Kingdom, numbered from 1 to n. The cities are connected by directed roads. For all 1≤i≤n:
- There is a road from the i-th city to the (i−1)-th city if 1≤i−1≤n.
- There is a road from the i-th city to the 2i-th city if 1≤2i≤n.
- There is a road from the i-th city to the (2i+1)-th city if 1≤2i+1≤n.
- There is a road from the i-th city to the ⌊2i⌋-th city if 1≤⌊2i⌋≤n, where ⌊2i⌋ indicates the largest integer x such that 2x≤i.
BaoBao starts his travel from the 1st city. As he doesn't like visiting a city more than once, he wants to find a route which goes through each of the n cities exactly once. Can you help him find such a route?
Input
There are multiple test cases. The first line of the input contains an integer T, indicating the number of test cases. For each test case:
The first and the only line contains an integer n (1≤n≤105), indicating the number of cities in Dream Kingdom.
It's guaranteed that the sum of n of all test cases will not exceed 106.
Output
For each test case output one line. If there exists a route which starts from the 1st city and visits each city exactly once, output n integers c1,c2,…,cn separated by a space, where ci indicates the i-th city in the route (note that according to the description, there must be c1=1). If there is no valid route, output "-1" (without quotes) instead. If there are multiple valid answers, you can output any of them.
Please, DO NOT output extra spaces at the end of each line, or your solution may be considered incorrect!
Sample Input
2 2 9
Sample Output
1 2 1 3 6 5 2 4 9 8 7
思路:
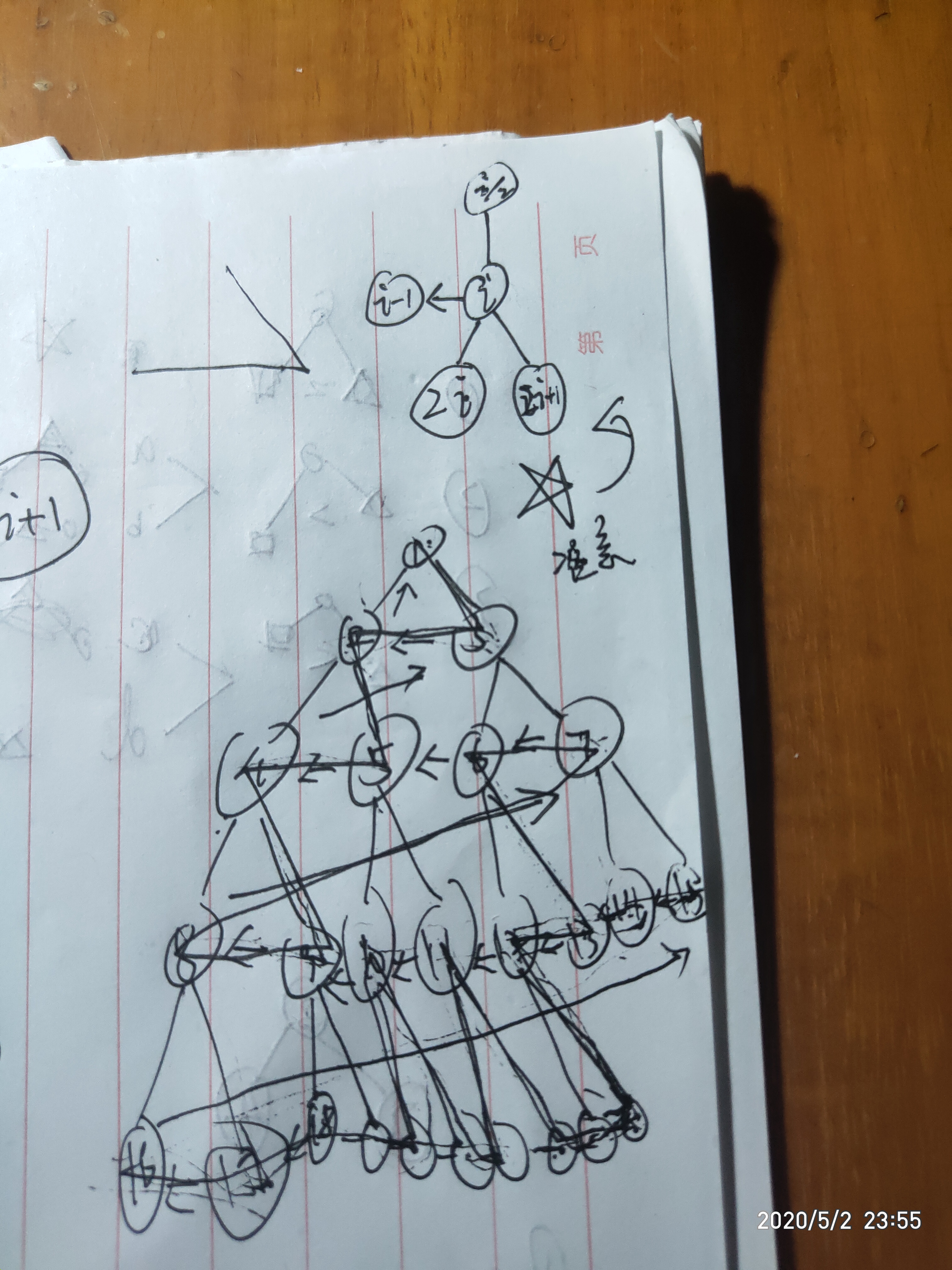
欧拉路径,整体类似一颗有双向边的完全二叉树,但每个u(u>1)都有一条指向u-1的有向边,u<n/2时走一次2*u+1,然后走完u-1,如此循环,当u==n/2之后,按优先级走,优先2*u+1,其次2*u,再次u/2,最次u-1,如此循环,直到走完n个结点
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int amn=1e5+5; 4 int n; 5 int ans[amn],tp; 6 int vis[amn]; 7 void sovle(int u){ 8 int f=0,flag=0; 9 while(tp<n){ 10 vis[u]=1; 11 ans[++tp]=u;//cout<<u<<' '<<f<<' '; 12 if(u>=n/2)flag=1; 13 if(!flag){ 14 if(f==0&&(u<<1|1)<=n&&!vis[u<<1|1]){ 15 f=1; 16 u=(u<<1|1); 17 } 18 else{ 19 f=1; 20 //cout<<vis[u-1]<<' '<<vis[u<<1|1]; 21 if((u-1)>=1&&!vis[u-1]){ 22 f=1; 23 u=u-1; 24 } 25 else if((u<<1|1)<=n&&!vis[u<<1|1]){ 26 f=1; 27 u=(u<<1|1); 28 } 29 } 30 } 31 else{ 32 if((u<<1|1)<=n&&!vis[u<<1|1]){ 33 u=(u<<1|1); 34 } 35 else if((u<<1)<=n&&!vis[u<<1]){ 36 u=(u<<1); 37 } 38 else if((u>>1)>=1&&!vis[u>>1]){ 39 u=(u>>1); 40 } 41 else if((u-1)>=1&&!vis[u-1]){ 42 u=u-1; 43 } 44 } 45 //cout<<endl; 46 } 47 } 48 int main(){ 49 int T;cin>>T; 50 while(T--){ 51 cin>>n; 52 memset(vis,0,sizeof vis); 53 tp=0; 54 sovle(1); 55 for(int i=1;i<=n;i++){ 56 printf("%d%c",ans[i],i<n?' ':' '); 57 } 58 } 59 } 60 /** 61 欧拉路径,整体类似一颗有双向边的完全二叉树,但每个u(u>1)都有一条指向u-1的有向边,u<n/2时走一次2*u+1,然后走完u-1,如此循环,当u==n/2之后,按优先级走,优先2*u+1,其次2*u,再次u/2,最次u-1,如此循环,直到走完n个结点 62 */