[概率] HDU 2019 Multi-University Training Contest 10

Valentine's Day

Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Special Judge

Problem Description

Oipotato loves his girlfriend very much. Since Valentine's Day is coming, he decides to buy some presents for her.

There are

Input

There are multiple test cases. The first line of the input contains an integer

Output

For each test case output one line, indicating the answer. Your answer will be considered correct if and only if the absolute error of your answer is less than

Sample Input

2 3 0.100000 0.200000 0.900000 3 0.100000 0.300000 0.800000

Sample Output

0.900000000000 0.800000000000

题意:

有n种商品，每种商品有pi的概率让女朋友非常开心，现在问买那些商品才能让女朋友恰好非常开心一次的概率最大

思路:

记p为恰好让女朋友非常开心一次的概率,p=Σ(i=1->m)piπ（j=1->m且i!=j)(1-pj),算了一些样例后发现如果pi>0.5，那么无论再买那些商品都会让总概率变小，
如果pi==0.5，则无论再买那些商品都会让总概率=0.5,所以如果存在pi>=0.5，则我们就取一个最大的大于等于0.5概率的商品，否则商品概率都小于0.5时，
队友通过打表发现将商品排序后，从最大的那个开始连续取，总概率会先递增再递减，且只有一个极大值,现在的问题是最坏的情况是要遍历所有商品，复杂度为O(n)
每次都要重新计算总概率，计算总概率的复杂度为O(nn)，所以这样的总复杂度为O(nnn)，而题目中n最大为1e4，显然n的立方的复杂度是不能接受的，
遍历的O(n)没什么办法优化，但我们可以把计算总概率的O(nn)的复杂度降为O(n)，这样O(nn)的复杂度是能支持1e4的数据的，所以现在的问题就是怎么优化计算
原始公式为p=Σ(i=1->m)piπ（j=1->m且i!=j)(1-pj)，可以将其转换为，p=Σ(i=1->m)piπ（j=1->m)(1-pj)/(1-pi),因为π（j=1->m)(1-pj)与i无关，所以可以把他从累加中提出来，
转换为p=[Σ(i=1->m)pi/(1-pi)]*[π（j=1->m)(1-pj)],于是可以O(n)地计算Σ(i=1->m)pi/(1-pi)和π（j=1->m)(1-pj)，最后将两者相乘即为总概率

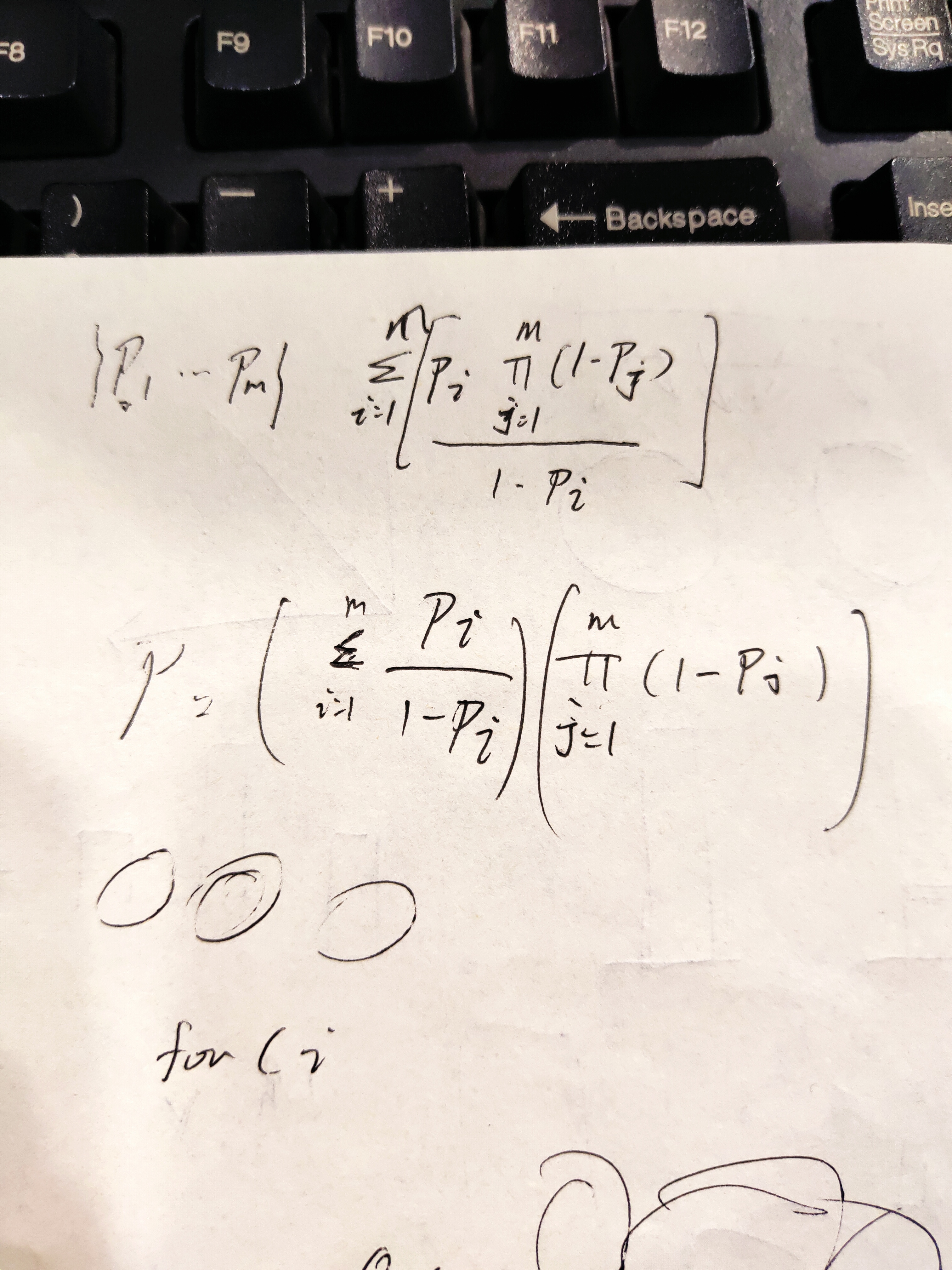
 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int amn=1e4+5;
 4 struct node{
 5     double p,q;
 6 }nm[amn];
 7 double p[amn],q[amn],ans,cnt,maxn,aa,s,t;
 8 bool cmp(node a,node b){
 9     if(a.p==b.p)return a.q<b.q;
10     return a.p>b.p;
11 }
12 int main(){
13     int n,T,tp;
14     ios::sync_with_stdio(0);
15     scanf("%d",&T);
16     while(T--){
17         scanf("%d",&n);
18         tp=maxn=0;
19         aa=1;
20        for(int i=1;i<=n;i++){
21             scanf("%lf",&nm[i].p);
22             maxn=max(maxn,nm[i].p);
23             nm[i].q=1-nm[i].p;
24         }
25         if(maxn>=0.5){
26             ans=maxn;
27         }
28         else{
29             tp=maxn=0;
30             sort(nm+1,nm+1+n,cmp);
31             ans=nm[1].p;
32             for(int i=2;i<=n;i++){
33                 s=0,t=1;
34                 for(int j=1;j<=i;j++)s+=nm[j].p/nm[j].q;
35                 for(int j=1;j<=i;j++)t*=nm[j].q;
36                 if(s*t>ans)
37                     ans=s*t;
38                 else break;
39             }
40         }
41         printf("%.12lf
",ans);
42     }
43 }
44 /**
45 有n种商品，每种商品有pi的概率让女朋友非常开心，现在问买那些商品才能让女朋友恰好非常开心一次的概率最大
46 记p为恰好让女朋友非常开心一次的概率,p=Σ(i=1->m)pi*π（j=1->m且i!=j)(1-pj),算了一些样例后发现如果pi>0.5，那么无论再买那些商品都会让总概率变小，
47 如果pi==0.5，则无论再买那些商品都会让总概率=0.5,所以如果存在pi>=0.5，则我们就取一个最大的大于等于0.5概率的商品，否则商品概率都小于0.5时，
48 队友通过打表发现将商品排序后，从最大的那个开始连续取，总概率会先递增再递减，且只有一个极大值,现在的问题是最坏的情况是要遍历所有商品，复杂度为O(n)
49 每次都要重新计算总概率，计算总概率的复杂度为O(n*n)，所以这样的总复杂度为O(n*n*n)，而题目中n最大为1e4，显然n的立方的复杂度是不能接受的，
50 遍历的O(n)没什么办法优化，但我们可以把计算总概率的O(n*n)的复杂度降为O(n)，这样O(n*n)的复杂度是能支持1e4的数据的，所以现在的问题就是怎么优化计算
51 原始公式为p=Σ(i=1->m)pi*π（j=1->m且i!=j)(1-pj)，可以将其转换为，p=Σ(i=1->m)pi*π（j=1->m)(1-pj)/(1-pi),因为π（j=1->m)(1-pj)与i无关，所以可以把他从累加中提出来，
52 转换为p=[Σ(i=1->m)pi/(1-pi)]*[π（j=1->m)(1-pj)],于是可以O(n)地计算Σ(i=1->m)pi/(1-pi)和π（j=1->m)(1-pj)，最后将两者相乘即为总概率
53 **/

原文地址：https://www.cnblogs.com/Railgun000/p/11390598.html