Codeforces Add on a Tree

Add on a Tree

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Note that this is the first problem of the two similar problems. You can hack this problem only if you solve both problems.

You are given a tree with nn nodes. In the beginning, 00 is written on all edges. In one operation, you can choose any 22 distinct leaves uu, vvand any real number xx and add xx to values written on all edges on the simple path between uu and vv.

For example, on the picture below you can see the result of applying two operations to the graph: adding 22 on the path from 77 to 66, and then adding −0.5−0.5 on the path from 44 to 55.

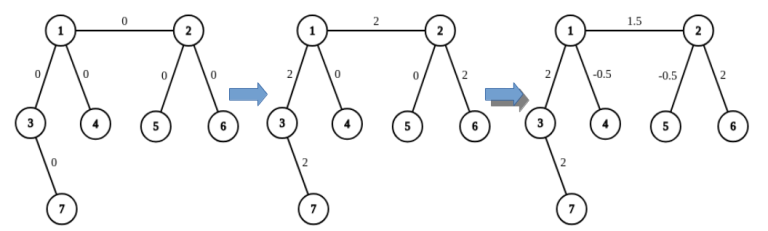
Is it true that for any configuration of real numbers written on edges, we can achieve it with a finite number of operations?

Leaf is a node of a tree of degree 11. Simple path is a path that doesn't contain any node twice.

Input

The first line contains a single integer nn (2≤n≤1052≤n≤105) — the number of nodes.

Each of the next n−1n−1 lines contains two integers uu and vv (1≤u,v≤n1≤u,v≤n, u≠vu≠v), meaning that there is an edge between nodes uu and vv. It is guaranteed that these edges form a tree.

Output

If there is a configuration of real numbers written on edges of the tree that we can't achieve by performing the operations, output "NO".

Otherwise, output "YES".

You can print each letter in any case (upper or lower).

Examples

input

Copy

2
1 2

output

Copy

YES

input

Copy

3
1 2
2 3

output

Copy

NO

input

Copy

5
1 2
1 3
1 4
2 5

output

Copy

NO

input

Copy

6
1 2
1 3
1 4
2 5
2 6

output

Copy

YES

Note

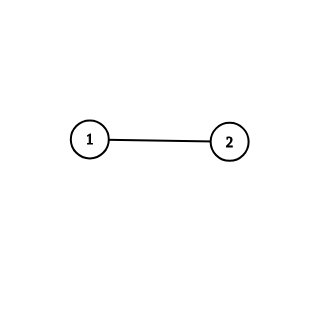
In the first example, we can add any real xx to the value written on the only edge (1,2)(1,2).

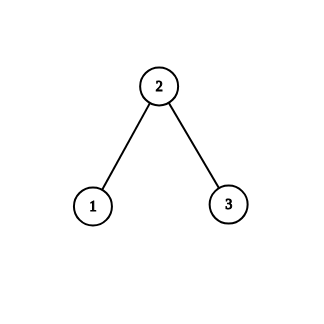
In the second example, one of configurations that we can't reach is 00 written on (1,2)(1,2) and 11 written on (2,3)(2,3).

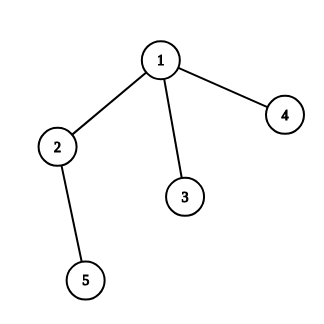
Below you can see graphs from examples 33, 44:

题意:给一颗n个节点边权都为0的树，现在有一种操作可以任意选择这颗树上的两个叶子节点（度数为1的节点）使得这两个节点简单路径(没有重复节点的路径)上的边权加上一个任意实数，
问给定节点的连接关系形成一颗树，能否有限次使用上述操作使得树上的边权可以为任意实数（可能每一条边都不一样）
思路:样例2表明，如果存在一个节点恰好只连接了两个节点，则其只连了两条边，形成一条链，则条链必定会在两个根节点的简单路径上，而简单路径上的边权是同时加一个实数的，所以这个节点的两条边必定同时加一个实数且两条边的值必定相同
故这两条边无法在有限次操作内到达权值不同的情况，应输出NO，其他情况都可以通过某些边加上一些值，某些边减去一些值得到，输出YES

#include<bits/stdc++.h>
using namespace std;
const int amn=1e5+5;
vector<int> a[amn];
int main(){
    int n,f=1,u,v;
    cin>>n;
    for(int i=1;i<n;i++){
        cin>>u>>v;
        a[u].push_back(v);
        a[v].push_back(u);
    }
    for(int i=1;i<=n;i++){
        if(a[i].size()==2){ ///若存在一个点度数为2，则输出NO
            f=0;
            break;
        }
    }
    if(f)printf("YES
");   ///否则输出YES
    else printf("NO
");
}
/***
给一颗n个节点边权都为0的树，现在有一种操作可以任意选择这颗树上的两个叶子节点（度数为1的节点）使得这两个节点简单路径(没有重复节点的路径)上的边权加上一个任意实数，
问给定节点的连接关系形成一颗树，能否有限次使用上述操作使得树上的边权可以为任意实数（可能每一条边都不一样）
样例2表明，如果存在一个节点恰好只连接了两个节点，则其只连了两条边，形成一条链，则条链必定会在两个根节点的简单路径上，而简单路径上的边权是同时加一个实数的，所以这个节点的两条边必定同时加一个实数且两条边的值必定相同
故这两条边无法在有限次操作内到达权值不同的情况，应输出NO，其他情况都可以通过某些边加上一些值，某些边减去一些值得到，输出YES
***/