[USACO13FEB] 出租车Taxi
题意:
长度为M的栅栏上,有N(1 <= N <= 100,000)头牛需要坐车前往别的地方,起点和终点分别为Ai和Bi。现在一辆出租车从最左端0出发,要运送完所有牛,最后到达最右端M(1 <= M <= 1,000,000,000),求最小路程。
出租车只能一次载一只牛。奶牛可以在同一时刻完成上车和下车。
输入
第1行:输入N和M;
第2~N+1行:每行2个数,第i+1行,表示第i头牛起点Ai和终点Bi (0≤Ai, Bi≤M)
2 10
0 9
6 5
12
首先,这是一道妙题。(笔者“妙题”的定义 是 自己想不出来的题)
同桌在写这道题,我就跟了一波风。他说,这题很暴力的写就行了。
看了题,我的第一反应是,噢~差不多知道怎么写DP了。
然后我就这么说了,一波群嘲,被告知贪心就可以了。贪心?...我开始了苦想贪心的过程...
最终...看了题解...
思路:
1. 总路程=载牛路程+空载路程
(1) 由于 一次只能载一只牛 且 不走回头路(从Ai直达Bi) 保证了 载牛路程min= ∑ abs(Ai-Bi)
(2) 回头次数min 且 回头距离min 保证了 空载路程min
- 什么时候会空载?
当从初始点(Ai)运送"一个"奶牛的途中,遇到了 第一个(最近的) 目的点——
此时的目的点有两种情况。
a. 这个目的点 是 "另一个"奶牛的目的点(Bj) :
此时,由于一次只能载一只牛,为了答案更优,需在此(Bj)放下这"一个"奶牛,而载上"另一个"奶牛,先送"另一个"去目的点(Bj)。由于第(1)步里,我们已经算了每个奶牛从起始点到目的点的距离和,所以已经加过"另一个"奶牛从起始点(Aj)到目的点(Bj)的距离。
所以,我们只需加上 "另一个"的目的点(Bj) 返回 放下那"一个"的原地点(Aj)的路程 =回头路=空载路
b. 这个目的点 就是 这"一个" 的目的点 (Bi)。
显然,将这"一个"送达目的点后 到 "另一个"(下一个)奶牛的起始点之间也是空载路
c. 注意: 从0到m,首尾是有两段空载路的。
- 说到首尾,有一种巧妙的处理方法 (咕咕咕)
1 #include<cstdio> 2 #include<algorithm> 3 #define N 100010 4 using namespace std; 5 int read(){ 6 int x=0,f=1; char c=getchar(); 7 while(c<'0'||c>'9') {if(c=='-') f=-1; c=getchar();} 8 while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar(); 9 return x*f; 10 } 11 int n,m; 12 long long ans; 13 int a[N],b[N]; 14 int main() 15 { 16 n=read(),m=read(); 17 for(int i=1;i<=n;i++){ 18 a[i]=read(),b[i]=read(); 19 ans+=abs(a[i]-b[i]); 20 } 21 n+=1; 22 a[n]=m,b[n]=0; 23 sort(a+1,a+1+n); 24 sort(b+1,b+1+n); 25 for(int i=1;i<=n;i++) 26 ans+=abs(a[i]-b[i]); 27 printf("%lld",ans); 28 return 0; 29 }
P2512 [HAOI2008]糖果传递
题意:有n个小朋友坐成一圈,每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为1。
求使所有人获得均等糖果的最小代价。
思路:
1. 初始 a [ i ] 颗糖果,X [ i ] 表示第i个小朋友给了第i-1个小朋友Xi颗糖果。 如果Xi<0,说明第i-1个小朋友给了第i个小朋友Xi颗糖果,X1表示第一个小朋友给第n个小朋友的糖果数量。
所以最后的答案就是 ans= |X1| + |X2| + |X3| + ……+ |Xn|。
对于第一个小朋友,他给了第n个小朋友X1颗糖果,还剩a1-X1颗糖果,但因为第2个小朋友给了他X2颗糖果,所以最后还剩a1-X1+X2颗糖果。根据题意,最后的糖果数量等于average,即得到了一个方程:a1-X1+X2=average。
同理,对第二个人有 a2-x2+x3=average。于是我们可以得到n个方程,共n个变量。
但我们却不能直接解方程。因为从前n-1个方程可以推出最后一个。实际上有用的只有n-1个。
对于第1个小朋友,a1-X1+X2=average -> X2=average-a1+X1 = X1 - b1 (假设 b1=a1-average,下面类似)
对于第2个小朋友,a2-X2+X3=average -> X3=average-a2+X2 = 2*average-a1-a2+X1 = X1- b2 ( b2=a1+a2-2*average)
对于第3个小朋友,a3-X3+X4=average -> X4=average-a3+X3 = 3*average-a1-a2-a3+X1 = X1- b3
......
对于第n个小朋友,an-Xn+X1=average
由于可以用X1表示出其他的Xi,那么本题就变成了单变量的极值问题。
2. 我们希望Xi的绝对值之和尽量小,即|X1| + |X1-C1| + |X1-C2| + ……+ |X1-Cn-1|要尽量小。
注意到 |X1-Ci| 的几何意义是数轴上的点X1到Ci的距离,所以问题变成了:给定数轴上的n个点,找出一个到他们的距离之和尽量小的点。
不难猜到,最优的 Xi 就是这些数中的中位数。
接下来,我们证明:
数轴上n个点,中位数到各点的距离之和最小。
Eg: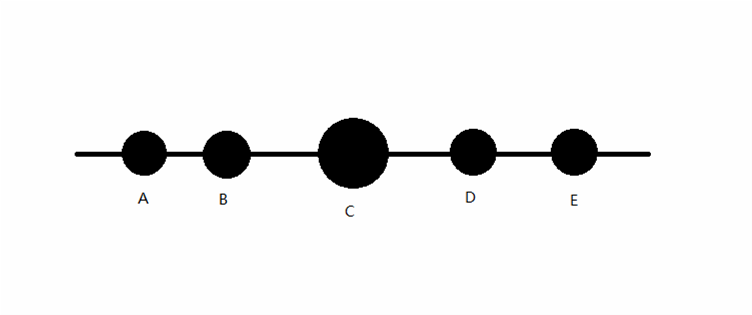
1 #include<cstdio> 2 #include<algorithm> 3 #define ll long long 4 using namespace std; 5 int read() 6 { 7 int x=0,f=1; char c=getchar(); 8 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} 9 while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar(); 10 return x*f; 11 } 12 ll n,mid,sum,ans,average; //注意 long long 13 int a[1000010],b[1000010]; 14 int main() 15 { 16 n=read(); 17 for(int i=1;i<=n;i++){ 18 a[i]=read(); 19 sum+=a[i]; 20 21 } 22 average=sum/n; 23 for(int i=1;i<=n;i++) b[i]=b[i-1]+a[i]-average; 24 sort(b+1,b+1+n); 25 mid=b[(n+1)/2]; 26 for(int i=1;i<=n;i++) 27 ans+=abs(mid-b[i]); 28 printf("%lld",ans); 29 return 0; 30 }
P3049 [USACO12MAR]园林绿化Landscaping
题目描述
有几个选择:购买一块的土,并将它放在他选择的花圃中, 花费X单位的钱。
清除一块泥土,花费Y单位的钱。
请计算农民约翰完成他的绿化项目的最低总成本。
FA 1 DP ( 两边似乎还有些问题,咕一下...)
思路:
1. 把输入的初始数组和目标数组转化成如下格式:
a 2 3 4 5
a' 1 1 2 2 2 3 3 3 3 4 4 4 4 4
b 3 1 5 2
b' 1 1 1 2 3 3 3 3 3 4 4
2. f [ i ][ j ] 中 i 表示运走土块数, j 表示购买土块数
code:
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,x,y,z,a[1010],b[1010],f[1010][1010],p,q; 4 int minx(int a,int b,int c) 5 { 6 if(a<=b &&a<=c)return a; 7 if(b<=a &&b<=c)return b; 8 if(c<=a &&c<=b)return c; 9 } 10 11 int main() 12 { 13 int lena=0,lenb=0; 14 cin>>n>>x>>y>>z; 15 for(int i=1;i<=n;i++){ 16 cin>>p>>q; 17 for(int j=1;j<=p;j++)a[++lena]=i; 18 for(int k=1;k<=q;k++)b[++lenb]=i; 19 } 20 f[0][0]=0; //极限情况作为边界 21 for(int i=1;i<=lena;i++)f[i][0]=i*y; 22 for(int i=1;i<=lenb;i++)f[0][i]=i*x; 23 24 for(int i=1;i<=lena;i++){ 25 for(int j=1;j<=lenb;j++){ 26 f[i][j]=minx(f[i-1][j]+y,f[i][j-1]+x,f[i-1][j-1]+z*abs(a[i]-b[j])); 27 } 28 } 29 cout<<f[lena][lenb]<<endl; 30 return 0; 31 }
FA 2 堆贪心