py二叉树si种遍历及常见面试总结

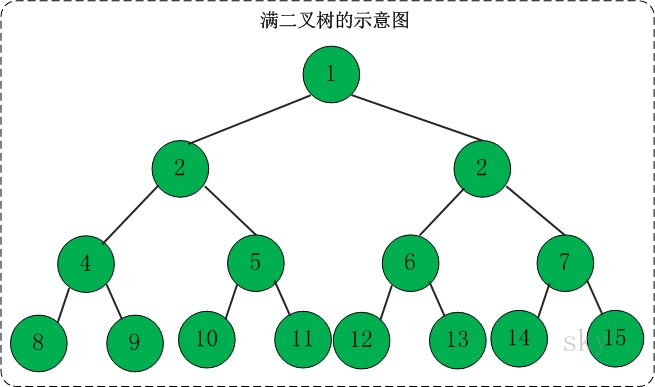
1.二叉树的定义:

二叉树是有限个元素的集合，该集合或者为空、或者有一个称为根节点（root）的元素及两个互不相交的、分别被称为左子树和右子树的二叉树组成。

2.二叉树的常用性质

<1>.二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

<2>.在二叉树的第i层上最多有2 ^i-1 个节点 。（i>=1）

<3>.二叉树中如果深度为k(有k层),那么最多有2^k-1个节点。(k>=1）

<4>.若二叉树按照从上到下从左到右依次编号，则若某节点编号为k，则其左右子树根节点编号分别为2k和2k+1;

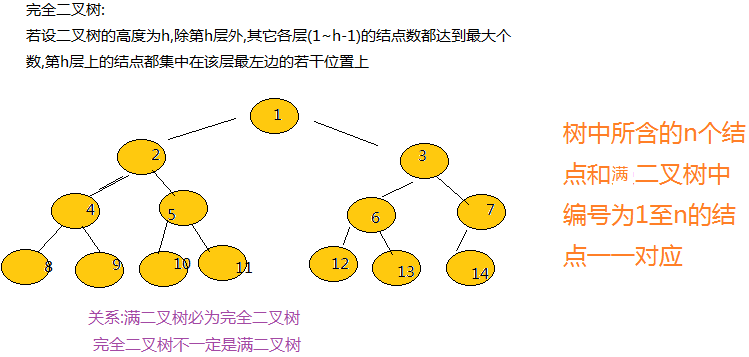
2.二叉树分类：满二叉树，完全二叉树

<1>.满二叉树：高度为h，由2^h-1个节点构成的二叉树称为满二叉树。

<2>.在完全二叉树中，具有n个节点的完全二叉树的深度为[log₂n]+1，其中[log₂n]+1是向下取整。满二叉树的深度为k=log₂(n+1);

3.二叉树的遍历方法:前序遍历/中序遍历/后序遍历 /层序遍历

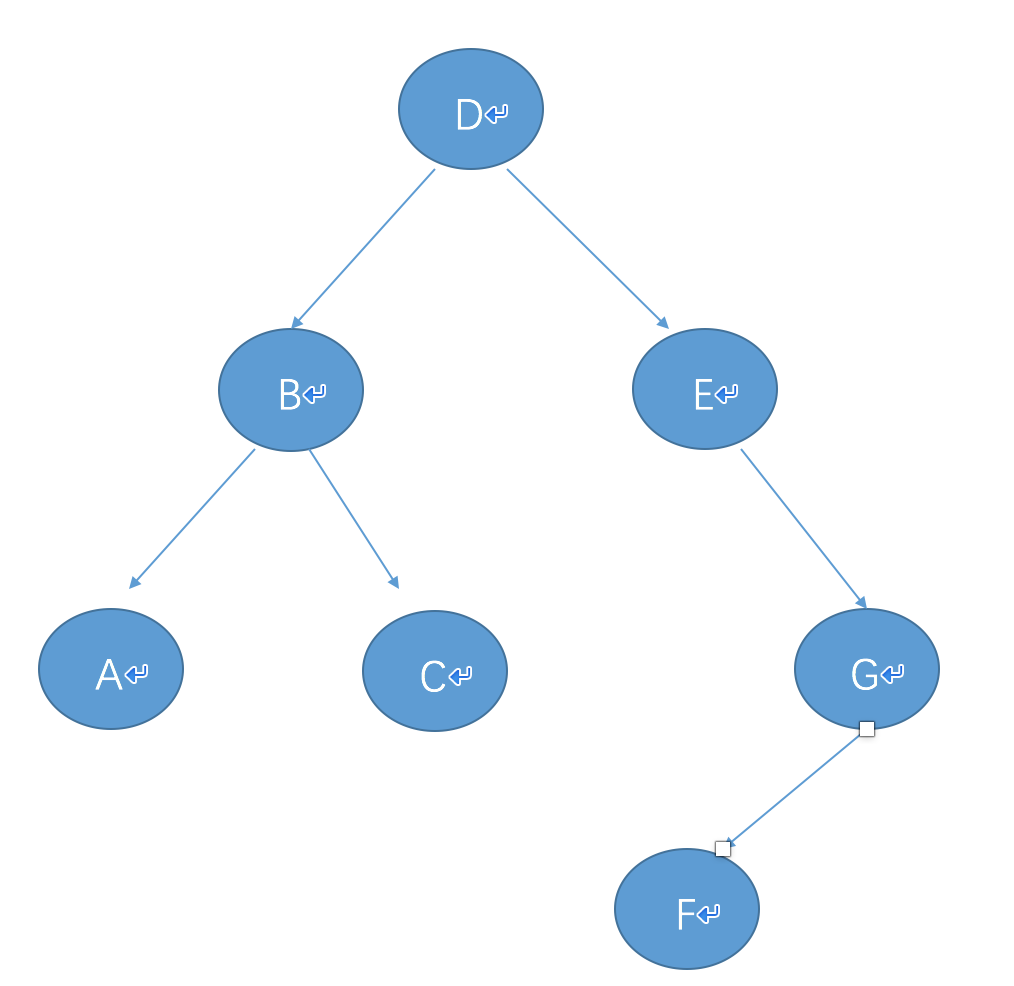
<1>.前序遍历:（1）访问根结点（2）前序遍历全部左子树（3）前序遍历全部右子树 ,如1.<1>图 排序DBACEGF

<2>.中序遍历:（1）中序遍历左子树（2）访问根结点（3）中序遍历右子树,如1.<1>图 排序ABCDEFG

<3>.后序遍历:（1）后序遍历左子树（2）后序遍历右子树（3）访问根结点如1.<1>图排序 ACBFGED

4.py上代码：

class Node:  
     def __init__(self,value=None,left=None,right=None):  
         self.value=value  
         self.left=left    #左子树
         self.right=right  #右子树

def preTraverse(root): 

　　'''
　　前序遍历
　　'''

　　if root==None:
　　　　return
　　print(root.value)
　　preTraverse(root.left)
　　preTraverse(root.right)

　def midTraverse(root):
　　'''
　　中序遍历
　　'''
　　if root==None:
　　　　return
　　midTraverse(root.left)
　　print(root.value)
　　midTraverse(root.right)

　def afterTraverse(root):
　　'''
　　后序遍历
　　'''
　　if root==None:
　　　　return
　　afterTraverse(root.left)
　　afterTraverse(root.right)
　　print(root.value)

if __name__=='__main__':
　　root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
　　print('前序遍历：')
　　preTraverse(root)
　　print(' ')
　　print('中序遍历：')
　　midTraverse(root)
　　print(' ')
　　print('后序遍历：')
　　afterTraverse(root)
　　print(' ')

 　　#输出结果如3.

5.    面试题：已知一棵二叉树的先序遍历为1、2、4、7、3、5、6、8，中序遍历序列为4、7、2、1、5、3、8、6，画出该二叉树

       分析：已知一棵二叉树的先序遍历和中序遍历或者已知一棵二叉树的中序和后序遍历可以画出该二叉树，但是已知一棵二叉树的先序和后序无法确认一棵二叉树。根据先序的从前往后查找确定根节点，根据中序确定根节点的左右子树。由二叉树的先序序列可知，二叉树的根节点为1，由中序遍历可知根节点把二叉树分成两个部分，4、7、2为根节点1的左子树节点，5、3、8、6为根节点1的右子树节点；先序第二个节点2将节点1的左子树4、7、2分成两个部分，4、7为节点2的左子树节点，节点2的右子树为空；同样先序第三个节点4将节点2的左子树4、7分成两个部分，节点4的左子树为空，右子树为7，7的左右子树都为空。同上，3将节点1的右子树5、3、8、6分成两个部分，节点3的左子树为5，右子树由8，6两个节点，节点5的左右子树为空，6将节点3的右子树分成两个部分，节点6左子树为8，右子树为空；

      拓展：同样我们也可以根据中序和后序遍历画出二叉树，根据后序确定根节点，根据中序确定根节点的左右子树，不过此时，我们确定根节点需要从后序的后面往前查找根节点。