正题
题目链接:https://www.luogu.com.cn/problem/P8215
题目大意
有\(2\times n\)个人,第\(2\times i-1\)和第\(2\times i\)个人一组,然后每个人可以选择愿不愿意合作,愿意需要付出\(c_i\)代价,不愿意是\(d_i\)代价,如果两个人都愿意,可以选择合作。如果一个人选择愿意另一个人不愿意,那么愿意的那个人会产生\(e_i\)的代价。
然后给出\(m\)对关系,然后题目描述开摆了

\(1\leq n\leq 5000,0\leq m\leq 10000,1\leq a_i,b_i,c_i,d_i,e_i\leq 10^9\)
解题思路
首先考虑\(c,d,e\)的贡献,考虑用最小割。
首先\(c,d\)要选一个,所以它们肯定是串在一个点上的,所以\(S\rightarrow i\rightarrow T\),\(S\)到\(i\)的流量为\(c\),\(i\)到\(T\)的流量为\(d\)。
然后\(e\)的贡献就是一个选\(c\)一个选\(d\)时的贡献,所以我们可以让\(i\)连向它的队友,流量为\(e\),如果\(i\)选了\(c\),它队友选了\(d\),那么这条\(e\)的边也要割。
然后因为还有一个选择是否合作,但是要求所有的都选择\(c\)的贡献,所以我们让新建一个点\(W\),\(S\rightarrow W\)的一条边表示是否合作(如果连了就表示合作),然后\(W\)连向同一个队的两个点,
那么一个小组的图大概就长这样

然后考虑后面的贡献就很麻烦了

这一个我们可以直接让\(B\)所在组的\(W\)点连接\(A\)点就行了,如果\(A\)选了\(d\)且\(B\)的合作边没被割掉,那么刚好这条路就是通的,也需要被割掉。
至于
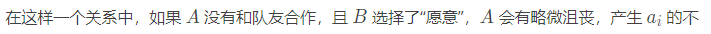
这个贡献,我们考虑反过来处理。
我们发现\(S\rightarrow W_i\)这条边还没有权值,我们可以先默认如果\(A\)没有合作就会产生\(a_i\)的代价,然后如果\(B\)选择了不愿意,那么就会少产生\(a_i\)的贡献,我们让\(B\)的\(d\)值减去\(a_i\)。
然后发现如果此时\(A\)没有合但是\(B\)不愿意也会少产生这个贡献,我们让\(W_A\)连向\(B\)费用为\(a_i\),这样这种情况就不会少算了。
然后因为\(d\)可能减到负数,我们可以让所有的\(c\)和\(d\)加上一个大整数,然后最后统一减去这部分贡献就好了。
这样就完美处理完了所有的条件
code
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define ll long long
using namespace std;
const ll N=5100*6;
struct node{
ll to,next,w;
}a[N<<4];
ll n,m,s,t,c[N],d[N],e[N],w[N];
ll tot=1,ls[N],dep[N],ans;
queue<ll> q;
void addl(ll x,ll y,ll w){
a[++tot].to=y;a[tot].next=ls[x];ls[x]=tot;a[tot].w=w;
a[++tot].to=x;a[tot].next=ls[y];ls[y]=tot;a[tot].w=0;
return;
}
bool bfs(){
while(!q.empty())q.pop();
memset(dep,0,sizeof(dep));
dep[s]=1;q.push(s);
while(!q.empty()){
ll x=q.front();q.pop();
for(ll i=ls[x];i;i=a[i].next){
ll y=a[i].to;
if(!a[i].w||dep[y])continue;
dep[y]=dep[x]+1;
if(y==t)return 1;
q.push(y);
}
}
return 0;
}
ll dinic(ll x,ll flow){
ll rest=0,k;
if(x==t)return flow;
for(ll i=ls[x];i;i=a[i].next){
ll y=a[i].to;
if(!a[i].w||dep[y]!=dep[x]+1)continue;
rest+=(k=dinic(y,min(flow-rest,a[i].w)));
a[i].w-=k;a[i^1].w+=k;
if(rest==flow)return flow;
}
if(!rest)dep[x]=0;
return rest;
}
signed main()
{
scanf("%lld%lld",&n,&m);s=3*n+1;t=s+1;
for(ll i=1;i<=2*n;i++)
scanf("%lld%lld%lld",&c[i],&d[i],&e[i]);
for(ll i=1,x,y,a,b;i<=m;i++){
scanf("%lld%lld%lld%lld",&x,&y,&a,&b);
ll A=(x+1)/2,B=(y+1)/2;
addl(2*n+B,x,b);
w[A]+=a;d[y]-=a;
addl(2*n+A,y,a);
}
for(ll i=1;i<=2*n;i++){
addl(s,i,d[i]+1e14);
addl(i,t,c[i]+1e14);
ll p=(i&1)?(i+1):(i-1);
addl(i,p,e[i]);
}
for(ll i=1;i<=n;i++){
addl(s,2*n+i,w[i]);
addl(2*n+i,2*i-1,1e18);
addl(2*n+i,2*i,1e18);
}
while(bfs())
ans+=dinic(s,1e18);
printf("%lld\n",ans-200000000000000ll*n);
return 0;
}